2.2 Нагрузки

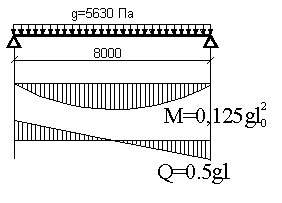
Рисунок 2.3 – К расчёту нагрузок

Расчётная нагрузка на 1 м при ширине плиты 1,2 м с учётом коэффициента надёжности по назначению здания γ_n=0,95

Постоянная g=5,63·1,2·0,95=6,42 кН/м

Полная g+p=18,83·1,2·0,95=21,47 кН/м

Нормативная:

Постоянная g=4,35·1,2·0,95=4,96 кН/м

Полная g+u=15,35·1,2·0,95=17,5 Н/м

Постоянная и длительная полезная 12,05·1,2·0,95=13,74 Н/м

2.3 Усилия от расчетных и нормативных нагрузок

От расчетной нагрузки:

От нормативной нагрузки:

От нормативной постоянной и длительной нагрузки:

2.4 Компоновка поперечного сечения плиты

Высота сечения ребристой предварительно напряженной плиты , округляем в большую сторону

Рабочая высота сечения

Ширина панели по низу

Ширина панели по верху .

Ширина полки

Ширина продольных ребер внизу 70 мм.

В расчетах по предельным состояниям первой группы расчетная толщина сжатой полки таврового сечения ; отношение при этом в расчет вводится вся ширина полки .

Расчетная ширина ребра

Рисунок 2.4 - Поперечные сечения ребристой плиты

а) основные размеры;

б) к расчету прочности;

2.5 Расчёт полки на местный изгиб

Расчётный пролёт при ширине рёбер вверху 8 см составит

ℓ₀=1150-80∙2=990 мм

Нагрузка на 1 м² полки может быть принята (с незначительным превышением) такой же, как и для плиты:

q=(g+u)γ_n=18,83*0,95=17,89 кН/м²

Изгибающий момент для полосы шириной 1 м.

М= кНм

Рабочая высота сечения h₀=5-1,5=3,5 см

А₀=

Из таблицы находим η=0,955

А_s= см²

Принимаем сетку с поперечной арматурой 8Ø6 А-I А=2,26 см² с шагом 110 мм.

2.6 Расчёт прочности сечений нормальных к продольной оси

Расчётный момент от полной нагрузки М=167,5 кНм

А₀=

Из таблицы находим η=0,957 и ζ=х/h₀=0,086

х=ζ*h₀=0,086·37=3,187<h_f'=5 см → нейтральная ось проходит в пределах сжатой полки

Вычисляем характеристики сжатой зоны

ω=0,85-0,008·R_b=0,85-0,008·17·0,9=0,7276

Вычисляем граничную высоту сжатой зоны

ξ_R=

где σ_SR=R_s+400- σ_sp2

σ_SP=0,6R_sn=0,6·590=354 МПа

σ_SP2=γ_sp· σ_SP·0,7=0,84·354·0,7=208,15 МПа

σ_SR=510+400-208,15=701,85 МПа

Проверяем условие 0,3R_s+p< σ_sp<R_s-p

p= МПа

0,3·510+75=228<354<510-75=435→условие выполняется

σ_sр+p=354+75=429<R_sn=590 мПа

Вычисляем предельное отклонение предварительного напряжения

∆γ_sp=

где n_p- число напрягаемых стержней

γ_sp=1-∆γ_sp=1-0,18=0,82

Предварительное напряжение с учётом точности натяжения

σ_sр=0,82·354=290,3 мПа

Предварительное напряжение с учётом полных потерь предварительно принять равным:

σ_sр2=0,7·290,3=203,2 мПа

Определяем коэффициент условия работы с учётом сопротивления напрягаемой арматуры

γ_S6=

где η- условный предел текучести для арматуры класса А IV равный 1,2

γ_S6> η → поэтому принимаем γ_S6=1,2

Находим площадь арматуры

А_s= см²

Принимаем 2Ø25 A IV Аs=9,82 см²

2.7 Расчёт прочности по наклонным сечениям

Поперечная сила от полной нагрузки Q=84,81 кН

Определяем значение продольной силы

N=P= σ_sр2·A_s=203,2·9,82·100=199542 Н

φ_n= <0,5

φ_n- коэффициент учитывающий влияние продольных сил

Принимаем φ_n=0,321

φ_f= <0,5,

где

Принимаем φ_f=0,22

1+ φ_n+ φ_f ≤1,5

1+0,22+0,321=1,542<1,5

Принимаем 1,5

Q_b=Q_sw= кН

Вычисляем проекцию расчётного наклонного сечения

с= >2h₀=74

Принимаем с=74 см тогда

Q_b= Н

93,24>42,405 → поперечная арматура по расчёту не требуется

На приопорных участках ℓ/4=287,5 см устанавливаем конструктивно Ø6 A-I с шагом S=h/2=40/2=20 см

В середине пролёта с шагом 3h/4=3·40/4=30 см