
3.6.4. Метод розгалуджень (комбінаторний метод).
Припущення, що змінна може приймати лише цілочислені значення (у практичному застосуванні найчастіше кінечне число значень), дає змогу розв’язати задачу перевірочною підстановкою усіх допустимих значень в цільову фукцію і порівівнянням отриманих результатів. Однак, зручною для використання ця ідея стає лише тоді, коли повний перебір може бути скоречений додатковими умовами. Ці умови основані на принципі розгалудження комбінаторного програмування. Для розв’язку загальноїцілочислової або змішано-цілочислової задачі лінійного програмування виникає, таким чином, наступний метод.
Для оцінки цільової функції на деякій множині допустимих розв’язків цілочислової задачі служить оптимальний розв’язок відповідної ЗЛП. Множина допустимих розв’язків поступово поділяється, в міру того, як для оптимального плану з нецілочисленими βj = [βj] + {βj} формуються дві задачі з умовами хj ≤ [βj], та хj ≥ [βj] +1. Допустимі області обох задач, об’єднані разом, містять тоді всі допустимі розв’язки цілочислової задачі лінійного програмування.
Розглянемо алгоритм методу розгалуджень:
Симплексним методом розв’язують «послаблену» задачу (3.19) - (3.21) (без виконання вимоги цілочисловості змінних).
Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей розв’язок є оптимальним планом задачі цілочислового програмування (3.19) - (3.21).
Якщо «послаблена» задача (3.19) - (3.21) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то відповідна цілочислова задача(3.19) - (3.21) також не має розв’язку.
Якщо в умовно-оптимальному плані є дробові значення, то вибирають одну з нецілочислових змінних
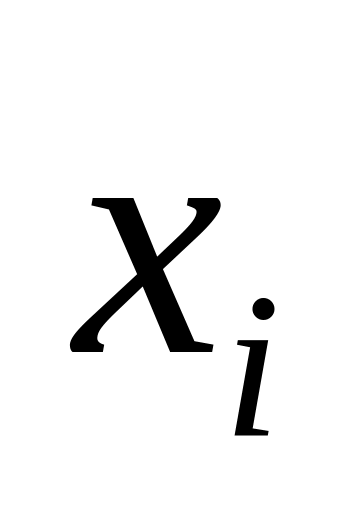 і визначають її цілу частину [βі].
і визначають її цілу частину [βі].Записують два обмеження, що відтинають нецілочислові розв’язки:
xj ≤ [βj], (3.27)
хj ≥ [βj] +1 (3.28)
Кожну з одержаних нерівностей приєднують до обмежень початкової задачі. В результаті отримують дві нові цілочислові задачі лінійного програмування.
Це означає, що симплекс-методом розв’язуються дві задачі:
задача І задача ІІ
|
|
|
|
( |
; — цілі числа, ( ) |
|
|
де βі — не цілочислова компонента розв’язку задачі (3.19)—(3.21).
Розв’язують обидві задачі. Якщо отримано цілочисловий розв’язок хоча б однієї з двох задач, значення цільової функції цієї задачі порівнюють із значенням цільової функції оптимального плану послабленої задачі. Якщо різниця не більша від наперед заданого числа , то процес розв’язування може бути закінчено. У разі, коли цілочисловий розв’язок одержано в обох задачах, то з роз’язком початкової зіставляється той, який дає краще значення цільової функції. Якщо ж в обох задачах одержано нецілочислові розв’язки, то для дальшого розгалудження вибирають ту задачу, для якої значення цільової функції оптимальніше (більше для задачі на maxZ, менше для задачі на minZ )і здійснюють перехід до кроку 2.
Наступне розгалудження виконується доти, доки не буде отримано цілочислений оптимальний розв’язок, або з’ясовано, що цілочисленого оптимального роз’язку не існує. [27].
Приклад 3.6. Розв’язати задачу цілочислового лінійного програмування методом розгалуджень:
![]() ,
,
![]() ;
;
Розв’язок: розв’язуємо «послаблену» задачу, без урахування умови цілочисловості. Остання симплексна таблиця з умовно-оптимальним планом має вигляд:
Хбаз |
Сбаз |
План |
350 |
150 |
0 |
0 |
х1 |
х2 |
х3 |
х4 |
|||
х1 |
350 |
1 |
1 |
0 |
|
|
х2 |
150 |
|
0 |
1 |
|
|
|
1475 |
0 |
0 |
10 |
|
|
Значення змінної х2
не задовольняє умову цілочисленості,
тоді у відповідності до алгоритму,
допустиме ціле значення х2
має задовольняти одну з нерівностей
![]() або
або
![]() .
Формуємо дві задачі, приєднавши до
початкової задачі кожне з обмежень
(3.27) – (3.28), нехтуючи умовою цілочисловості,
і розв’язуємо окремо обидві утворені
задачі:
.
Формуємо дві задачі, приєднавши до
початкової задачі кожне з обмежень
(3.27) – (3.28), нехтуючи умовою цілочисловості,
і розв’язуємо окремо обидві утворені
задачі:
Задача І |
Задача ІІ |
, |
, |
|
; |
|
; |
|
|
|
; |
|
і — цілі числа. |
Для задачі І оптимальним буде
розв’язок
![]() ,
Zmax =
1470, а для задачі ІІ:
,
Zmax =
1470, а для задачі ІІ:
![]() ,
Zmax =
1462,5. Отриманий розв’язок не цілочисловтий,
тому процес розгалудження необхідно
продовжити, на основі першої задачі,
оптимальний план якої дає більше значення
цільової функції. Розв’язуємо задачу
І, приєднавши до неї обмеження:
,
Zmax =
1462,5. Отриманий розв’язок не цілочисловтий,
тому процес розгалудження необхідно
продовжити, на основі першої задачі,
оптимальний план якої дає більше значення
цільової функції. Розв’язуємо задачу
І, приєднавши до неї обмеження:
![]() і
і
![]() .
Отримуємо такі дві задачі:
.
Отримуємо такі дві задачі:
Задача ІІІ |
Задача ІV |
, |
, |
; |
; |
; |
; |
; |
|
; |
; |
|
; |
і — цілі числа. |
і — цілі числа. |
Розв’язком задачі ІІІ є план X*=(x1= 1; x2= 7), Zmax = 1400, а задачі IV план X* = (x1= 2; x2= 5), Zmax = 1450. Обидва розв’язки є цілочисловими, проте краще значення цільової функції забезпечує розв’язок задачі IV. Тому оптимальним розв’язком цілочислової задачі буде оптимальний план IV задачі.
Розв’язування цілочислових задач методом розгалуджень можна значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі розв’язування відрізняється від попередньої лише одним обмеженням. Тому немає сенсу розв’язувати їх симплексним методом спочатку. Достатньо по черзі приєднувати нові обмеження виду (3.27) і (3.28) до останньої симплекс-таблиці попередньої задачі та вилучати (в разі необхідності) непотрібні «старі» обмеження.
