1.1.5. Узагальнення поняття ентропії

Поняття ентропії Больцмана та Гіббса характеризують статистичний підхід до опису системи частинок, так що мікроскопічний стан системи характеризується набором координат та імпульсів частинок, які її складають. Виявляється, що це поняття можна узагальнити на випадок статистичного ансамблю будь-якої фізичної природи.

1.1.5.1. Ентропія Шеннона

Розглянемо тепер довільний статистичний ансамбль, стан якого характеризується деяким набором змінних . Нехай ці змінні характеризуються функцією розподілу , яка задовольняє умові нормування (1.1.22).

Величина

(1.1.30)

називається ентропією Шеннона (в одиницях ). Ентропія Шеннона вступає узагальненням поняття ентропії на статистичні ансамблі довільної природи. Вона може розглядатися як міра невизначеності при статистичному описі.

З визначення ентропії Шеннона зрозуміло, що при розгляді ансамблю частинок вона зводиться до ентропії Гіббса.

1.1.5.2. Ентропія Шеннона для ансамблю автогенераторів

Для прикладу подивимося, як вводиться поняття ентропії для ансамблю автогенераторів Ван-дер-Поля (вони ж – автогенератори томсонівського типу, або -генератори).

Для зручності подальших розрахунків запишемо рівняння для такого автогенератора у формі симетризованої системи двох рівнянь першого порядку:

(1.1.31)

де використано позначення: – узагальнена координата (це може бути, наприклад, заряд на конденсаторі в контурі автогенератора), – узагальнена швидкість, – енергія коливань, – параметр лінійного тертя (додатні відповідають від’ємній дисипації), – параметр нелінійного тертя.

Якщо та можна вважати малими порівняно з (це характерно для квазігармонічного режиму коливань), то систему (1.1.31) можна звести до рівняння

(1.1.32)

– узагальненого рівняння Релея¹¹ – Ван-дер-Поля.

З іншого боку, система (1.1.31) зводиться до одного рівняння для енергії

, (1.1.33)

яке має стійкий стаціонарний розв’язок , що відповідає усталеним коливанням.

Як відомо з курсу статистичної радіофізики¹², реальний автогенератор томсонівського типу описується неоднорідним рівнянням Релея (або Ван-дер-Поля), в правій частині якого стоїть випадкова сила, обумовлена внутрішніми шумами. Цю силу визначають, головним чином, теплові та дробові шуми. В результаті дії вказаної сили поведінка автогенератора набуває випадкового характеру.

Нагадаємо також, що ширина лінії автогенератора визначається двома процесами – флуктуаціями амплітуди, які можна характеризувати шириною спектру, та флуктуаціями фази, які можна вважати дифузійним випадковим процесом і характеризувати коефіцієнтом дифузії фази.

З урахуванням згаданих процесів рівняння (1.1.33) для енергії коливань набуває вигляду

, (1.1.34)

де – інтенсивність шуму, що в загальному випадку залежить від інтенсивності коливань, – випадкова зовнішня сила, що задовольняє умовам , . Другий доданок у правій частині (1.1.34) враховує, що наявність шумів приводить до додаткового зменшення інтенсивності сигналу¹³.

Отже, з урахуванням дії випадкових шумів можна розглянути статистичний ансамбль (ансамбль Гіббса – див. п.1.1.3.1) автогенераторів і охарактеризувати його деякою функцією розподілу – наприклад, функцією розподілу по енергіях .

За відомим стохастичним диференціальним рівнянням можна записати так зване рівняння Фоккера¹⁴ - Планка¹⁵ для густини розподілу ймовірності (функції розподілу).

Нехай стохастичне диференціальне рівняння для випадкової величини х має вигляд

, (1.1.35)

де та – довільні функції випадкової змінної , а випадкова функція часу має нульове середнє і є -корельованою, тобто задовольняє умовам

, , (1.1.36)

де – дисперсія випадкового процесу . Тоді рівняння Фоккера - Планка для густини розподілу ймовірності має вигляд:

, (1.1.37)

де використані позначення

, . (1.1.38)

Стаціонарний розв’язок рівняння Фоккера - Планка (який досягається при ) можна записати у вигляді:

, (1.1.39)

де константу можна знайти з умови нормування.

Знаючи стохастичне диференціальне рівняння (в нашому випадку – рівняння (1.1.34) з випадковою зовнішньою силою), можна записати рівняння Фоккера - Планка для функції розподілу. Зокрема, для функції розподілу за енергією у припущенні, що шуми характеризуються сталою інтенсивністю , воно має вигляд:

. (1.1.40)

Стаціонарний розв’язок рівняння (1.1.40) може бути поданий у формі канонічного розподілу Гіббса:

, (1.1.41)

де – вільна енергія, яку можна знайти з умови нормування (1.1.22):

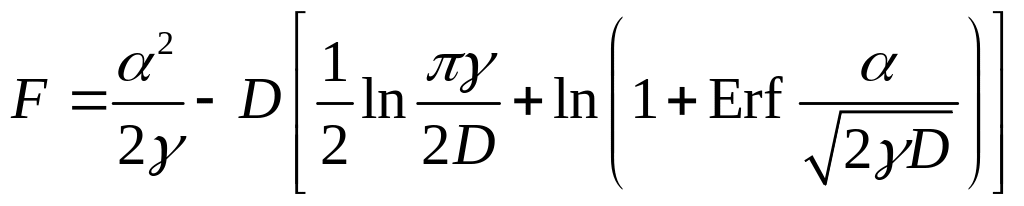. (1.1.42)

Тут використано позначення

– інтеграл ймовірностей (функція похибок).

Знаючи розподіл , можна розрахувати ентропію Шеннона за формулою (1.1.30):

. (1.1.43)

Зокрема, для найпростішого випадку (зворотний зв’язок відсутній) та (нелінійність відсутня), коли , поклавши , отримаємо .