
- •1. Свойства жидкостей и газов
- •2. Основные положения теории напряженного состояния жидкостей
- •3. Давление жидкости
- •4. Уравнение равновесия жидкости
- •5. Равновесие однородной несжимаемой жидкости в поле сил тяжести. Закон паскаля. Гидростатический закон распределения давления
- •6. Определение силы давления жидкости на поверхности тел
- •Плоская поверхность
- •7. Уравнение неразрывности. Понятие линии и трубки тока
- •8. Уравнения движения идеальной жидкости (уравнения эйлера)
- •9. Уравнение бернулли
- •Энергетический смысл уравнения Бернулли
- •Уравнение Бернулли в геометрической форме
5. Равновесие однородной несжимаемой жидкости в поле сил тяжести. Закон паскаля. Гидростатический закон распределения давления
Проинтегрируем
основное уравнение гидростатики в
предположении, что
![]() (жидкость несжимаема), а из массовых сил
действует только сила тяжести. В этом
случае
(жидкость несжимаема), а из массовых сил
действует только сила тяжести. В этом
случае
![]() ,
,
![]() ,
т. е.
,
т. е.
![]() ,
и после интегрирования
,
и после интегрирования
![]()
 ,
,
где C – произвольная постоянная. Для ее нахождения используем следующее граничное условие:
при
![]()
![]() .
.
После подстановки в уравнение получим
![]() ,
,
![]() .
.
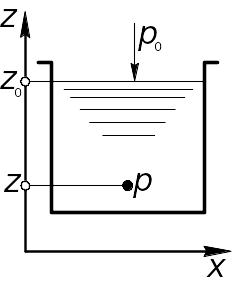
Как видно из рисунка,
разность (![]() )
– глубина погружения рассматриваемой
частицы, которую будем обозначать
буквой h, т. е.
)
– глубина погружения рассматриваемой
частицы, которую будем обозначать
буквой h, т. е.
![]() .
.
Полученное уравнение выражает известный из курса физики закон Паскаля: давление, действующее на поверхность, передается по всем направлениям одинаково.
Очевидно,
что член
![]() должен выражаться в единицах давления,
т. е. в паскалях (1 Па = 1 Н/м2).
Эту величину называют избыточным
давлением.
Она может быть как положительной, так
и отрицательной. Такая трактовка приводит
нас к понятию абсолютного
давления,
которое в соответствии с приведенным
выше уравнением может быть представлено
как сумма барометрического (атмосферного)
и избыточного давления, т. е.
должен выражаться в единицах давления,
т. е. в паскалях (1 Па = 1 Н/м2).
Эту величину называют избыточным
давлением.
Она может быть как положительной, так
и отрицательной. Такая трактовка приводит
нас к понятию абсолютного
давления,
которое в соответствии с приведенным
выше уравнением может быть представлено
как сумма барометрического (атмосферного)
и избыточного давления, т. е.
![]() .
.
Отрицательное избыточное давление называют вакуумом.
Вернемся
вновь к уравнению для гидростатического
давления. После деления обеих его частей
на
![]() получаем
получаем
![]() .
.
В таком виде все его члены выражаются
в единицах длины и носят название
напоров. Величина z характеризует
положение жидкой частицы над произвольно
выбираемой горизонтальной плоскостью
отсчета, т. е. z – это
геометрический напор;
![]() – пьезометрический напор. Сумму
этих величин
– пьезометрический напор. Сумму
этих величин ![]() называют гидростатическим напором.
Чтобы уяснить физический смысл этих
величин, рассмотрим простую схему,
показанную на рисунке.
называют гидростатическим напором.
Чтобы уяснить физический смысл этих
величин, рассмотрим простую схему,
показанную на рисунке.
П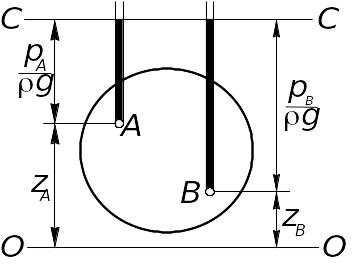 редставим
герметично закрытый сосуд, заполненный
жидкостью, находящейся под давлением.
Выберем в этом со-суде две произвольно
расположенные точки A и B и,
опять-та-ки произвольно, горизонтальную
плоскость O–O,
которую назовем плоскостью отсчета.
редставим
герметично закрытый сосуд, заполненный
жидкостью, находящейся под давлением.
Выберем в этом со-суде две произвольно
расположенные точки A и B и,
опять-та-ки произвольно, горизонтальную
плоскость O–O,
которую назовем плоскостью отсчета.
Координаты
частиц, расположенных в точках
A
и
B,
будут ![]() и
и
![]() .
В соответствии со сказанным выше величины
и
выражают
геометрический напор. Теперь через
крышку со-суда введем в точках A
и B
сообщенные с атмосферой стеклянные
трубки. Эти трубки называют пьезометрами.
Поскольку по условию жидкость находится
под давлением, то она начнет подниматься
по пьезометрам. Не представляет труда
и ответ на вопрос о том, когда прекратится
подъем. Очевидно, что это произойдет в
тот момент, когда высота столба жидкости
уравновесит давление в рассматриваемой
точке. Это и есть пьезометрическая
высота
либо пьезометрический напор.
.
В соответствии со сказанным выше величины
и
выражают
геометрический напор. Теперь через
крышку со-суда введем в точках A
и B
сообщенные с атмосферой стеклянные
трубки. Эти трубки называют пьезометрами.
Поскольку по условию жидкость находится
под давлением, то она начнет подниматься
по пьезометрам. Не представляет труда
и ответ на вопрос о том, когда прекратится
подъем. Очевидно, что это произойдет в
тот момент, когда высота столба жидкости
уравновесит давление в рассматриваемой
точке. Это и есть пьезометрическая
высота
либо пьезометрический напор.
Вышеуказанное
соотношение справедливо для любых
произвольно выбранных частиц покоящейся
жидкости, поэтому в общем виде его можно
записать как
![]() ,
т. е. для любых точек жидкости
гидростатический напор одинаков.
Следовательно, уровни в пьезометрах
установятся на одной и той же высоте
(плоскость C–C
на
рисунке). Это уравнение выражает так
называемый гидростатический
закон распределения давления.
,
т. е. для любых точек жидкости
гидростатический напор одинаков.
Следовательно, уровни в пьезометрах
установятся на одной и той же высоте
(плоскость C–C
на
рисунке). Это уравнение выражает так
называемый гидростатический
закон распределения давления.
