1.5. Визначений інтеграл

Обчислення визначеного інтеграла
Назва	Аналітичний запис
Формула Ньютона-Лейбніца	, де – F(x) первісна функції f(x) на [a;b], - знак подвійної підстановки
Формула заміни змінної у визначеному інтегралі
Формула визначеного інтегрування частинами

Застосування визначеного інтеграла (геометричні задачі)
Назва поняття	Геометричне зображення	Формули для обчислення
1	2	3
Площа плоскої фігури: а) площа криволінійної трапеції, якщо		а) криву задано явно: б) криву задано параметрично:
б) площа криволінійної трапеції, якщо
в) площа фігури, зображеної на рисунку
г) площа фігури, обмеженої кривими y=f1(x), y=f2(x) та прямими x=a, x=b

1	2	3
Довжина дуги кривої		а) криву задано явно: б) криву задано параметрично:
Об’єм тіла обертання

Запитання для самоконтролю

1. Дайте означення визначеного інтеграла. Які його властивості?

2. Запишіть формулу Ньютона-Лейбніца.

3. Які основні методи обчислення визначених інтегралів Ви знаєте?

4. Дайте означення невласних інтегралів І-го і ІІ-го роду. Як вони обчислюються?

5. Наведіть приклади задач з геометрії і фізики, що розв’язуються за допомогою визначеного інтеграла. Запишіть необхідні формули.

Рекомендована література: [1], розділ 4, п.4.2; [8], розділ XI, §1-7, розділ XII, §1-7; [5], ч.3, практичні заняття 10-13, 15-16.

Приклад 5.1. Знайти інтеграли:

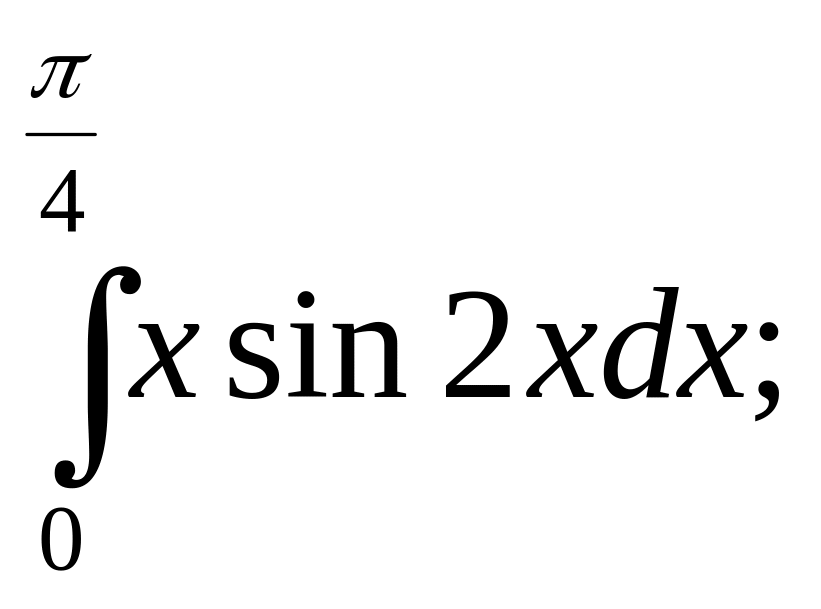а) б) в)

Розв’язання. а) Використаємо метод підведення під знак диференціала.

б) Застосуємо формулу визначеного інтегрування частинами:

Тоді

в) Обчислимо інтеграл, використавши метод заміни змінної.

Приклад 5.2. Обчислити невласні інтеграли або довести їх розбіжність:

а) б)

Розв’язання. а) Маємо невласний інтеграл першого роду.

Інтеграл збігається.

б) Маємо невласний інтеграл другого роду.

Підінтегральна функція терпить нескінчений розрив при х = 0.

Інтеграл розбігається.

П риклад 5.3. Обчислити площу фігури, обмеженої лініями

у = 3х – х², у = -х.

Р озв’язання. Знайдемо точки перетину прямої у =f₁(x)= -х і параболи у = f₂(x)= 3х- .

Точки перетину ліній О(0;0) і А(4;-4).

Площа цієї фігури:

Завдання для самоконтролю

1. Знайти інтеграли:

а) ; б) ; в) .

2. Обчислити невласні інтеграли або довести їх розбіжність:

а) ; б) .

3. Обчислити площу фігури, обмеженої лініями:

а) ; б) .