
- •Передмова
- •1.2. Вступ до математичного аналізу
- •Запитання для самоконтролю
- •Завдання для самоконтролю
- •1.3. Похідна та її застосування
- •Правила диференціювання
- •Запитання для самоконтролю
- •Завдання для самоконтролю
- •1.4. Невизначений інтеграл
- •Запитання для самоконтролю
- •Завдання для самоконтролю
- •1.5. Визначений інтеграл
- •Запитання для самоконтролю
- •Завдання для самоконтролю
- •1.6. Звичайні диференціальні рівняння
- •Запитання для самоконтролю
- •Завдання для самоконтролю
1.2. Вступ до математичного аналізу
Основні теореми про границі |
|
Якщо
існують
|
Аналітичний запис |
Границя алгебраїчної суми двох (скінченної кількості) функцій дорівнює алгебраїчній сумі границь цих функцій. |
|
Границя добутку двох (скінченної кількості) функцій дорівнює добутку границь цих функцій. |
|
Границя частки двох (скінченної кількості) функцій дорівнює частці границь цих функцій за умови, що границя дільника не дорівнює нулеві |
|
Сталий множник можна виносити за знак границі. |
|
Границя цілого додатного степеня функції дорівнює тому ж степеню границі функції. |
|
Визначні границі та їх наслідки |
|
Назва |
Аналітичний запис |
1 |
2 |
Перша визначна границя |
|
1 |
2 |
Наслідки |
1.
2.
3.
4.
5.
|
Друга визначна границя |
|
Наслідки |
1. 2.
|
Неперервність функції в точці |
|
Назва поняття |
Означення |
х0 – точка неперервності функції f(x)
|
2.
Існує
|
1 |
2 |
|
3.
Виконується
рівність
|
х0 – точка розриву функції f(x) |
Не виконується одна з умов 1-3. |
Класифікація точок розриву функції |
|
Назва |
Означення |
х0 – точка розриву першого роду: а) усувний розрив
|
|
б) неусувний розрив ( |
|
х |
Хоча б одна з
границь
|
Запитання для самоконтролю
Що називають функцією однієї змінної? Її областю визначення? Множиною значень?
Назвіть основні елементарні функції. Згадайте їх властивості і графіки.
Дайте означення границі послідовності, функції.
Сформулюйте основні властивості границь.
Запишіть і виведіть І-шу і ІІ-гу визначні границі.
Які границі називаються односторонніми?
7. Сформулюйте означення неперервної функції в точці і на інтервалі.
Що таке точки розриву функції? Як вони класифікуються?
Рекомендована література: [1], розділ 2;[8],розділ I,II; [5], ч.2, практичні заняття 1-20.
Приклад 2.1. Знайти область визначення функцій:
а)
![]() б)
б)
![]()
Розв’язання. а) При знаходженні області визначення даної функції потрібно згадати, що корінь парного степеня може існувати лише для невід’ємних чисел, а знаменник дробу повинен бути відмінним від нуля. Ці умови повинні виконуватись одночасно. А тому шукана область визначення являє собою розв’язок системи:
![]()
Зобразимо її на рисунку.

Рис.3
Відповідь:
![]() .
.
б) З того, що логарифм існує для строго додатних чисел, а вираз, який міститься під знаком функції arcsin, за модулем не перевищує одиниці, маємо систему:
![]()
Зобразимо область визначення даної функції на рисунку.

Рис.4
Відповідь:
![]() .
.
Приклад 2.2. Знайти границі функцій:
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]() д)
д)
![]()
Розв’язання.
а) При
![]() маємо неозначеність виду
маємо неозначеність виду
![]() Щоб її розкрити, поділимо почленно
чисельник і знаменник дробу на х
у
найвищому степені (в нашому випадку на
х2).
Маємо
Щоб її розкрити, поділимо почленно
чисельник і знаменник дробу на х
у
найвищому степені (в нашому випадку на
х2).
Маємо


Зауважимо,
що при
величини
![]() та
та
![]() – нескінченно малі, а тому
– нескінченно малі, а тому
![]()
б)
Безпосередня підстановка граничного
значення х=-2
дає неозначеність виду
![]() Щоб
розкрити цю неозначеність, виділимо в
чисельнику і знаменнику дробу множник
х+2
і скоротимо на нього. (Множник х+2
обов’язково увійде в розклад на множники
многочленів в чисельнику і знаменнику
дробу, оскільки х=-2
– корінь обох многочленів. Зауважимо,
що скорочення можливе, бо х+2≠0,
хоча
й
(х+2)→0).
Щоб
розкрити цю неозначеність, виділимо в
чисельнику і знаменнику дробу множник
х+2
і скоротимо на нього. (Множник х+2
обов’язково увійде в розклад на множники
многочленів в чисельнику і знаменнику
дробу, оскільки х=-2
– корінь обох многочленів. Зауважимо,
що скорочення можливе, бо х+2≠0,
хоча
й
(х+2)→0).
![]()
Для виділення множника х+2 в чисельнику і знаменнику дробу
виконаємо ділення квадратних тричленів на двочлен:


в)
Безпосередня підстановка граничного
значення х=6
дає неозначеність виду
Щоб її розкрити, звільнимося від
ірраціональності у знаменнику. Для
цього домножимо чисельник і знаменник
дробу на вираз, спряжений до знаменника,
тобто, на
![]()
![]()
![]()
![]()
г) Для
знаходження даної границі використаємо
наслідок з першої визначної границі
![]() У нашому випадку
У нашому випадку
![]() =
=![]()
д) При
![]() маємо неозначеність виду
маємо неозначеність виду
![]() .
Щоб її розкрити скористаємося наслідком
з другої визначної границі
.
Щоб її розкрити скористаємося наслідком
з другої визначної границі
![]()
Для цього поділимо чисельник і знаменник основи степеня на 2х. Маємо:
 Приклад
2.3.
Дослідити функцію на неперервність і
побудувати її графік:
Приклад
2.3.
Дослідити функцію на неперервність і
побудувати її графік:
![]()
Розв’язання.
Ф ункція
визначена для всіх
ункція
визначена для всіх
![]() .
Розрив можливий лише в точці х=2,
при переході через яку функція змінює
свій аналітичний вираз.
.
Розрив можливий лише в точці х=2,
при переході через яку функція змінює
свій аналітичний вираз.
Знаходимо односторонні границі:

В точці х=2 функція має скінченний розрив (розрив першого роду).
“Стрибок”
функції:
![]()

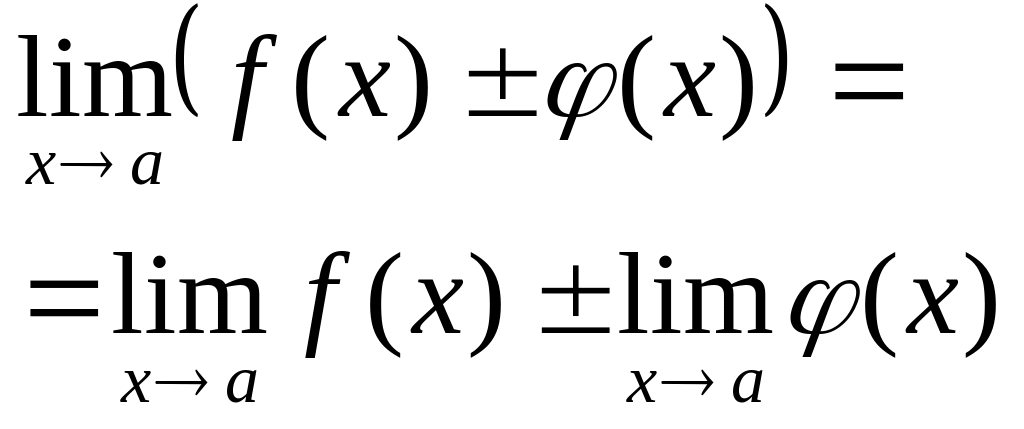





 розрив
типу „стрибка”)
розрив
типу „стрибка”) 0
– точка розриву другого роду
0
– точка розриву другого роду