3.21 Принятие решений по стратегии последующего эксперимента:
Диаграмма рангов может иметь следующий вид:
1. Распределение (различие в рангах) факторов и их убывание равномерное. В этом случае уровень априорной информации весьма низок, и поэтому все факторы должны включаться в эксперимент.
2. Распределение равномерное, а убывание неравномерное. В этом случае, если возможно, лучше включить в физический эксперимент все факторы, но возможен и априорный отсев их.
3. Распределение неравномерное, а убывание равномерное. Возможен априорный отсев факторов с низким рангом.
4. Распределение и убывание неравномерное (например, экспоненциальное). Это наиболее благоприятная ситуация, так как нужно отсеить ряд факторов, отнесенных к шумовому полю.
Пример:
Ранговая диаграмма факторов, рассмотренная в примере, относится к типу 2 (см. рис. 1). В результате анализа этой диаграммы для дальнейших исследований было отобрано 7 факторов, занимающих 7 первых мест.
3.22 Сравнение мнений двух групп экспертов.
В
том случае, когда есть необходимость
статистического сравнения мнений двух
групп экспертов (различные специальности,
представители различных школ и т.д.),
можно воспользоваться коэффициентом
ранговой корреляции Спирмена (таблица
П2). Если
, то между мнениями 2-х групп экспертов
имеется связь с достоверностью 95%.
Предположим,
что пример, приведенный в первой части
настоящей методики (подпункты от 1 до
20), рассчитывался на основании априорной
информации, полученной от группы
экспертов-конструкторов. Аналогично
проводилась обработка априорной
информации, в данном случае чисто
условной, полученной от второй группы
экспертов-технологов W = 0,7989 и.
При этом проводим статистическое
сравнение мнений двух групп экспертов.
3.22.1 Заполняем исходные графы табл. 3. Во вторую и третью строки заносятся суммы рангов первой и второй групп экспертов. Затем этим суммам присваиваются ранги от 1 до n (строки 3 и 4).
3.22.2 Вычисляем отклонение рангов:
.
(13)
Пример: см. строку 5 табл. 3.
3.22.3 Вычисляем квадраты отклонений рангов:
.
(14)
Пример: см. строку 6 табл. 3.
3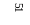
.22.4
Вычисляем сумму
квадратов отклонений рангов.
.
(15)
Пример:
Sp = 16 + 1 + 6,25 + 0,25 = 23,5.
3.22.5 Определяем коэффициент ранговой корреляции по Спирмену:
а) для несвязанных рангов
; (16)
б) для связанных рангов
;
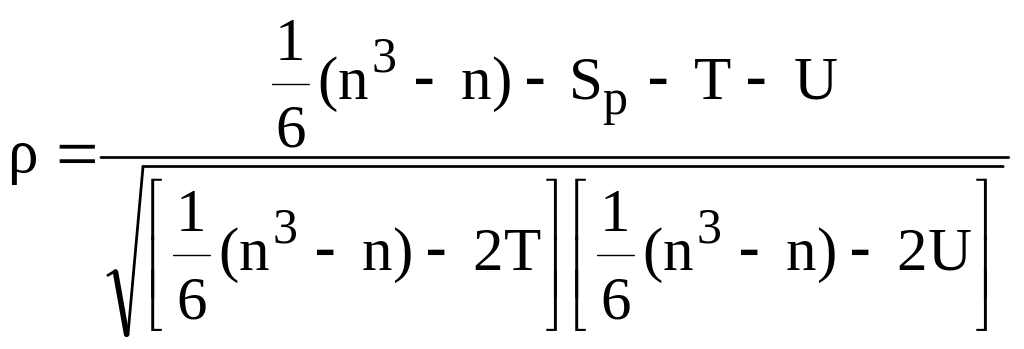(17)
; 
,
где t и U – количество повторений рангов в 3-й и 4-й строках табл. 3.
Пример:
Т = 0, так как в 3-й строке табл. 3 нет связанных рангов.
U = 1/12×(8 – 2) = 0,5.
.
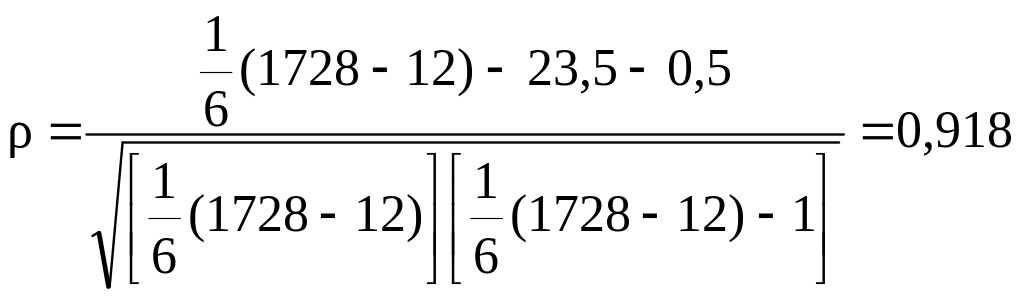Значения
коэффициента
в зависимости от согласованности
ранжирования могут меняться от 1
(ранжированные ряды совпадают) до –1
(корреляция отсутствует).
3.22.6 Определение значимости коэффициента .
При количестве ранжируемых объектов более 10 распределение стремится к нормальному со стандартом отклонений:
;
. (18)
Пример:
;
.
Согласованность ранжировок определяем по таблице П2 приложения. Для Z = 3,04 получаем значимость p = 0,99.