1.3. Особенности формирования уравнений состояния
в индуктивно связанных цепях
В электрических цепях связь контуров может осуществляться не только через R, L, C – двухполюсники, но и посредством индуктивно связанных элементов (ИСЭ).
ИСЭ (рис.3)
состоит из двух индуктивностей L1
и L2, которые связаны общим
магнитным потоком и не имеют внутренней
электрической связи. Магнитная связь
характеризуется коэффициентом взаимной
индукции М, полнота связи –
коэффициентом магнитной связи
.
Вебер-амперные характеристики ИСЭ имеют вид
;
,
– вектора потокосцеплений и токов; L
– матрица индуктивностей,
;
.
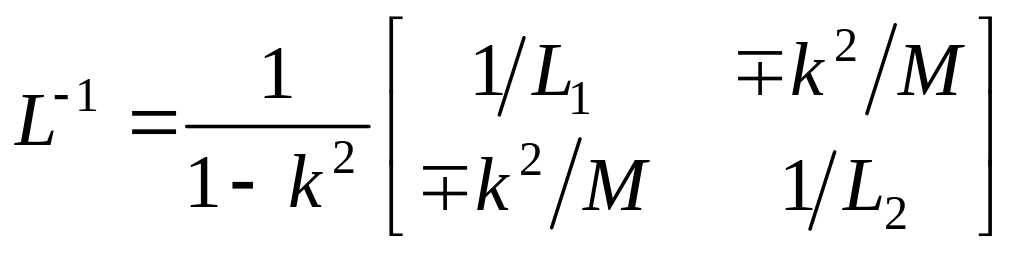Верхний знак соответствует согласному, нижний – встречному включению элементов L1 и L2.
Напряжения
и токи i = [i1, i2]T
связаны дуальными соотношениями:
(16)
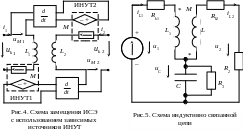
Напряжения uk1 и uk2 уравновешивают соответствующие ЭДС само- и взаимоиндукции uk = uL uM. Напряжение взаимной индукции uM можно учесть с помощью источника напряжения, управляемого током (ИНУТ): uM1,2 = МDi2,1, где D = d/dt – оператор дифференцирования. Тогда в соответствии с формулой (16) ИСЭ можно представить схемой замещения, состоящей из L-элементов и зависимых источников напряжения. Реализация такой модели ИСЭ в среде Electronics Workbench показана на рис.4.
ИСЭ может быть включен во внешнюю цепь по последовательной, параллельной, трансформаторной и автотрансформаторной схемам. Рассмотрим схему с резистивно-емкостной и автотрансформаторной связью (рис.5).
Для получения
уравнений относительно переменных
состояния x = [iL1, iL2, uC]T
в стандартной форме Коши (1) воспользуемся
уравнениями (16) в виде
Напряжения
и ток
выразим через токи
и напряжения
и
с помощью уравнений Кирхгофа:
.
Объединение уравнений ИСЭ и уравнений Кирхгофа дает требуемую форму уравнений состояния (1), для которых матрицы А и В имеют вид
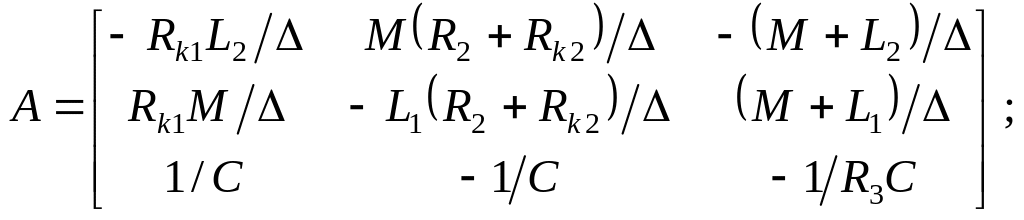
Уравнения относительно потокосцеплений получают аналогичным образом.
2. Подобие электрических цепей
2.1. Нормирование параметров
Если в цепи заданной структуры определенным образом изменить параметры элементов и параметры сигнала, не изменяя его формы, то можно добиться того, что реакции в исходной и преобразованной цепях будут подобны. Это позволяет моделировать процессы в ускоренном, реальном и замедленном времени, представлять временные и частотные характеристики цепи в обобщенном виде.
Рассмотрим две
цепи NW и NW',
сигнальные графы и структуры
ветвей которых совпадают, а параметры
отличаются. В качестве исходной
цепи NW рассмотрим передающую цепь (см.
рис.1), имеющую
следующие параметры: R1 = R2 = 50 Ом,
R3 = 10 Ом, С = 10 мкФ,
L = 67 мГн.
Входной сигнал задан, например,
экспоненциальным импульсом
с параметрами Um =
= 10 В, τi = 1 мс.
Параметры цепи NW' определяются через константы подобия
(17)
Напряжение и ток элементов цепи связаны компонентными уравнениями – законом Ома для R-элемента и дифференциальными соотношениями (3) для L- и С-элементов. Тогда между константами подобия также существует связь
.
(18)
Поэтому из семи констант (17) независимыми являются три. Зададимся константами Nt = 0,1, NR = 5, Nu = 1. После вычисления других констант по формулам (18) NC = 0,02, Nω = 10, Ni = 0,2, NL = 0,5 получим искомые параметры подобной цепи: R1' = = R2' = 250 Ом, R3' = 50 Ом, С' = 0,2 мкФ, L' = 33,5 мГн, Um' = 10 В, τi' = 100 мкс.
Подобие реакций в цепях NW и NW' обусловлено одинаковой кратностью изменения параметров сигнала и параметров собственных колебаний, зависящих от первичных параметров.
При исследовании
процессов удобно пользоваться
нормированными величинами
,
где
– базовое значение. Выбор базовых
значений производится аналогично выбору
констант подобия: три величины выбираются
произвольно, остальные вычисляются по
формулам
.
(19)
Запишем уравнения
состояния (12), (13) исходной цепи (см. рис.1)
с указанными параметрами в безразмерном
виде. В качестве базовых величин примем
параметры импульса tб = τi = 1 мс,
Uб = Um = 10 В
и сопротивление Rб = 100 Ом.
Вычисление по формулам (19) других базовых
величин Lб = 100 мГн,
Сб = 10 мкФ дает
значение безразмерных параметров цепи:
,
,
,
.
Входной сигнал имеет форму
.
Для безразмерных параметров цепи матрицы A, B, С, D уравнений состояния (12), (13) принимают значения
;
;
;
.
(20)
В дальнейшем анализ цепей будем производить в безразмерном виде, опуская знак нормировки.