6.2. Определение реакций на импульсные сигналы

В соответствии с формулой Дюамеля (62) выходная реакция четырехполюсника на прямоугольный импульс с параметрами U_m, t_и (см. рис.10) записывается для двух временных интервалов

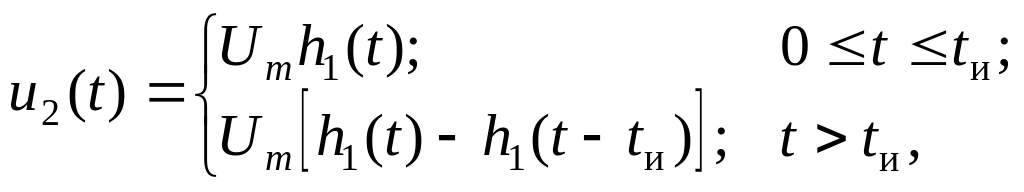
где h₁(t) – переходная характеристика, определяемая формулой (46).

Сигнал u₁(t) можно представить в виде наложения смещенных во времени ступенчатых функций . Тогда реакция находится как сумма переходных характеристик, одна из которых задержана на время t_и

.

Форма выходного сигнала u₂(t) зависит от соотношения между параметрами переходной характеристики ₁, ₂ и длительностью импульса t_и. Из графика u₂(t) (рис.26) следует, что в интервале реакция совпадает с переходной характеристикой цепи. В области вынужденные реакции компенсируют друг друга и выходной сигнал определяется наложением только свободных составляющих.

Если длительность сигнала превышает время установления , то реакции цепи на фронт и срез импульса становятся независимыми. При дальнейшем увеличении длительности импульса выходное напряжение по форме приближается к реакции дифференцирующего звена. При уменьшении длительности сигнала реакция в интервале изменяется по линейному закону, как это имеет место при прохождении импульса через интегрирующую цепь.

Для экспериментального определения переходной характеристики можно использовать периодическую последовательность прямоугольных импульсов, следующих с периодом Т. Длительность импульса должна превышать длительность переходного процесса . Период Т выбирается из условия, что к моменту поступления очередного импульса реакция на предыдущий импульс должна успеть затухнуть.

Рассмотрим реакцию четырехполюсника на импульс кусочно-линейной формы (см. рис.10)

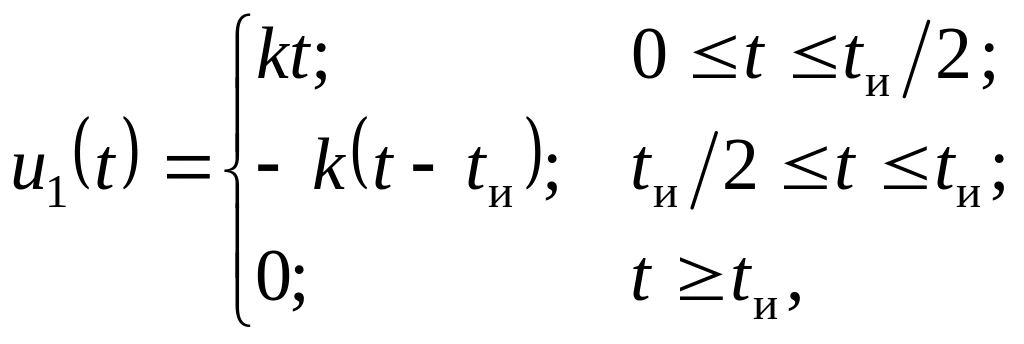
где ; U_m – амплитуда; t_и – длительность импульса.

Реакция находится по формуле (62), в которой в зависимости от интервала наблюдения:

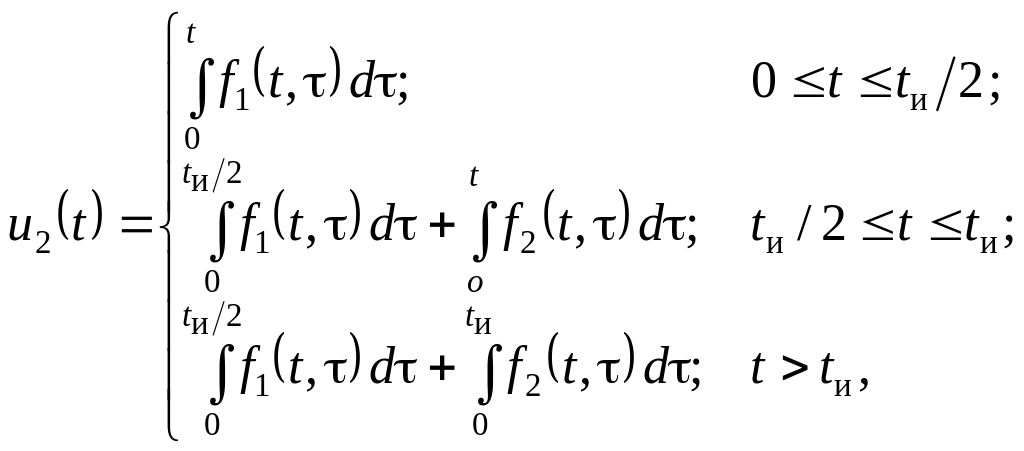(63)

где .

Реакция на первом интервале с точностью до множителя k совпадает с реакцией цепи на функцию единичного наклона . Первое слагаемое реакции на интервале учитывает состояние цепи в момент , обусловленное переходным процессом на первом интервале. При реакция определяется запасом энергии в цепи после прекращения действия импульса.

Реакцию цепи можно получить в более простом и наглядном виде, если записать входной сигнал в виде наложения смещенных во времени линейных напряжений

.

Тогда в соответствии с принципом суперпозиции выходной сигнал можно представить как сумму задержанных реакций на функцию единичного наклона:

. (64)

Первое слагаемое этого выражения совпадает с реакцией цепи на первом интервале в формуле (63).

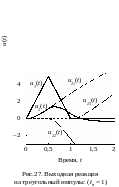
На рис.27 показаны графики выходного сигнала и его составляющих , , . Расчет выполнен по формуле (64), в которой h₂(t) определяется выражением (56). Из графиков видно, что прохождение сигнала ( , , ) через передающую цепь сопровождается искажением его формы и задержкой во времени. При увеличении длительности импульса проявляются дифференцирующие свойства четырехполюсника.

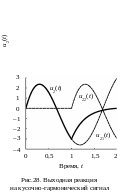
Найдем реакцию на кусочно-непрерывный сигнал в виде косинусоидального импульса, в котором имеются две точки разрыва

где ; – период колебаний частотой .

Поскольку в моменты t₁ = 0 и t₂ = T/2 имеет место ступенчатое изменение сигнала, то интеграл Дюамеля запишем в виде

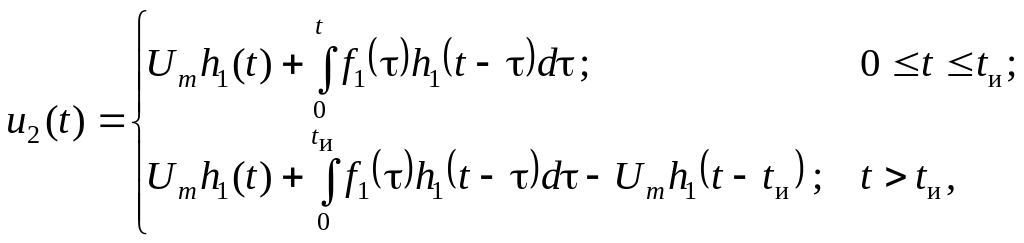
г де .

Если представить входное напряжение в виде наложения задержанных сигналов, то приходим к другой форме записи реакции. Заданный сигнал можно рассматривать как сумму двух гармонических колебаний и , смещенных во времени на , .

Для нахождения общей реакции достаточно найти частную реакцию на первую составляющую входного сигнала и затем записать полную реакцию в соответствии с принципом суперпозиции

; .

Реакцию найдем с помощью интеграла Дюамеля

,

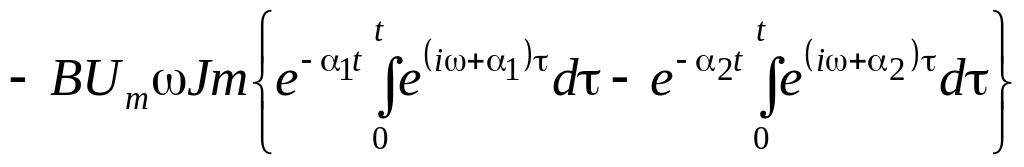где ; ; – параметры переходной характеристики , определяемые по формуле (46).

Интегрирование приводит к выражению

,

где ; ; ; .

Установившаяся и свободная составляющие реакции u₂₁(t) совпадают с соответствующими слагаемыми формулы (59), полученной классическим методом.

Из графика выходного сигнала (рис.28) следует, что в области вынужденные составляющие компенсируют друг друга и реакция определяется в основном свободной составляющей с постоянной времени .

Приведенные примеры показывают, что представление интеграла наложения в виде суммы задержанных реакций на ступенчатые, линейные и гармонические сигналы, с помощью которых синтезируется исходный сигнал, позволяет упростить расчет и более наглядно отразить влияние на форму выходного сигнала соотношения между длительностью импульса и параметрами свободных процессов, к которым относятся постоянные времени цепи и период собственных колебаний. Метод интеграла Дюамеля наиболее удобен при вычислении реакций на сигналы, которые можно представить с помощью кусочно-ступенчатых и кусочно-линейных функций.

Если известна реакция на импульс , то реакцию на периодическую последовательность импульсов также можно найти методом наложения:

,

где Т – период следования импульсов.