Работа с матрицами Вычисление определителя матрицы

Процесс вычисления определителя матрицы (массива) даже выше третьего порядка трудоемок, но возможности MS Excel позволяют быстро и верно найти его. Например, чтобы вычислить определитель матрицы 4-го порядка, нужно:

1. ввести в ячейки листа MS Excel значения элементов матрицы по строкам, активизировать любую пустую ячейку, например С8, в которой будет получен результат вычисления определителя;

2. вызвать f_x (Функция…) меню Вставка (для MS Excel 2010 это меню Формула);

3. найти функцию МОПРЕД категории Математические (рис. 20);

Рис. 20

4. откроется вспомогательное окно Аргументы функции (рис. 21);

Рис. 21

5. В поле Массив помещаем адрес диапазона, в котором размещены элементы матрицы, например, B3:E6.

6. В указанной ранее ячейке, например С8, получим результат (рис. 22).

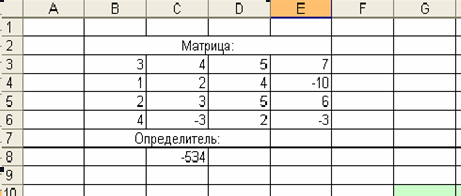
Рис. 22

Умножение матриц

При умножении двух матриц должна получиться матрица. Математический процесс нахождения произведения матриц трудоемок, сводится к вычислению сумм произведений по формуле. В MS Excel достаточно задать элементы матриц на листе по строкам, затем обратиться к функции МУМНОЖ Математической категории (рис. 23).

Получаем первый элемент произведения матриц. Он равен 6. Для получения всех элементов матрицу, выделяем место под матрицу-произведение нужной размерности, начиная с первого элемента, нажимаем клавишу F2 клавиатуры (рис. 24), затем Shft+Ctrl+Enter

Рис. 23

Рис. 24

Рис. 25

Вычисление обратной матрицы

Вычисление обратной матрицы осуществляется при помощи функция МОБР, принадлежащей категории Математические. Процесс вычисления обратной матрицы аналогичен вычислению произведения матриц.

Примечание. Обратной для А называется матрица В, если ее произведение с исходной А×В=Е, Е единичная матрица. Нахождение обратной матрицы – это, по существу, решение системы линейных уравнений.

Размещаем на листе матрицу (рис. 26) и обращаемся к соответствующей функции.

Активируем на листе ячейку, которая для матрицы обратной будет первым элементом, нажимаем F2, что покажет формулу, затем выделяем диапазон для результата, нажимаем Shft+Ctrl+Enter и получаем обратную матрицу (рис. 27). Правильность можно проверить с помощью произведения прямой и обратной. Получится единичная матрица.

Рис. 26

Рис. 27

Нахождение транспонированной матрицы

Категория функций Ссылки и массивы дает возможность получить транспонированные массивы, а именно такие, у которых индексы строк и столбцов меняются местами А_ij=T_ji (пример на рис. 28).

Рис. 28

Транспонируем матрицу Аij, в данном случае A1:D4 (рис. 29), вызвав, функцию ТРАНСП категории Ссылки и массивы (рис. 30).

Рис. 29

Для транспонированной матрицы нужен диапазон (это второй массив).

Рис. 30

Заполняем поле Массив (рис. 31).

Рис. 31

Получаем первый элемент транспонированной матрицы, выделяем место под всю матрицу, начиная с первого полученного элемента. Нажимаем клавишу F2, затем Shft+Ctrl+Enter. Строки поменялись местами со столбцами (рис. 32).

Рис. 32

Решение систем линейных уравнений

Применим функции МОБР, МУМНОЖ, МОПРЕД для решения систем линейных уравнений с несколькими неизвестными с помощью матричных функций в Excel (рис.33).

Рис. 33

Вектор неизвестных С11:С12 был получен с помощью функции МУМНОЖ обратной матрицы D7:E8 на столбец A11:A12.