Інформаційні системи та технології.

Зміївська І.В., Обоянська Л.А.

Практичне занятtя тема занятия: транспортные задачи. Задача о назначениях. Линейное программирование.

Тема занятия. Линейное программирование. Транспортные задачи.

Цель занятия: Изучить методы и алгоритмы решения транспортных задач с использованием технологий MS EXCEL

Постановка транспортной задачи.

Транспортная задача. Имеются n пунктов производства, в которых сосредоточен некоторый однородный груз в количестве а_1,а_{2 …,} а_n единиц. Указанный груз необходимо доставить в m пунктов назначения. Заявки на доставку груза составляют b_1, b2, …, b_m единиц. Стоимость перевозки единицы продукции с i-го пункта производства в j-й центр распределения с_ij приведена в таблице, где под строкой понимается пункт производства, а под столбцом - пункт распределения. Кроме того, в этой таблице в i-й строке указан объем производства в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения.

Предполагается что количество груза, находящегося в пунктах отправления, равно суммарному количеству, которое необходимо доставить потребителям закрытая модель ТЗ.

Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.

Математическая формулировка задачи.

Обозначим x_ij – количество груза доставляемое из i - того пункта отправления в j-тый пункт назначения. Необходимо найти вектор X=(x_{11, X12, … , X1m, X21, X22, … X2m, , Xnm),} удовлетворяющий условиям:

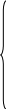
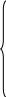
(1) (2)

… … … … … … … … … …

x_ij0 i=1,2,3, …, n j=1,2,3, … m

Минимизируется целевая функция:

Z=C₁₁X₁₁+C₁₂X₁₂+C_1nX_1n+C₂₁X₂₁+C₂₂X₂₂+…+C_2nX_2n+…+C_nmX_nm

Условие (1) означает что груз должен быть полностью вывезен из всех пунктов отправления, смысл условий (2) и (3) состоит в том что заявки всех потребителей должны быть удовлетворены полностью.

Рассматриваемая задача называется ТЗ по критерию стоимости, поскольку в ней ищется план перевозок, минимизирующий суммарную их стоимость.

УСЛОВИЕ ЗАДАЧИ

Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы располагаются в Харькове, Одессе, Донецке, Луцке с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Киеве, Ровно, Львове, Суммах и Днепропетровске с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в табл.1.

Таблица 1. Транспортные расходы

Транспортные расходы	Киев	Ровно	Львов	Суммы	Днепропетровск
Харьков	1,5	2	1,75	2,25	2,25
Одесса	2,5	2	1,75	1	1,5
Донецк	2	1,5	1,5	1,75	1,75
Луцк	2	0,5	1,75	1,75	1,75

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы. Поскольку транспортная задача сбалансирована (суммарный объём произведенной продукции равен суммарному объёму потребностей в ней), то в этой задаче не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции.