Приклад 5. Монтажні напруження в стержньовій системі

Розглянемо визначення монтажних напружень на прикладі вище проаналізованої стержневої системи. Припустимо, що перший стержень виготовлений коротшим на величину . Після зборки системи виникають реактивні зусилля, а тверде тіло займе проміжне положення (рис. 2.4).

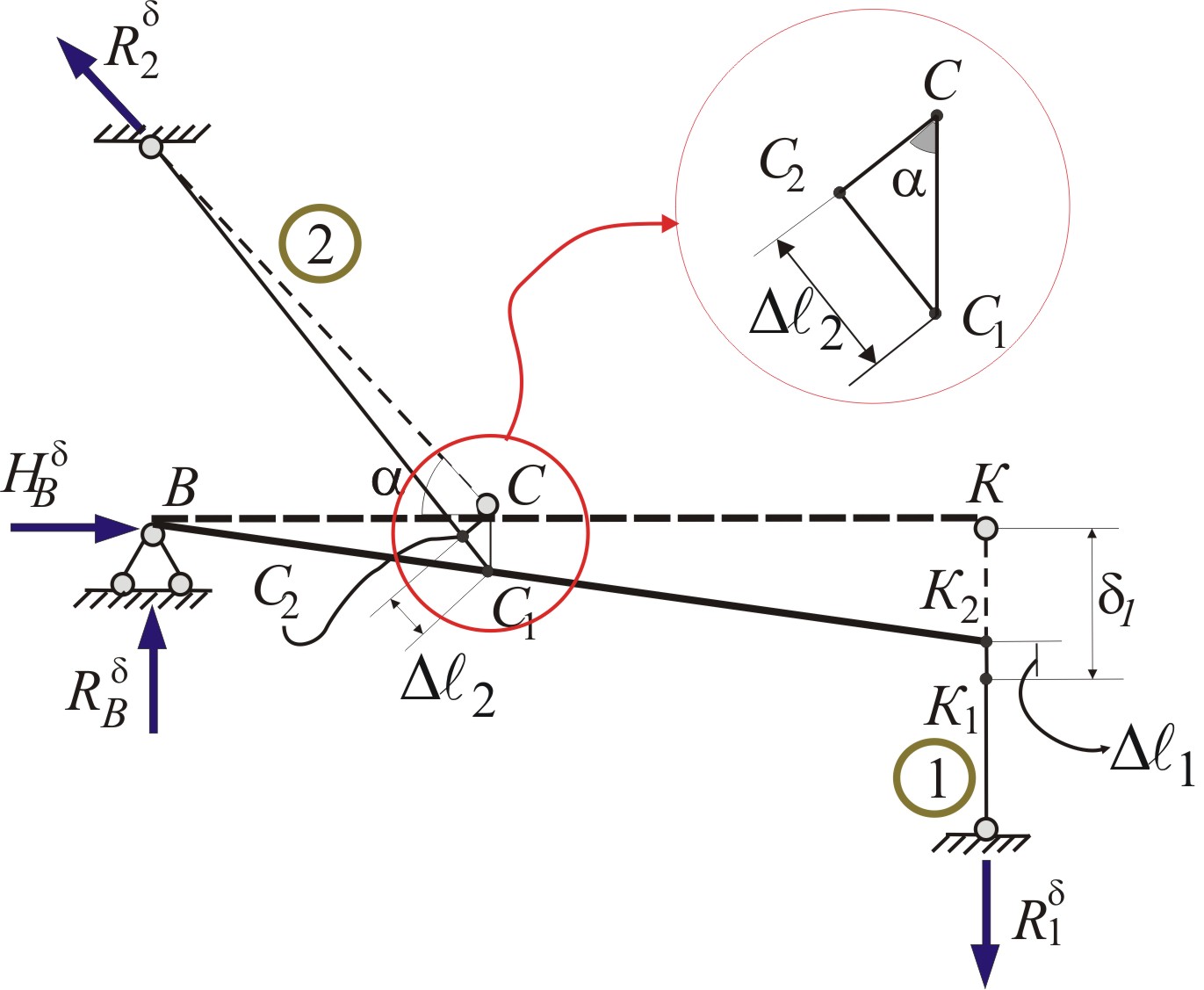
Рис.2.4. Деформована схема

З аналізу деформованої схеми (рис. 2.4) випливає, що стержні подовжуються, в них виникають розтягуючі зусилля та , у шарнірно нерухомій опорі виникають реакції і .

Враховуючи метод перерезів внутрішні зусилля виражаються через реактивні та .

1.ССЗ.

(2.13)

(2.14)

. (2.15)

2.ГСЗ.

З подоби трикутників і маємо:

.

З огляду на те, що

, ,

,

, одержуємо:

.

Тоді рівняння спільності переміщень приймає вигляд:

(2.16)

3.ФСЗ. З огляду на закон Гука у формі: та, підставляючи ці рівняння в умову (2.16), одержуємо

(2.17)

4.Аналіз.

Вирішуючи спільно рівняння (2.17) і (2.15), маємо:

(2.18)

Поздовжня сила визначається з рівняння (2.15).

Монтажні напруження обчислюємо за формулами:

,

У випадку коли перший стержень виготовлений довшим, чим це потрібно ( ), розрахункові схемі залишаються ідентичними, але зусилля та напруження будуть стискаючими.

Приклад 6. Визначення температурних напружень в стержньовій системі

Допустимо перший стержень нагрівається на . Використаємо такий спосіб. Від’єднуємо перший стержень, нагріємо його до заданої температури . При цьому він подовжується на . У нагрітому стані зберемо систему (рис.2.5). Після зборки системи в стержнях виникають реактивні зусилля та , а тверде тіло займає проміжне положення . З аналізу деформованої схеми (рис. 2.5) випливає, що стержні укорочуються, в них виникають стискаючі зусилля та , у шарнірно нерухомій опорі виникають реакції і .

Враховуючи метод перерезів внутрішні зусилля виражаються через реактивні та .

1.ССЗ.

(2.19)

(2.20)

. (2.21)

2.ГСЗ.

З подоби трикутників і маємо: .

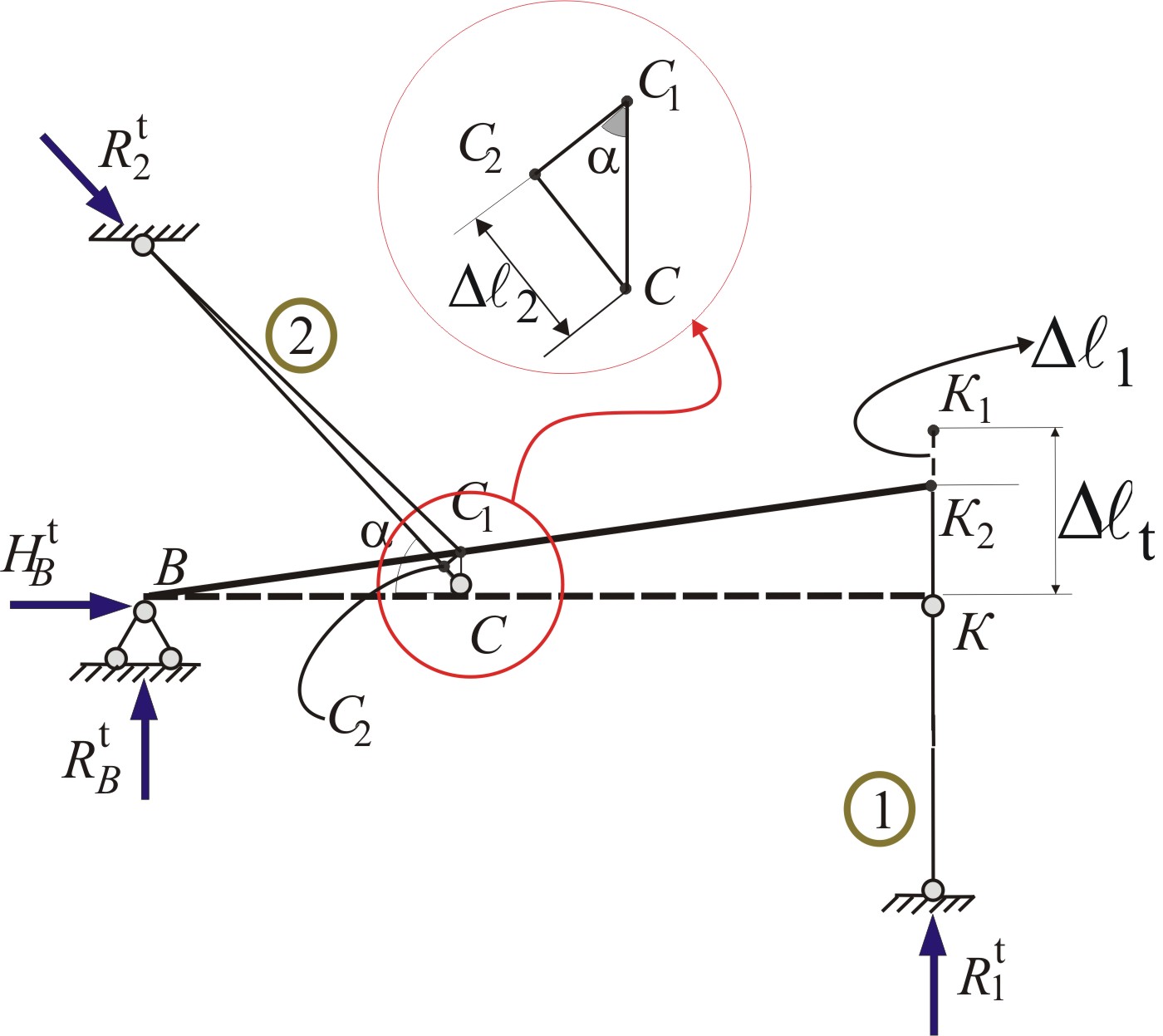
Рис. 2.5. Розрахункова та деформована схеми.

З огляду на те, що

,

, ,

,

, одержуємо:

,

або рівняння спільності переміщень приймає вигляд:

(2.22)

3.ФСЗ. З огляду на закон Гука у формі: та, підставляючи ці рівняння в умову (2.22), одержуємо

(2.23)

4.Аналіз.

Вирішуючи спільно рівняння (2.23) і (2.21), маємо:

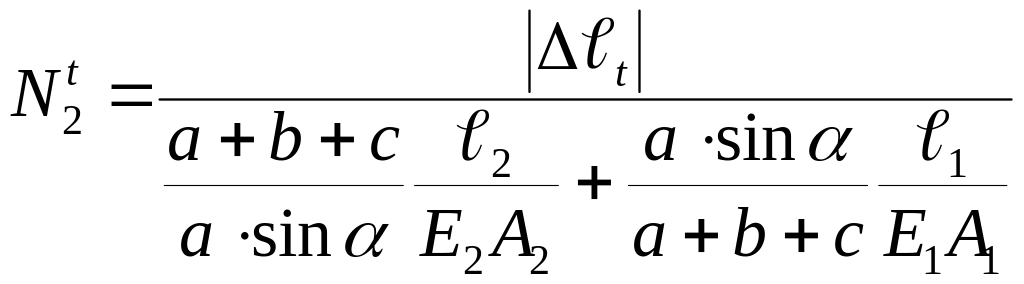(2.24)

Поздовжня сила визначається з рівняння (2.21).

Напруження від зміни температури першого стержня обчислюємо за формулами:

,

У випадку коли перший стержень охолоджується ( ), розрахункові схемі залишаються ідентичними, але зусилля та напруження будуть розтягуючими.