
- •§1. Системы любых уравнений: определения, геометрическая трактовка, равносильность, основные методы решения
- •§2. Некоторые приёмы решения систем нелинейных уравнений
- •1. Исключение одной неизвестной в простейшем случае, когда в системе есть линейное уравнение
- •2. Преобразование системы с целью получить линейное уравнение.
- •3. Введение вспомогательной неизвестной (частичная замена неизвестных)
- •4. Полная замена неизвестных
- •5. Симметричные системы
- •6. Использование однородного уравнения в системе
- •7. Графическое решение систем с целью определения количества решений
5. Симметричные системы
Симметричными называются системы, в которых есть симметрия по неизвестным х и у, то есть система не изменяется, если в ней х заменить на у, а у заменить на х.
Для таких систем рекомендуется специальная замена неизвестных:
![]() .
.
ПРИМЕР
Решим систему уравнений
 .
.
Решение
Данная система является симметричной по х и у, так как при замене х на у, а у на х ни первое, ни второе уравнения системы не изменяются. Используем рекомендуемую замену:
![]() .
.
Тогда в данной системе происходит полная замена неизвестных и получается система, равносильная данной , относительно неизвестных u,v:
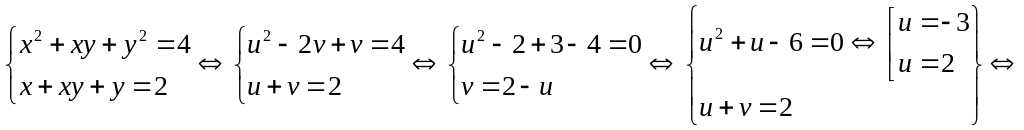
 Система
имеет два решения.
Система
имеет два решения.
Проверка:
![]()
![]()
Заметим, что решения симметричных систем тоже являются симметричными.
Ответ:
![]() ,
,
![]() .
.
6. Использование однородного уравнения в системе
Выражение
![]() называется
однородным по х и у, если оно
представляет собой многочлен, в каждое
слагаемое которого входят только целые
неотрицательные степени переменных х
и у и их суммарная степень одна и та
же во всех слагаемых.
называется
однородным по х и у, если оно
представляет собой многочлен, в каждое
слагаемое которого входят только целые
неотрицательные степени переменных х
и у и их суммарная степень одна и та
же во всех слагаемых.
Например, однородными являются следующие
многочлены:
![]()
![]()
![]() .
.
Уравнение называется однородным,
если оно имеет вид
![]() ,
в котором
– это однородное выражение по х и
у.
,
в котором
– это однородное выражение по х и
у.
Например, однородными являются следующие
уравнения:
![]() ,
,
![]() ,
,
![]() .
.
Однородное уравнение всегда имеет
тривиальное решение
![]() .
.
Другие его решения можно найти, если в этом уравнении перейти к отношению неизвестных делением обеих частей равенства на у2.
ПРИМЕРЫ
1. Решим систему
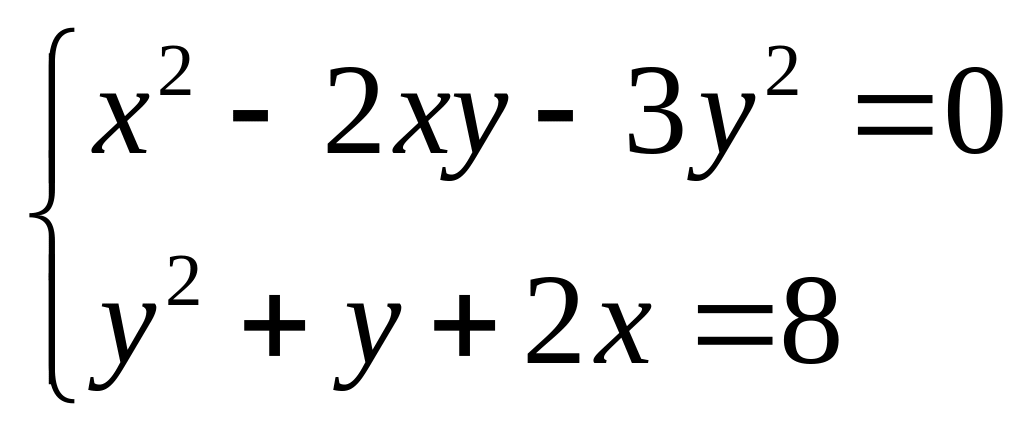 .
.
Решение
Первое уравнение системы является однородным по неизвестным х и у.
Поработаем с ним отдельно, записав сначала его тривиальное решение, а затем разделив обе части уравнения на :
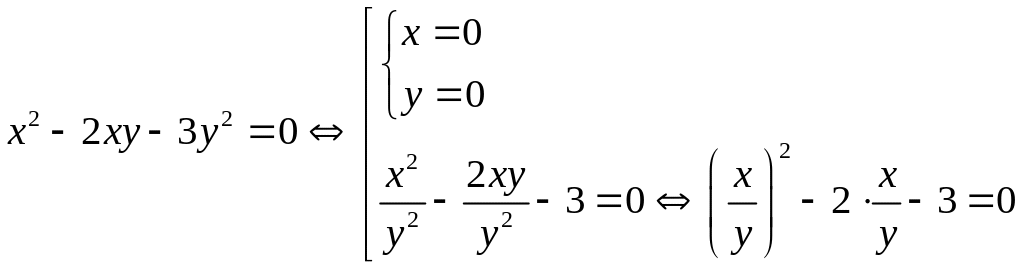 ,
,
переходом к отношению неизвестных
получили квадратное уравнение относительно
этого отношения
![]() ;
решаем это квадратное уравнение:
;
решаем это квадратное уравнение:
![]() ,
,
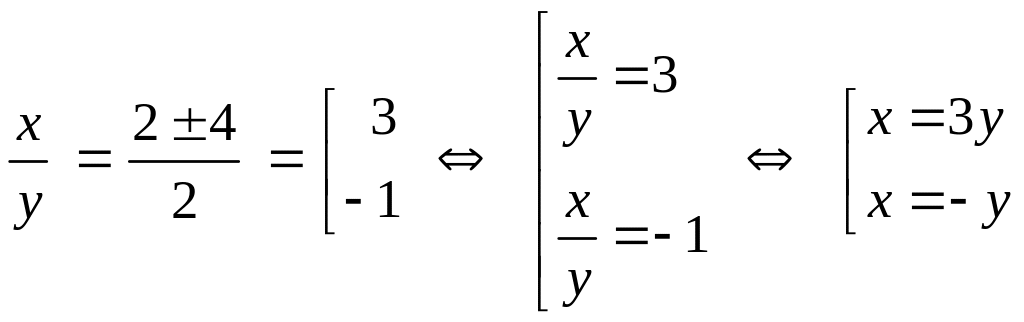 .
.
Возвращаемся в исходную систему, используя результаты работы с однородным уравнением:

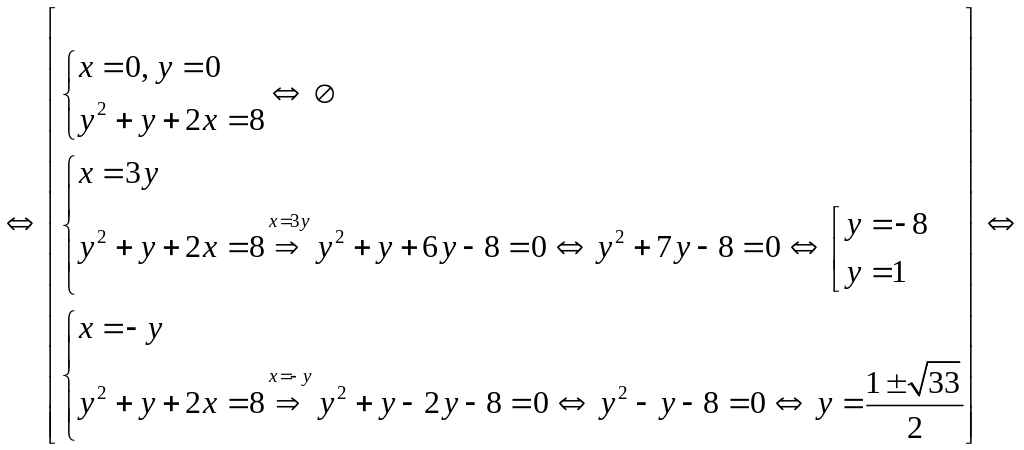

Всего система имеет четыре решения, которые подтверждаем проверкой, подставляя каждое решение в исходную систему.
Проверка:
![]()
![]()
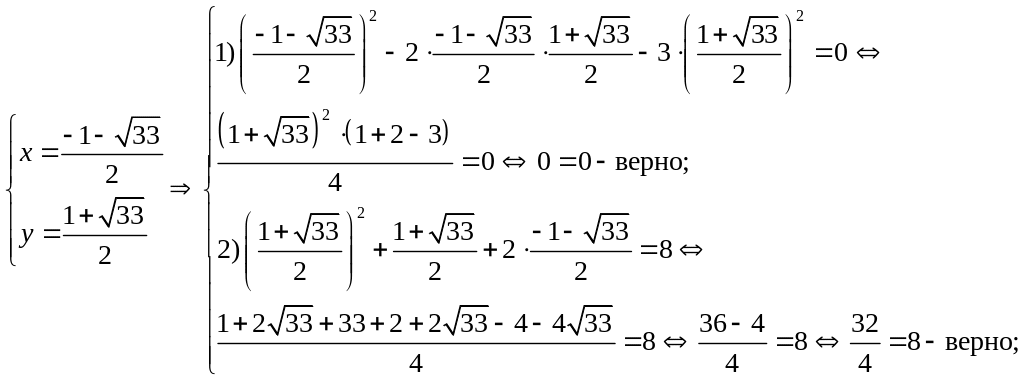

Ответ:
![]() ,
,
,
,
 ,
,
 .
.
2. Решим систему
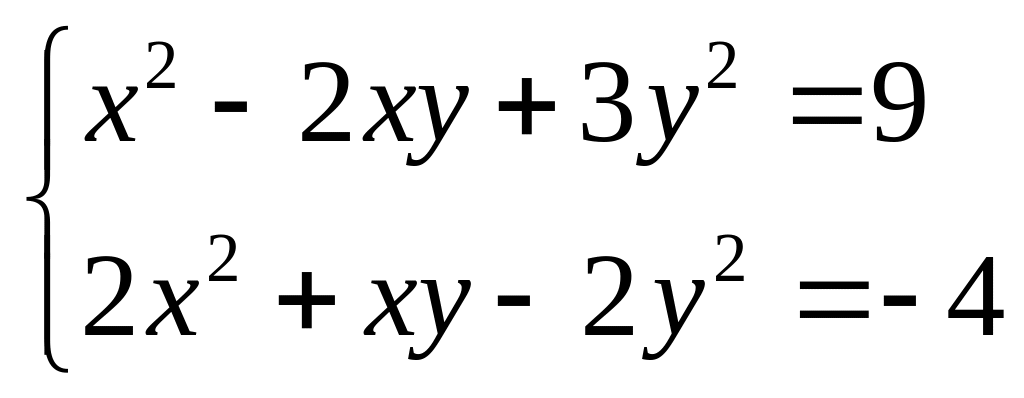 .
.
Решение
В данной системе можно получить однородное уравнение, если алгебраическим сложением уравнений получить уравнение с правой частью, равной нулю:
![]()
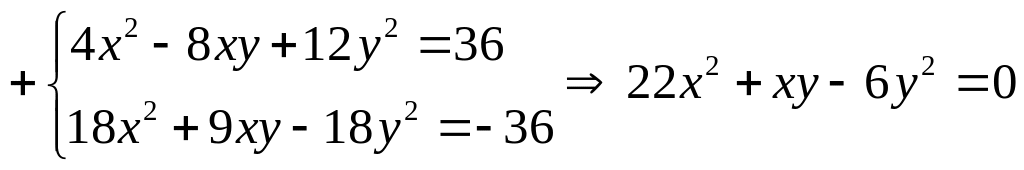 – однородное уравнение.
– однородное уравнение.
Чтобы в пару к однородному уравнению получить более простое уравнение, сделаем ещё одно алгебраическое сложение уравнений с целью исключить произведение ху:
![]() .
.
В результате данная система заменится на равносильную систему, в которой есть однородное уравнение:
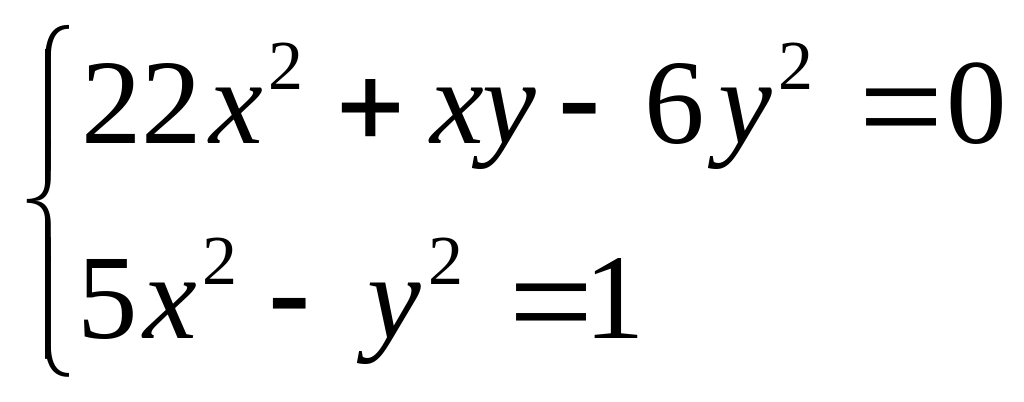 .
.
Тривиальное решение однородного уравнения второму уравнению системы не удовлетворяет, поэтому это тривиальное решение можно не рассматривать, а перейти в однородном уравнении сразу к отношению делением обеих частей уравнения на .
В результате вновь получаем систему, равносильную данной:
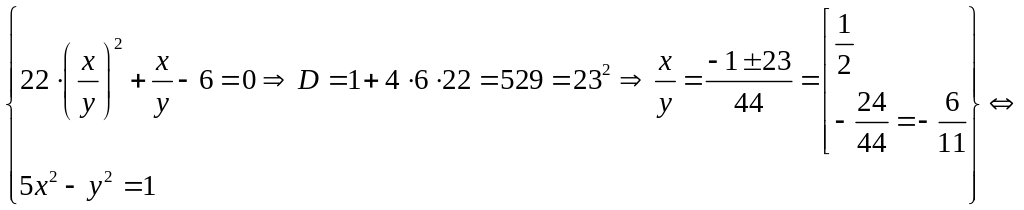


Система имеет 4 решения, подтверждаемых проверкой.
Ответ:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
