
- •Предисловие
- •Общие требования к оформлению расчетной и курсовой работы
- •2. Краткие сведения из теории
- •Момент силы относительно точки и оси
- •Момент силы относительно оси
- •3. Равновесие плоской произвольной системы сил
- •3.1. Равновесие одного тела
- •Расчетная работа №1 Равновесие тела, которое может опрокидываться
- •3.2.Равновесие связанных (сочлененных) тел
- •Равновесие сочлененных тел
- •4. Равновесие пространственной системы сил
- •Условия равновесия произвольной пространственной системы сил
- •Расчетная работа №4 Равновесие пространственной системы сил
- •Исходные данные к расчетной работе № 4
- •Варианты 15, 16, 19, 20, 23, 24
- •Исходные данные к расчетной работе №4
- •Варианты 18, 21, 22
- •Исходные данные к расчетной работе №4
- •Варианты 25, 26, 27
- •5. Центр тяжести твердого тела
- •5.1. Определения, свойства и координаты центра тяжести
- •3.2. Методы нахождения центра тяжести
- •Центр тяжести однородных плоских фигур и линий
- •Исходные данные к расчетной работе № 5
- •Образец оформления титульного листа
- •Статика Расчетная (курсовая) работа
- •Предисловие……………………………………………………………… 3
- •Фигур, линий и объемных тел………………………………………..
Варианты 18, 21, 22
Прямоугольная фрамуга ABCD
веса G удерживается
под углом
![]() к горизонтальной (вар.18)
и к вертикальной (вар.21,
22) плоскости посредством веревки,
перекинутой через блок М, и натягивается
грузом Q и силами
реакций в точках A и
B. Определить при
равновесии вес груза Q
и силы реакций шарниров в точках A
и B, если к фрамуге
приложена сила
к горизонтальной (вар.18)
и к вертикальной (вар.21,
22) плоскости посредством веревки,
перекинутой через блок М, и натягивается
грузом Q и силами
реакций в точках A и
B. Определить при
равновесии вес груза Q
и силы реакций шарниров в точках A
и B, если к фрамуге
приложена сила
![]() .
Необходимые линейные размеры, углы,
величины сил приведены в табл.
4.3.
.
Необходимые линейные размеры, углы,
величины сил приведены в табл.
4.3.
Т а б л и ц а 4.3
Исходные данные к расчетной работе №4
№ схемы |
Линейные размеры, м |
Величины сил, Н |
Углы, |
Примечание |
||||
Н1 |
Н2 |
G |
F |
|
|
|
||
18 |
0,2 1,2 1,4 |
0,5 0,6 0,6 |
25 30 30 |
30 40 30 |
30 60 30 |
– – – |
60 60 30 |
плоскости
|
|
||||||||
21 |
1,4 1,2 1,2 |
0,6 0,5 0,5 |
30 30 25 |
30 25 20 |
60 30 40 |
30 30 30 |
30 60 30 |
параллельна
плоскости
|
|
||||||||
22 |
1,5 1,4 1,2 |
0,8 0,6 0,5 |
40 30 30 |
30 2520 |
60 60 30 |
30 15 60 |
30 30 60 |
лежит
в плоскости
|
|
||||||||
Варианты 25, 26, 27
Горизонтальный вал трансмиссии АВ,
веса G , несущий два шкива
С и D ременной
передачи (плоскость шкивов параллельна
пл. Ayz.), может вращаться
в подшипниках А и В. Радиусы
шкивов
![]() расстояния шкивов от подшипников a
и b; расстояние
между шкивами a+b
(вар. 25) и a
(вар. 26).
расстояния шкивов от подшипников a
и b; расстояние
между шкивами a+b
(вар. 25) и a
(вар. 26).
Вар. 25: натяжения ветвей ремня,
надетого на шкив C,
![]() и
и
![]() вертикальны и имеют
величины
вертикальны и имеют
величины
![]() и
и
![]() ,
причем
=2
;
натяжения ветвей
,
причем
=2
;
натяжения ветвей![]() ,
,
![]() ремня, надетого на шкив D,
горизонтальны и имеют величины
ремня, надетого на шкив D,
горизонтальны и имеют величины
![]() и
и
![]() ,
причем
,
причем
![]() кН.
кН.
Вар. 26: натяжения ветвей
ремня, надетого на шкив C,
вертикально, а
образует с вертикалью
угол
![]() ,
причем
=2
;
натяжения ветвей ремня
,
,
надетого на шкив D,
образуют с горизонталью угол
,
причем
=2
;
натяжения ветвей ремня
,
,
надетого на шкив D,
образуют с горизонталью угол
![]() и имеют величины
и
,
причем
и имеют величины
и
,
причем
![]() кН. Предполагая, что опоры (цилиндрические
подшипники) А и В не оказывают
осевого давления, и пренебрегая весами
шкивов C и D,
определить натяжения
кН. Предполагая, что опоры (цилиндрические
подшипники) А и В не оказывают
осевого давления, и пренебрегая весами
шкивов C и D,
определить натяжения
![]() и
и
![]() в условиях равновесия и реакции
подшипников C и
D, вызванные натяжением
ремней. Необходимые линейные размеры,
углы, величины сил помещены в табл. 4.4.
в условиях равновесия и реакции
подшипников C и
D, вызванные натяжением
ремней. Необходимые линейные размеры,
углы, величины сил помещены в табл. 4.4.
Вар.27: Горизонтальный вал АВ,
несущий два шестерни С и D,
может вращаться в подшипниках А и
В. Радиусы шестеренок
расстояния шестеренки С от подшипника
А a,
шестеренки D от подшипника
B c
; расстояние между шестеренками
b. Плоскости
шестеренок параллельны плоскости
.
К шестеренкам С и D
приложены по направлению касательной
тангенциальные
(горизонтальные) усилия
,
соответственно, по направлению нормали
радиальные
(горизонтальные) усилия
![]() и
и
![]() ,
причем
=
3
,
причем
=
3![]() ,
,
=0.5
кН;
![]() =
1,5
=
1,5![]() .
Предполагая, что в подшипниках А и
В не возникают осевые усилия, и
пренебрегая весами шестеренок и весом
вала, определить
.
Предполагая, что в подшипниках А и
В не возникают осевые усилия, и
пренебрегая весами шестеренок и весом
вала, определить
а) усилия и , приложенные к шестерне D в условиях равновесия, и реакции подшипников А и В.
б) радиальную и тангенциальную составляющие
силы давления на шестерню С в точке
E, считая, что
![]() кН.
Необходимые линейные размеры, углы,
величины сил помещены в табл. 4.4.
кН.
Необходимые линейные размеры, углы,
величины сил помещены в табл. 4.4.
Т а б л и ц а 4.4
Исходные данные к расчетной работе №4
№ схемы |
Линейные размеры, м |
Величины сил, кН |
Угол, |
||||||
а |
b |
|
|
G |
T2 |
N2 |
|
|
|
25 |
0.2 0.4 0.6 |
0.5 0.6 0.6 |
0.03 0.04 0.05 |
0.04 0.05 0.06 |
3 4 5 |
0.24 0.30 0.36 |
|
|
|
26 |
0.8 1.0 1.2 |
0.6 0.5 0.5 |
0.03 0.04 0.05 |
0.03 0.04 0.05 |
3 4 5 |
0.50 0.60 1.00 |
|
60 30 45 |
30 30 60 |
27 |
0.10 0.15 0.20 |
0.08 0.10 0.12 |
0.20 0.30 0.40 |
0.10 0.15 0.20 |
|
|
О.4 0.5 0.6 |
|
|
Пример 4.1 выполнения расчетной работы №4. Равновесие пространственной произвольной системы сил, приложенной к одному телу.
Дано: Однородная прямоугольная плита ABCD (рис.4.2) веса G закреплена в точке A сферическим, а в точке B - цилиндрическим шарниром и поддерживается в горизонтальном положении тросом CK, расположенным в вертикальной плоскости, проходящей через CD, образующим с вертикалью угол . Размеры плиты указаны на схеме (рис.4.2).
Определить реакции шарниров и натяжение троса.
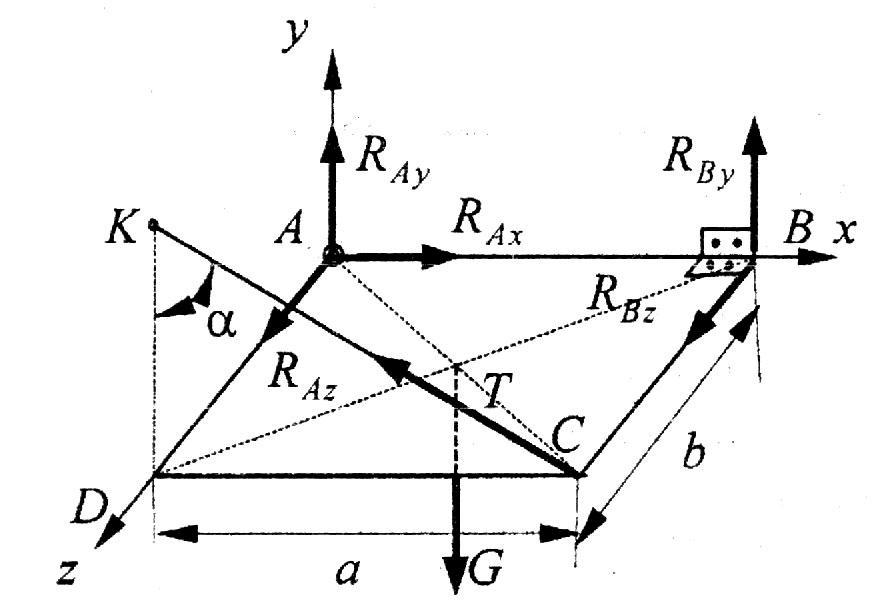 Р
е ш е н и е. Освобождаем плиту от
связей и рассматриваем ее равновесие
под действием заданной силы веса
G, реакций в шарнирах
Р
е ш е н и е. Освобождаем плиту от
связей и рассматриваем ее равновесие
под действием заданной силы веса
G, реакций в шарнирах
![]() ,
,
![]() и натяжения троса
и натяжения троса
![]() .
Поставленную задачу можно записать
коротко следующим образом:
.
Поставленную задачу можно записать
коротко следующим образом:
ABCD
![]() ,
,
.
Задача статически определима, т.к.
число неизвестных (
,
,
,
,
.
Задача статически определима, т.к.
число неизвестных (
,
,![]() ;
;![]() ,
,![]() ,
,![]() )
соответствует числу уравнений равновесия
Рис. 4.2
для пространственной
системы сил, приложенных к плите:
)
соответствует числу уравнений равновесия
Рис. 4.2
для пространственной
системы сил, приложенных к плите:
1.![]()
sin
= 0;
=
sin
= 0;
=
![]() ;
;
2.![]()
G
cos
= 0;
=
G
cos
= 0;
=
![]() ;
;
3.![]()
= 0;
=
=
= 0;
=
= ![]() ;
;
4.![]() G
G
![]()
cos
b = 0;
=
cos
b = 0;
=
![]() ;
;
5.![]()
a
sin
b = 0;
=
;
a
sin
b = 0;
=
;
6.
![]()
G
G
![]()
a
cos
a = 0;
= 0.
a
cos
a = 0;
= 0.
Уравнения равновесия для пространственной системы сил, приложенных к телу, удобно представлять в виде таблицы:
№ |
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
|
0 |
|
2 |
|
|
|
|
0 |
0 |
0 |
3 |
|
0 |
|
|
0 |
a |
a |
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решая полученную систему уравнений,
определяем искомые реакции. По заданным
компонентам определяются реакции
![]() ,
,
![]() .
Направления реакций, имеющих по
результатам расчета знак “ минус”,
противоположны тем, которые указаны на
схеме сил, но изменять ничего не надо.
.
Направления реакций, имеющих по
результатам расчета знак “ минус”,
противоположны тем, которые указаны на
схеме сил, но изменять ничего не надо.
 Пример 4.2. Дано: Однородная
прямоугольная плита ABCD
(рис.4.3) веса G прикреплена
к стене в точке A
сферическим, а в точке B
- цилиндрическим шарниром и удерживается
в горизонтальном положении тросом DK,
закрепленный в точке D
плиты и к гвоздю K,
вбитому в стену на одной вертикали с
шар Рис. 4.3
ниром A и
образующим с AD угол
. Размеры плиты и
действующие нагрузки указаны на схеме
(рис. 4.3).
Пример 4.2. Дано: Однородная
прямоугольная плита ABCD
(рис.4.3) веса G прикреплена
к стене в точке A
сферическим, а в точке B
- цилиндрическим шарниром и удерживается
в горизонтальном положении тросом DK,
закрепленный в точке D
плиты и к гвоздю K,
вбитому в стену на одной вертикали с
шар Рис. 4.3
ниром A и
образующим с AD угол
. Размеры плиты и
действующие нагрузки указаны на схеме
(рис. 4.3).
Определить реакции шарниров и натяжение троса.
Р е ш е н и е. Освобождаем плиту от связей и рассматриваем ее равновесие под действием заданной силы веса G, сосредоточенной силы , реакций в шарнирах , и натяжения троса .
Поставленную задачу можно записать коротко следующим образом:
ABCD , , , .
Задача статически определима, т.к. число
неизвестных (
,
,
;![]() ,
,
)
соответствует числу уравнений равновесия
для пространственной системы сил,
приложенных к плите. Силу натяжения
,
,
)
соответствует числу уравнений равновесия
для пространственной системы сил,
приложенных к плите. Силу натяжения
![]() необходимо
геометрически разложить на три
составляющие:
необходимо
геометрически разложить на три
составляющие:
![]() ,
,
![]() ,
,
![]() и вычислить (см. рис. 4.3)
и вычислить (см. рис. 4.3)
=
![]()
![]() =
=
![]()
=
![]()
=
![]()
1.
+
= 0;
=
+![]() =1.45
кН;
=1.45
кН;
2.
![]()
![]() = 0;
=
+
=
= 0;
=
+
=
= 2.77 кН;
3.
G
![]() +
+
= 0;
=
G +
+
+
= 0;
=
G +
![]() =
=
= 0.67 1.33 кН;
4.
G
+
![]()
a
+
sin
а
= 0;
=
a
+
sin
а
= 0;
=![]() =
=
= 1.33 кН;
5.
G![]() +
b
sin
b
= 0;
=
+
b
sin
b
= 0;
=![]() =6
кН;
=6
кН;
6.
b
a
= 0;
=
![]() =
1.15 кН.
=
1.15 кН.
Уравнения равновесия для пространственной системы сил, приложенных к телу, удобно представлять в табличном виде:
|
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
|
0 |
|
2 |
|
0 |
|
|
|
|
|
3 |
|
|
|
|
0 |
0 |
0 |
4 |
|
|
0 |
|
a |
0 |
a |
5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Решая
полученную систему уравнений, определяем
искомые реакции. По заданным компонентам
определяются реакции
,
.
Направления реакций, имеющих по
результатам расчета знак “ минус”,
противоположны тем, которые указаны на
схеме сил, но изменять ничего не надо.
Решая
полученную систему уравнений, определяем
искомые реакции. По заданным компонентам
определяются реакции
,
.
Направления реакций, имеющих по
результатам расчета знак “ минус”,
противоположны тем, которые указаны на
схеме сил, но изменять ничего не надо.
Пример 4.3 выполнения расчетной работы № 4. Равновесие пространственной произвольной системы сил, приложенной к одному телу (рис.4.4).
Дано: Вертикальный ворот закреплен в точке А подпятником, а в точке В – цилиндрическим шарниром и нагружен так, как это показано на рис. 4.4.
Определить при равновесии силы реакций закрепленных точек, а также натяжение S1 ведущей цепи 1, если S1= аS2, где S2 – натяжение ведомой цепи 2 . Заданы: AO1 = O1O2 = (1/a) AB; AB =1.2 м; r = (b/a)R; R =
= 0.6 м; P =100 H; T1 =100 H; M = 10a Hм; a = 4,
b = 2 безразмерные коэффициенты; углы
=
60,
= 30,
= 30
, образованные радиусами, проведенными
в точке схода цепи (точке касания), с
диаметром колеса, парал Рис.4.4
лельным оси Ay. Поставленную
задачу можно записать коротко следующим
образом: AB![]()
![]()
Решение примера 4.3 (рис.4.4) приведено в виде таблицы:
№ |
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
2 |
|
0 |
0 |
0 |
0 |
0 |
M |
3 |
|
|
0 |
0 |
0 |
AO2 |
r |
4 |
|
|
0 |
0 |
0 |
AO2 |
R |
5 |
|
|
|
0 |
|
|
R |
6 |
|
|
|
0 |
|
|
|
7 |
|
|
|
|
0 |
0 |
0 |
8 |
|
|
|
0 |
AB |
AB |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
