3.1. Равновесие одного тела

Задача на равновесие одного тела под действием плоской произвольной системы сил решается в следующей последовательности:

 выделить тело, равновесие которого рассматривается;

 указать заданные активные силы, приложенные к телу;

 в случае несвободного тела мысленно освобождаем тело от связей, заменив их действием реакций связей (направление которых выбирается исходя из вида связи (табл.2.1);

 составить расчетную схему, указав на ней (на рисунке схемы конструкции) все приложенные к телу активные силы, моменты и реакции связей, распределенные нагрузки замещаются при этом сосредоточенными силами с указанием точек их приложения;

 определить число неизвестных реакций и число возможных уравнений равновесия и установить, является ли рассматриваемая задача статически определимой;

 выбрать систему координат и составить уравнения равновесия;

 решить систему уравнений и определить все неизвестные величины;

 провести качественный анализ полученного решения и его соответствия механическим условиям задачи.

Задачу на равновесие плоской системы сил, приложенной к одному телу, рассматриваем для двух случаев:

Расчетная работа №1. Равновесие тела, которое может опрокидываться;

Расчетная работа №2. Равновесие плоской произвольно расположенной системы сил.

Расчетная работа №1 Равновесие тела, которое может опрокидываться

При выполнении расчетной работы №1 на опрокидывание рассматривается предельное положение, когда тело находится в состоянии неустойчивого равновесия и может перейти из состояния покоя в движение. Всякое даже незначительное изменение элементов конструкции или сил, действующих на тело, ведет к опрокидыванию (вращению) конструкции вокруг некоторой оси, называемой осью опрокидывания. Некоторые активные силы, приложенные к телу, образуют пары, которые стремятся опрокинуть тело. Сумма моментов таких сил относительно оси опрокидывания называется моментом опрокидывания; другая часть активных сил создает пары, которые стремятся возвратить тело в исходное положение. Сумма моментов этих сил относительно оси опрокидывания называется моментом устойчивости.

Определить:  вес противовеса , при котором не произойдет опрокидывание ненагруженного крана;максимальный вес груза, который сможет поднять кран; реакции в опорах крана при максимальной нагрузке.

Схемы конструкций механических кранов представлены на рис.3.1, а

исходные данные: веса кранов, положение центра тяжести C и линейные размеры  в табл 3.1.

Элементы конструкции принимаются абсолютно жесткими, стержневые детали  сплошными и невесомыми, трение в шарнирах и опорах отсутствует.

Пример 3.1 выполнения расчетной работы №1. Равновесие плоской произвольной системы сил, приложенной к одному телу, которое может опрокидываться.

Дано: Механический кран (рис.3.2) веса установлен на горизонтальной поверхности. Расстояние между опорами , абсцисса центра тяжести крана , вылет стрелы крана относительно опоры ,

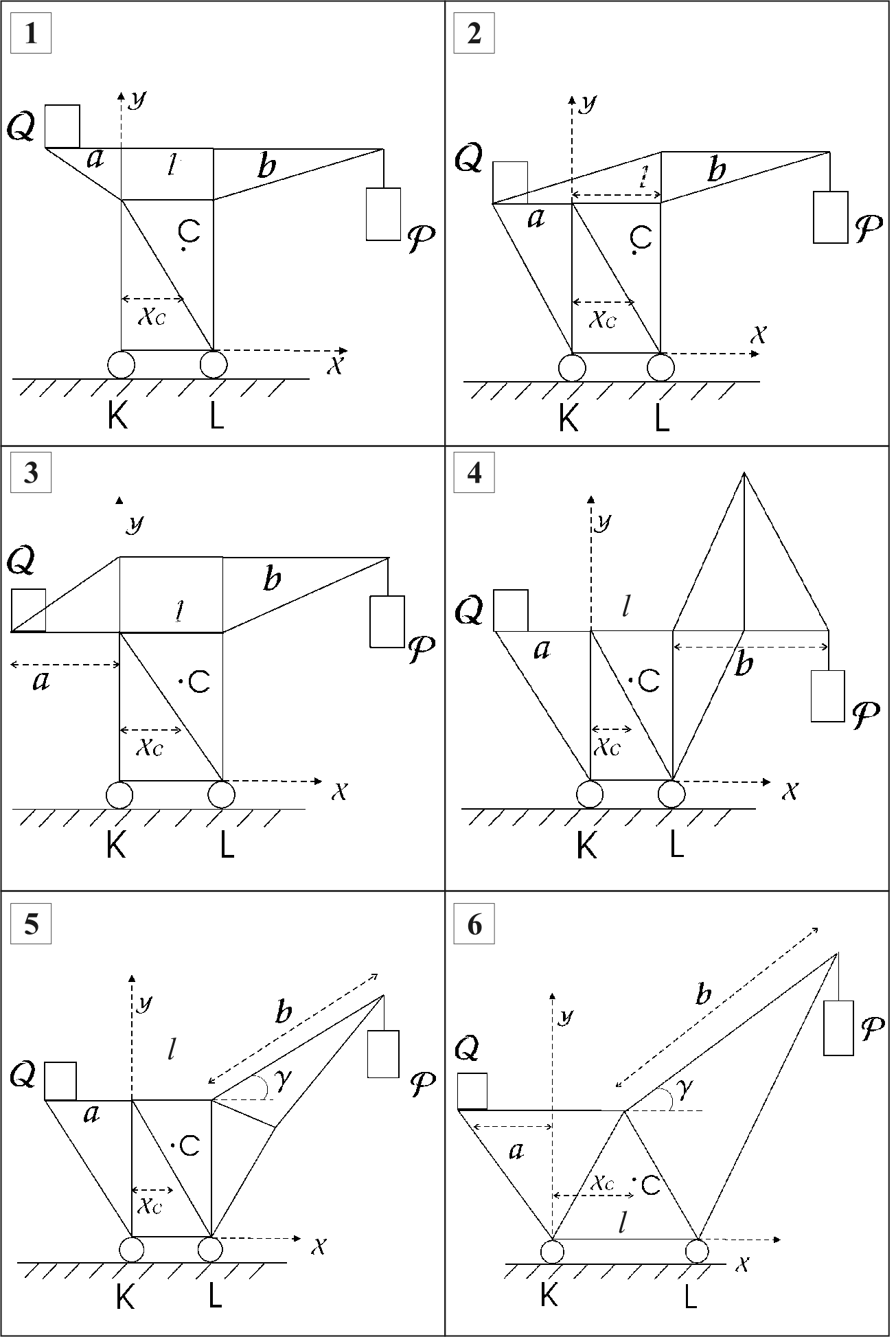
Рис. 3.1. Схемы конструкций механических кранов к расчетной работе № 1

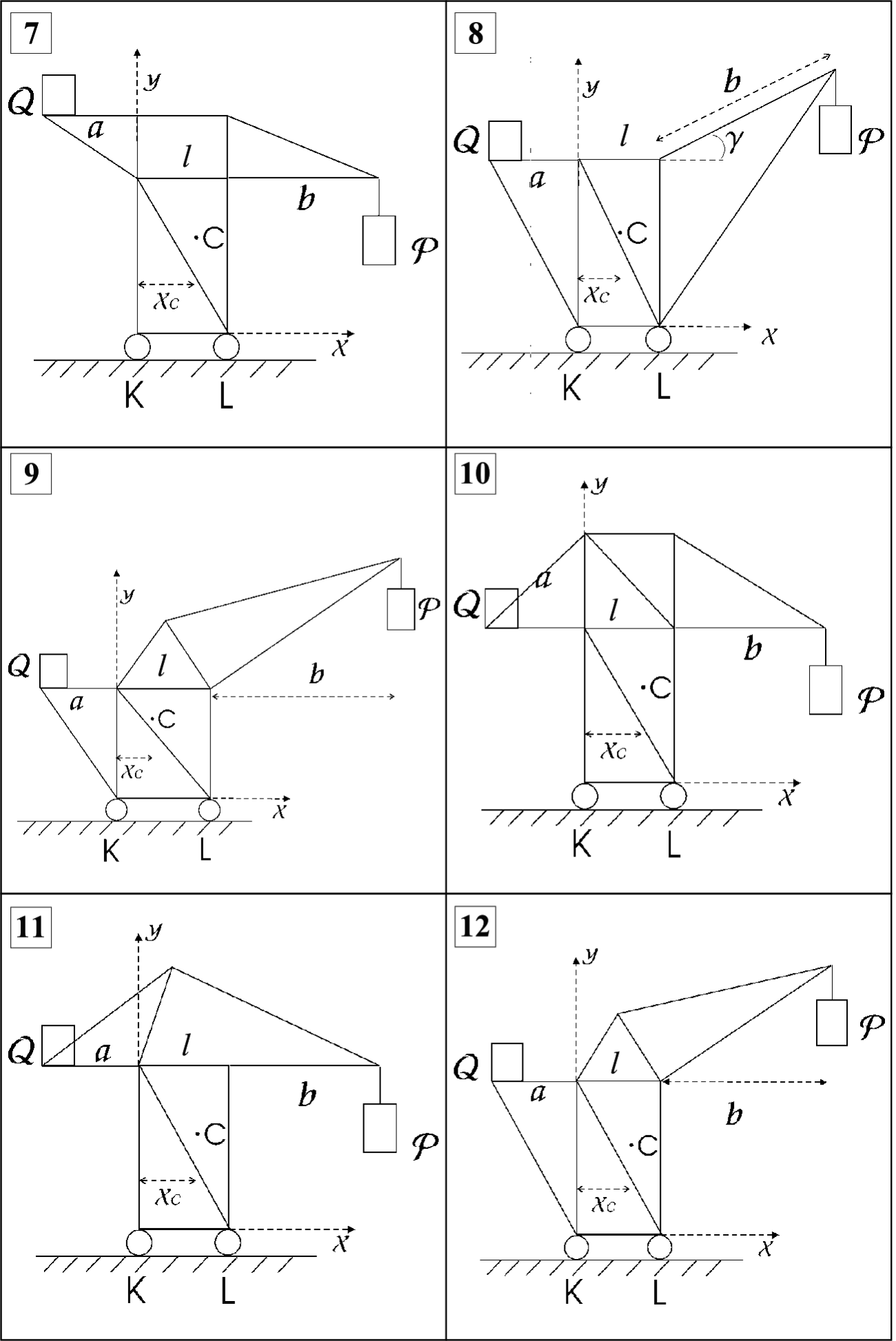
Рис. 3.1 (продолжение)

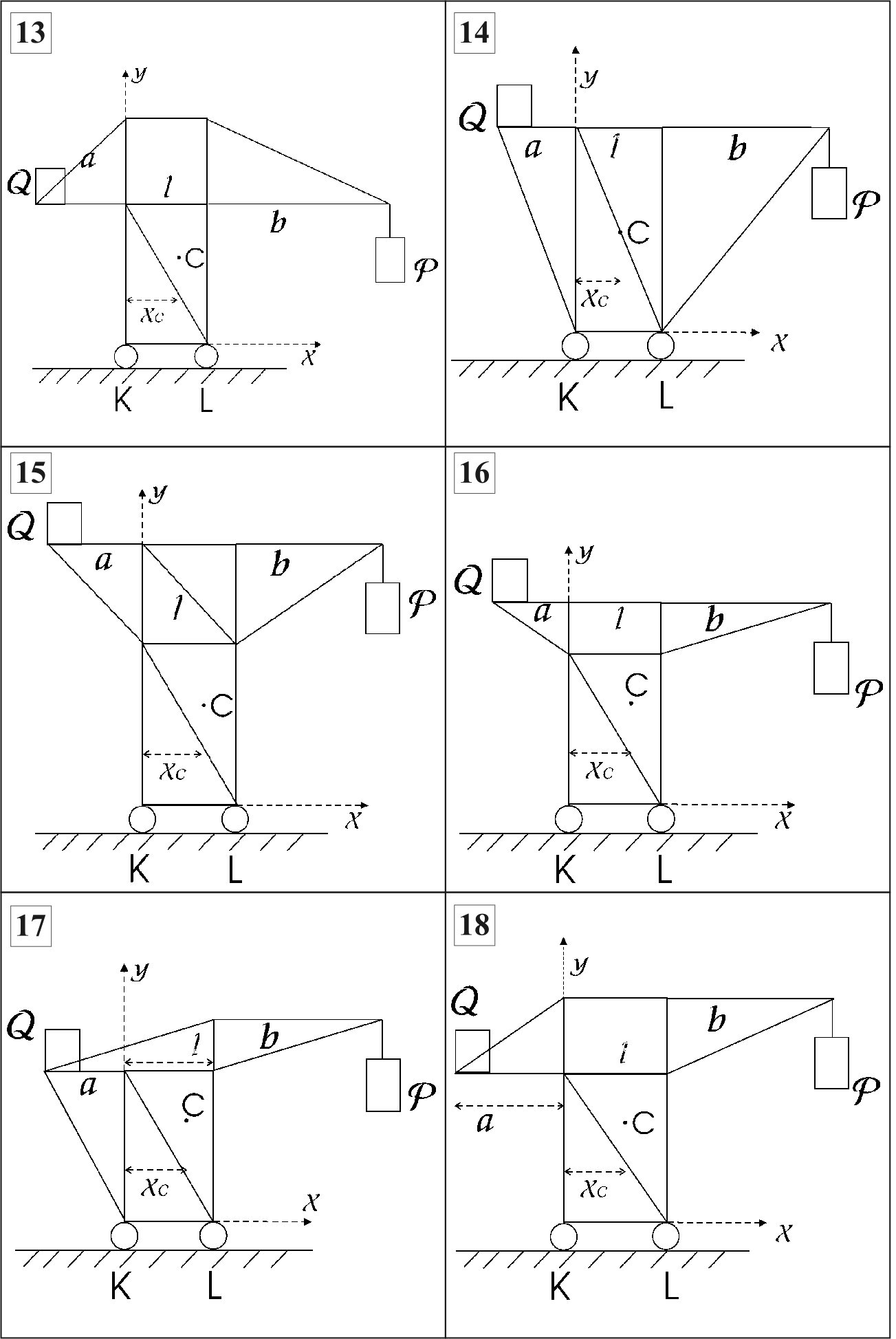
Рис. 3.1 (окончание)

Т а б л и ц а 3.1

Исходные данные к расчетной работе №1

№ схе- мы	Линейные размеры, м			Координата центра тяжести, м	Угол, град	Вес крана, кН
	a	b	l	xC		G
1	0,8 1,0 1,2	2,2 2,5 3,0	1,6 2,0 2,4	0,64 0,80 0,96	– – –	35 40 44
2	1,2 0,8 1,0	3,0 2,0 2,5	2,4 1,6 2,0	0,48 0,32 0,40	– – –	60 50 50
3	0,6 0,4 1,4	1,5 1,0 3,5	1,2 0,8 2,8	0,12 0,08 0,28	– – –	60 62 56
4	1,6 1,8 2,0	4,0 4,5 5,0	3,2 3,6 4,0	3,2 3,6 4,0	– – –	45 44 35
5	1,4 0,6 0,4	3,5 1,5 1,0	1,2 0,8 0,6	0,42 0,18 0,12	60 45 30	36 40 42
6	3,4 4,0 3,5	4,5 5,0 4,0	3,6 4,0 3,2	0,36 0,46 0,58	30 35 30	32 36 40
7	0,7 0,9 1,1	1,75 2,25 2,75	1,4 1,8 2,2	0,14 0,30 0,45	– – –	42 45 50
8	0,5 1,3 1,5	1,25 3,75 3,75	0,4 1,2 1,3	0,15 0,39 0,45	– – –	30 34 32

Продолжение табл. 3.1

№ схе- мы	Линейные размеры, м			Координата центра тяжести, м	Угол, град	Вес крана, кН
	a	b	l	xC		G
9	1,7 1,9 1,0	4,25 4,75 2,50	1,6 1,5 1,8	0,51 0,57 0,26	– – –	30 34 32
10	1,1 1,9 0,9	0,85 1,22 0,68	0,5 0,6 0,4	0,32 0,25 0,45	– – –	45 44 46
11	1,5 1,3 0,5	3,10 2,62 1,05	2,2 1,9 1,2	0,22 0,11 0,34	– – –	30 35 32
12	1,2 1,9 1,7	3,10 4,75 4,25	2,44 3,80 3,40	0,24 0,38 0,34	– – –	42 45 44
13	0,8 0,6 1,4	2,20 1,70 3,70	1,76 1,36 2,96	0,76 0,56 1,20	– – –	34 35 30
14	1,4 0,8 0,6	3,72 2,25 1,76	2,96 1,76 1,36	0,30 0,18 0,14	– – –	40 45 44
15	1,0 1,5 2,0	4,76 3,65 4,60	2,10 1,42 2,15	0,22 0,35 0,65	– – –	50 48 46

Окончание табл. 3.1

№ схе- мы	Линейные размеры, м			Координата центра тяжести, м	Угол, град	Вес крана, кН
	a	b	l	xC		G
16	0,8 1,0 1,2	2,2 2,5 3,0	1,6 2,0 2,4	0,64 0,80 0,96	– – –	35 40 44
17	1,2 0,8 1,0	3,0 2,0 2,5	2,4 1,6 2,0	0,48 0,32 0,40	– – –	60 50 50
18	0,6 0,4 1,4	1,5 1,0 3,5	1,2 0,8 2,8	0,12 0,08 0,28	– – –	60 62 56

расстояние относительно опоры K, на котором должен располагаться противовес для обеспечения максимальной грузоподъемности крана, равно .

Решение. Рассмотрим равновесие крана (рис.3.2). К нему приложены активные заданные силы: вес крана , вес груза и вес противовеса . На кран наложены д ве связи  катковые опоры K, L, которые не допускают смещения крана вниз от опорной поверхности по вертикали, но не препятствуют его повороту вокруг точек K, L. Так как трением в опорах пренебрегаем, то реакции опор будут направлены нормально к поверхности.

Теперь рассматриваем равновесие крана как свободного тела, находящегося под действием сил , .

Опрокидывание ненагруженного крана под действием противовеса возможно вокруг левой опоры K в направлении против часовой стрелки, при этом кран правой опорой L только касается поверхности, не оказывая на нее никакого давления. Поэтому вес противовеса находится из условия равенства моментов опрокидывания и устойчивости

, откуда = .

Максимально загруженный кран может опрокидываться вокруг правой опоры L по часовой стрелке. Поэтому уравнение моментов составим относительно точки L.

Из полученного уравнения находим наибольший вес поднимаемого груза

=27 кН.

Для определения реакций в опорах крана составим уравнения равновесия для полученной системы сил по третьей форме  два уравнения моментов относительно опор K и L:

Из полученных уравнений находим искомые реакции

РАСЧЕТНАЯ РАБОТА №2

Равновесие плоской произвольно расположенной системы сил

Определить реакции связей.

Схемы конструкций представлены на рис.3.3, исходные данные – в табл. 3.2, где G  сила тяжести, P  активная сила,  равномерно распределенные нагрузки, M  момент.

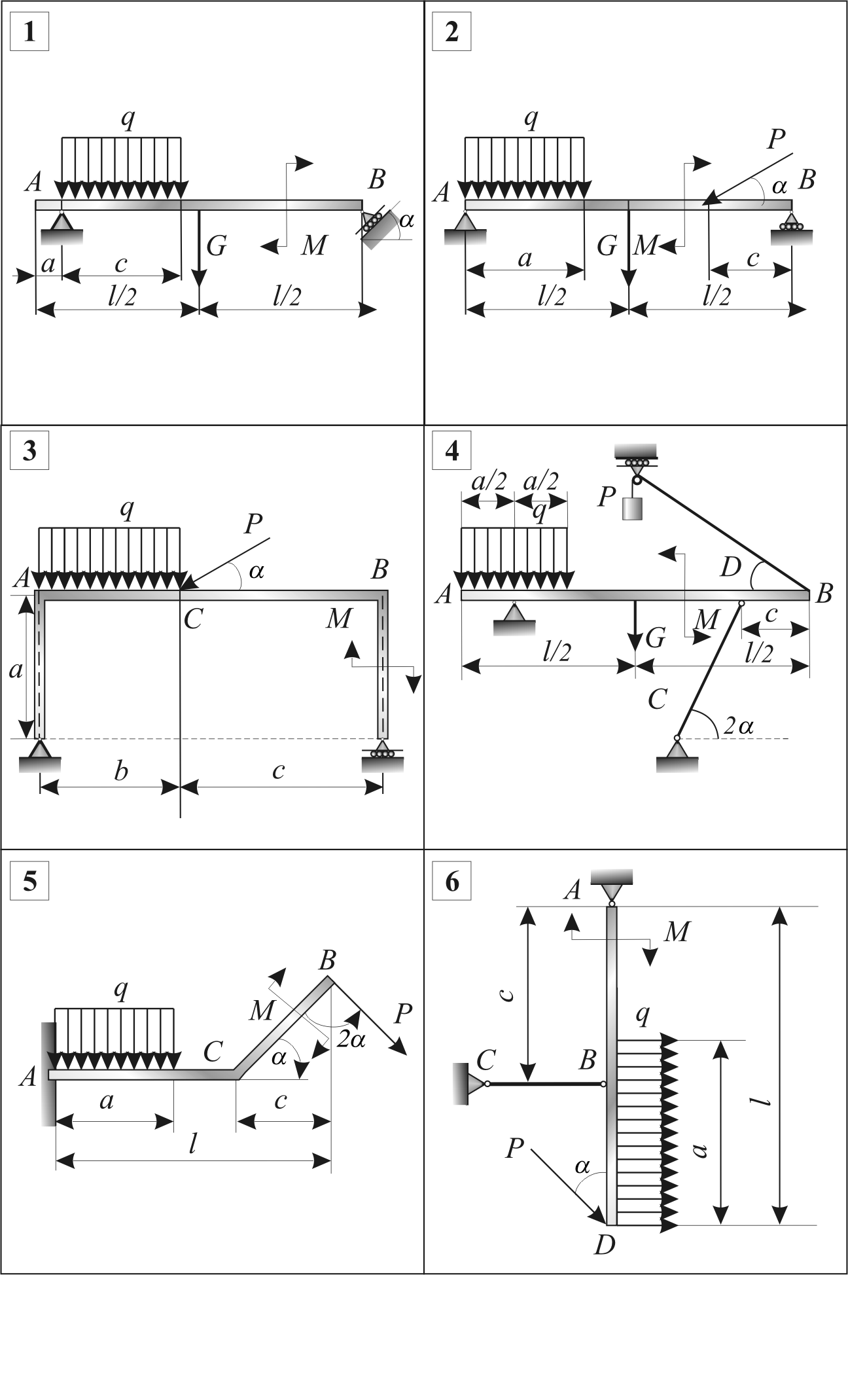
Рис. 3.3. Схемы конструкций к расчетной работе № 2

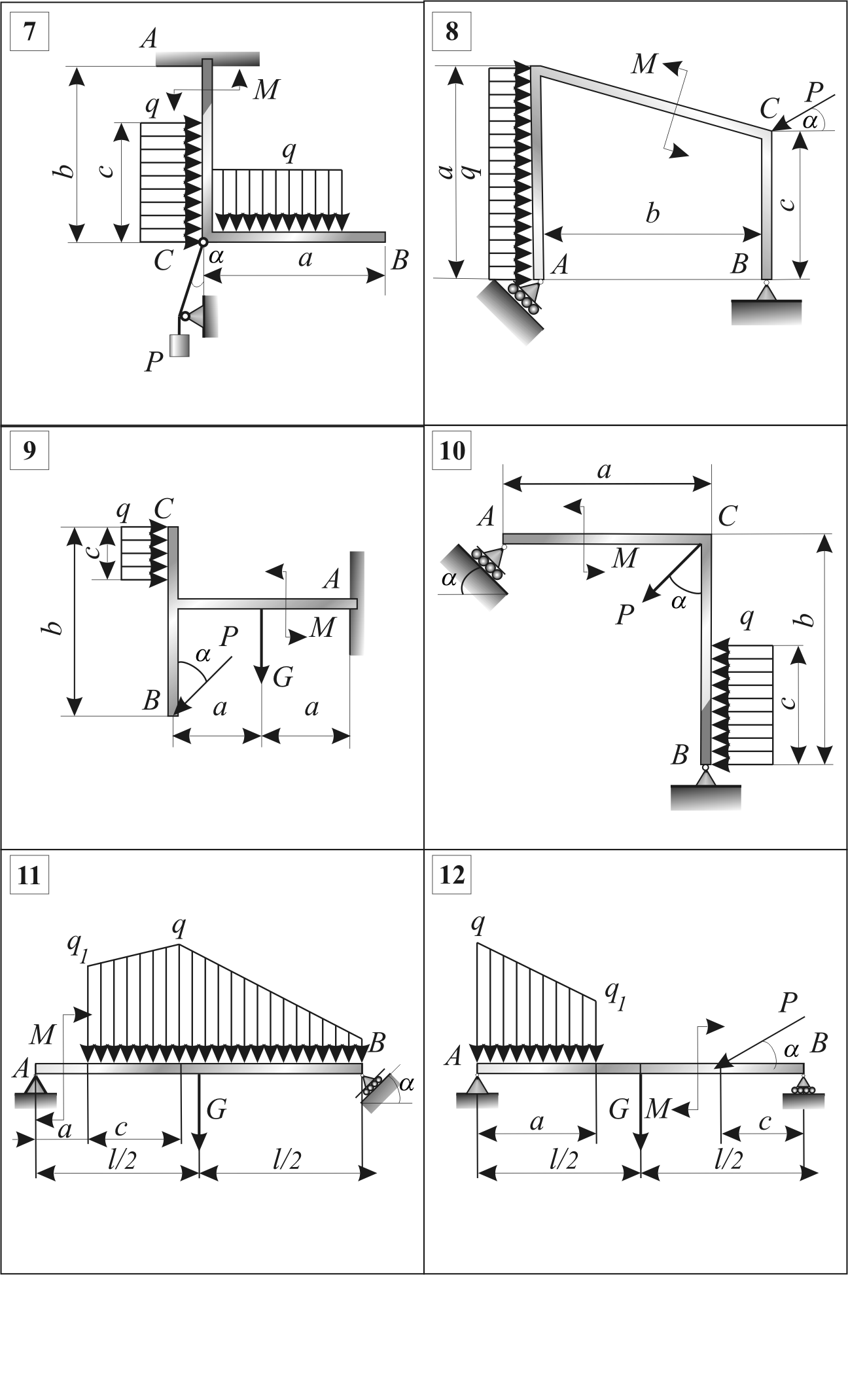
Рис. 3.3 (продолжение)

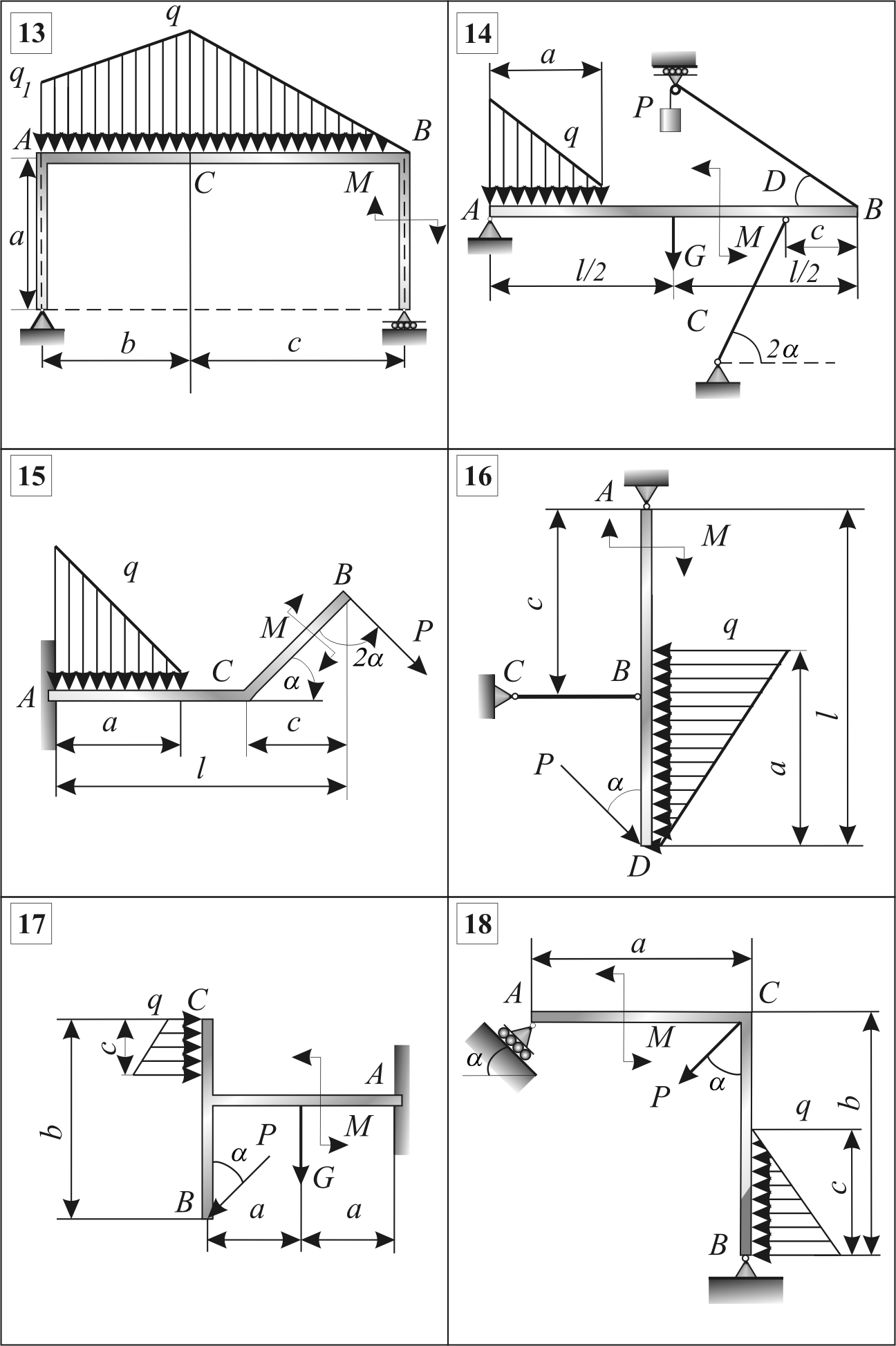
Рис. 3.3 (окончание)

Т а б л и ц а 3.2

Исходные данные к расчетной работе № 2

№ схе- мы	Линейные размеры, м				Угол,  град	G	P		M
	a	b=l	c			кН		кН/м	кНм
1	2 3 3	4 6 6	1 2 3	45 90 30		6 8 4		3 4 5	7 8 9
2	2 3 3	4 6 6	1 2 3	30 45 60		6 8 4	5 6 8	2 3 4	9 8 7
3	2 2 2	4 4 3	1 0 1	30 60 90			2 3 4	4 5 6	9 8 6
4	1 2 2	4 5 5	1 1 2	30 45 60		6 7 8	5 4 6	2 4 6	8 9 6
5	2 5 3	4 10 8	2 4 2	30 45 60			4 5 6	3 4 6	6 7 9
6	3 2 2	4 2 3	3 1 1	30 60 45			6 7 8	2 4 6	8 9 6
7	2 2 3	5 6 8	2 3 3	60 30 45			9 8 7	2 4 6	5 6 8
8	2 4 2	3 5 2	1 2 2	45 60 30			3 4 5	2 4 6	5 8 9
9	2 2 2	4 2 6	1 2 4	30 60 45		4 6 8	5 6 8	4 6 8	8 9 7
10	4 4 3	4 3 4	2 3 3	30 45 60			7 8 9	1 2 4	8 9 7

Окончание табл. 3.2

№ схе- мы	Линейные размеры, м				Угол,  град	G	P		M
	a	b=l	c			кН		кН/м	кНм
11	2 3 3	4 6 6	1 2 3	45 90 30		6 8 4		8 /2 4 /2 6/3	7 8 9
12	2 3 3	4 6 6	1 2 3	30 45 60		6 8 4	5 6 8	6/2 6/3 8/4	9 8 7
13	2 2 2	4 4 3	1 0 1	30 60 90			2 3 4	8/4 6/2 6/3	9 8 6
14	1 2 2	4 5 5	1 1 2	30 45 60		6 7 8	5 4 6	2 4 6	8 9 6
15	2 5 3	4 10 8	2 4 2	30 45 60			4 5 6	3 4 6	6 7 9
16	3 2 2	4 2 3	3 1 1	30 60 45			6 7 8	2 4 6	8 9 6
17	2 2 2	4 2 6	1 2 4	30 60 45		4 6 8	5 6 8	4 6 8	8 9 7
18	4 4 3	4 3 4	2 3 3	30 45 60			7 8 9	1 2 4	8 9 7

Пример 3.2 выполнения расчетной работы № 2. Равновесие плоской произвольно расположенной системы сил. Схема балки показана на рис.3.4.

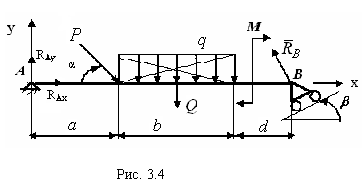Дано: Горизонтальная балка АВ нагружена системой сил: сосредоточенной силой Р = 4 кН, моментом М = 5 кНм пары сил и равномерно распределенной нагрузкой интенсивности q = 2 кН/ м; размеры а = 2м; b=Зм; d=2 м;

углы α =60°; ß =30˚.

Определить: реакции опор и , пренебрегая весом балки АВ.

Решение. Рассмотрим равновесие балки АВ под действием заданных активных сил. Для составления уравнений равновесия необходимо равномерно распределенную по закону прямоугольника нагрузку на заданном участке балки b заменить равнодействующей, равной численно площади заштрихованной фигуры-прямоугольника Q=q·b=2·3=6 кН, и приложенной в центре тяжести этой фигуры.

Освобождаем систему от связей, направив реакцию в катковой опоре (подвижном шарнире В) перпендикулярно плоскости опоры, а реакцию в неподвижном шарнире А заменяем двумя составляющими  .

Поставленную задачу можно записать коротко следующим образом:

AB , .

Так как число неизвестных реакций ( , , ) равно трем, то рассматриваемая задача является статически определимой.

Составим уравнения равновесия плоской системы сил, приложенной к балке АВ:

1. Pcos   sin  + = 0; ;

2.  Psin Q    cos  = 0; ;

3. P a sin   Q  M +   cos  = 0.

Из (3):

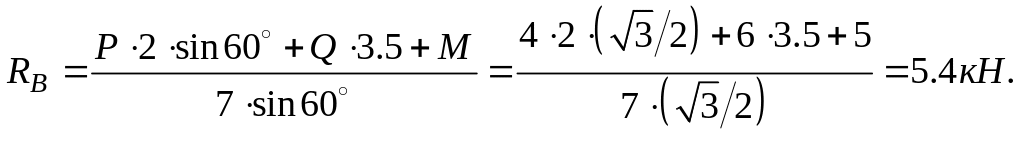
Из (1): =  Pcos +  sin  =  4  0,5+5,4  0,5 = 0,7 kH.

Bp (2): = Psin + Q   cos  = 4 + 6  5.4 = 4,8 kH.

Для проверки полученных значений опорных реакций можно составить дополнительное уравнение равновесия:

 7 + P5sin  + Q 3,5  M = 0;

0=0, значит, реакции определены верно.

Ответ: = 0.7 кН; = 4.8 кН; =5.4 кН.