§ 7. Циркуляция и ротор векторного поля.

Рассмотрим векторное поле

Возьмем в этом поле некоторую кривую L.

- вектор, имеющий направление касательной к

линии L.

Тогда (1)

выражает работу при перемещении материальной точки вдоль линии L.

Если - произвольное векторное поле, а L – замкнутый контур, то интеграл (1) носит специальное название – циркуляция вектора.

Определение. Циркуляцией вектора вдоль замкнутого контура L называется криволинейный интеграл по этому контуру от скалярного произведения вектора на вектор касательной к контуру.

Установим физический смысл циркуляции вектора в случае, когда - поле скоростей текучей жидкости.

Пусть контур L – окружность, расположенная в некоторой плоскости. Предположим, окружность является периферией колесика с радикальными лопатками, могущего вращаться вокруг оси, проходящей через его центр перпендикулярно к его плоскости.

Если циркуляция = 0, то колесико будет оставаться неподвижным: силы, действующие на лопатки, уравновешивают друг друга.

Если циркуляция 0, то колесико будет вращаться, причем тем быстрее, чем больше величина циркуляции.

В случае произвольного векторного поля отношение циркуляции по плоскому контуру L к площади S, ограниченной этим контуром будет величиной переменной.

Вычислим

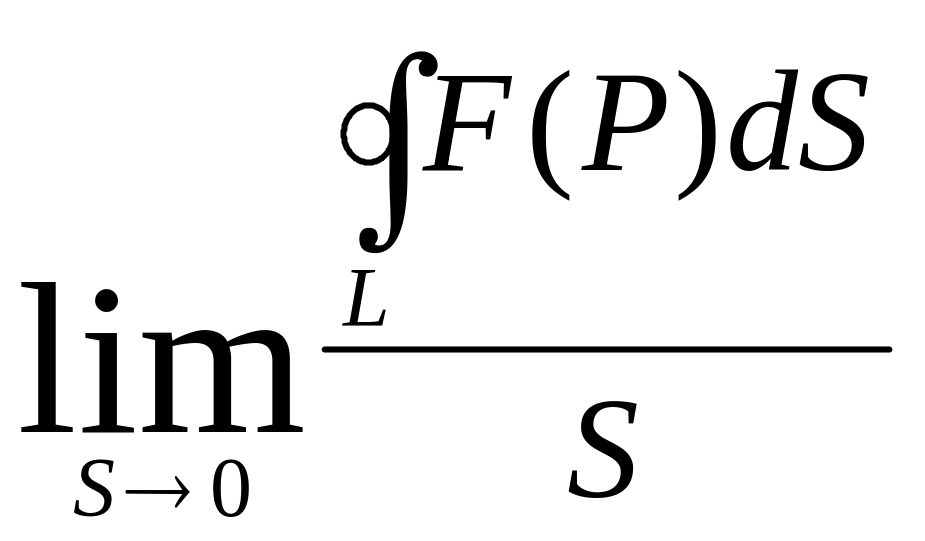
По формуле Стокса

где cos α, cos β, cos γ – направляющие косинусы нормали , а σ – область, ограниченная контуром L. Последний интеграл по теореме о среднем равен произведению подинтегральной функции в некоторой т. Р₁ обл. σ на величину S площади этой области.

Тогда ,

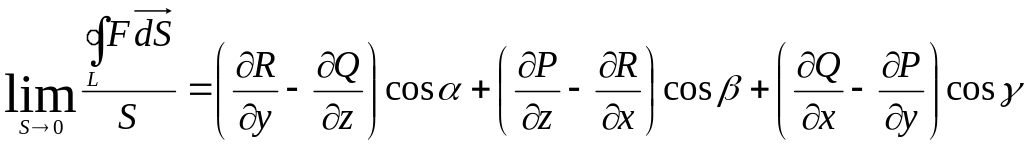где значения всех частных производных берутся в т. Р.

Правая часть представляет скалярное произведение 2^х векторов:

единичного вектора - нормали к плоскости, в которой лежит контур L, и вектора, проекции которого равны

, , .

Последний вектор называют ротором или вихрем векторного поля и обозначают

Тогда формула Стокса принимает вид

Поток ротора поля через поверхность σ равен циркуляции вектора по границе этой поверхности.

Свойства ротора:

1) ,

где С₁, С₂ – постоянные

2)

где u = u(P) – скалярная функция

- векторная функция

Доказать самостоятельно.

Пример. Найти ротор поля

P = x²yz³ Q = -2x²yz³ R = 3x²yz³

§ 8. Оператор Гамильтона и векторные дифференциальные операции второго порядка.

Введенные нами основные понятия векторного анализа: градиент, дивергенция, ротор – удобно представлять с помощью символического вектора («набла-вектор»):

1) Произведение набла-вектора на скалярную функцию u(P) дает градиент этой функции:

2) Скалярное произведение набла-вектора на векторную функцию дает дивергенцию этой функции:

3) Векторное произведение набла-вектора на векторную функцию дает ротор этой функции:

Набла-вектор называют оператором Гамильтона.

Действия взятия градиента, дивергенции и ротора будут векторными дифференциальными операциями первого порядка. В них участвуют только первые производные от скалярных функций.

Перейдем теперь к векторным дифференциальным операциям второго порядка.

Пусть имеется скалярное поле u(P) и мы нашли градиент этого поля grad u. Поле градиента является векторным полем, и мы можем искать его дивергенцию и ротор: div grad u и rot grad u.

Если имеется векторное поле , то оно порождает два поля: скалярное поле и векторное поле . Следовательно мы можем находить градиент первого поля: и дивергенцию и ротор второго поля: и . Всего мы имеем пять векторных дифференциальных операций второго порядка. Особенно важными из них являются три, рассмотрим их.

а)

Действительно

Правая часть называется оператором Лапласа от функции u и обозначается

С помощью набла-вектора можно записать так:

б) с помощью набла-вектора можно записать так:

векторное произведение одинаковых векторов = 0

в) с помощью набла-вектора можно записать так:

Имеем смешанное произведение трех векторов, из которых два вектора одинаковы. В этом случае такое произведение равно нулю.

Остальные две векторные операции второго порядка: и - встречаются реже.