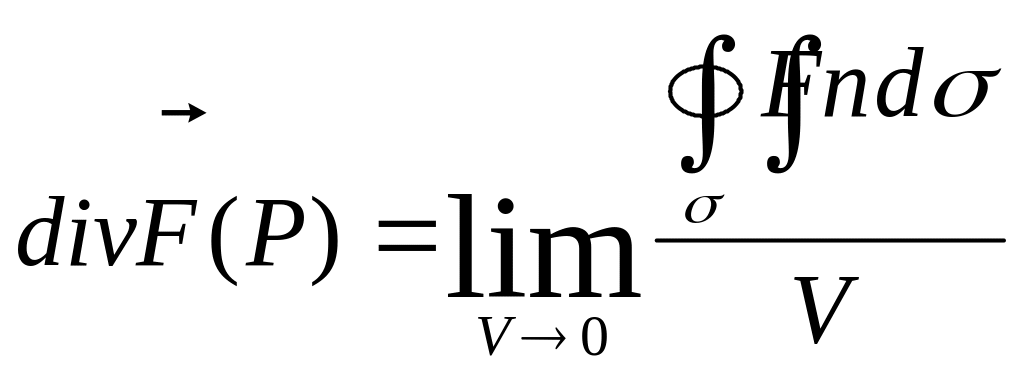§ 5. Дивергенция.

Рассмотрим некоторую т. Р векторного поля и окружим ее замкнутой поверхностью σ, целиком содержащемся в поле.

Вычислим поток вектора через поверхность σ и возьмем отношение этого потока к объему V области V, ограниченной поверхностью σ:

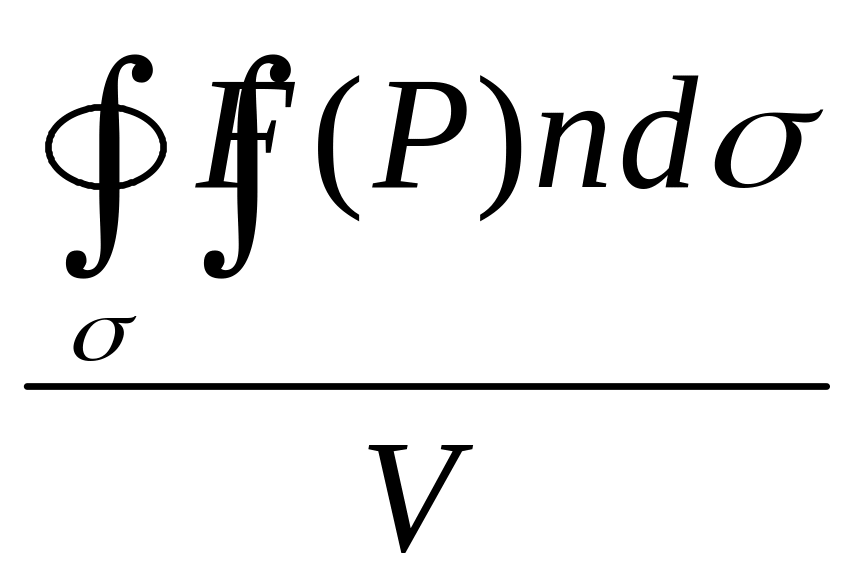
При К>0 это отношение определяет среднюю объемную мощность источника, если поток изнутри поверхности σ меньше нуля, то говорят о мощности стока.

Найдем предел отношения при условии, что область V стягивается в т. Р, т.е.

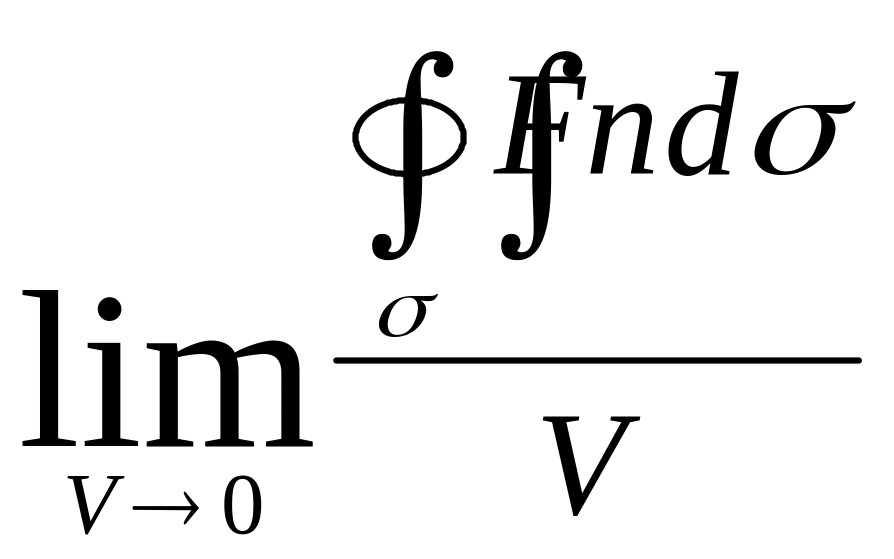
Если этот предел положителен, то т. Р называется источником,

а если отрицателен, то стоком.

Сама величина предела характеризует мощность источника или стока. Предел этот называют дивергенцией или расходимостью векторного поля в

т. Р.

Определение. Дивергенцией, или расходимостью векторного поля в т. Р называется предел отношения потока вектора через поверхность, окружающую т. Р, к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в т. Р.

Обозначают

Теорема. Дивергенция векторного поля

выражается формулой ,

где значения частных производных берутся в т. Р.

Доказательство. По формуле Остроградского

Тройной интеграл по теореме о среднем будет равен

,

где Р₁ – некоторая точка области V, V – объем этой области

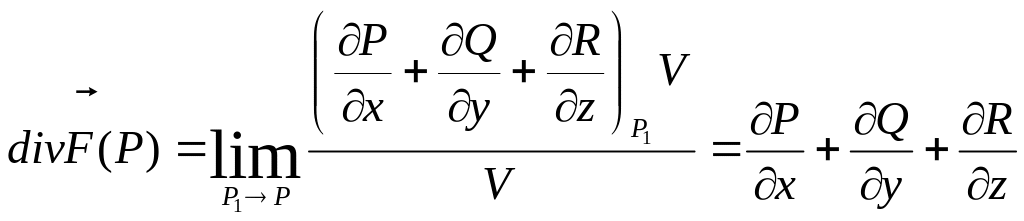
Теорему Остроградского можно записать так:

Теорему можно сформулировать так:

Поток вектора изнутри замкнутой поверхности равен тройному интегралу по объему, ограниченному этой поверхностью от дивергенции поля.

Свойства дивергенции:

1) div ,

Где С₁, С₂ – Const

2) Пусть - векторное поле, u(P) – скалярное поле

div

Доказать самостоятельно.

Пример. Найти дивергенцию поля

в т. М(1, 2, 3)

div

§ 6. Формула Стокса.

Для поверхностных интегралов имеет место формула, позволяющая свести вычисление интеграла по поверхности σ к вычислению криволинейного интеграла по контуру L , ограничивающему эту поверхность.

Теорема Стокса. Если функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны вместе со своими частными производными первого порядка, то имеет место формула

, (*)

где L - граница поверхности σ .

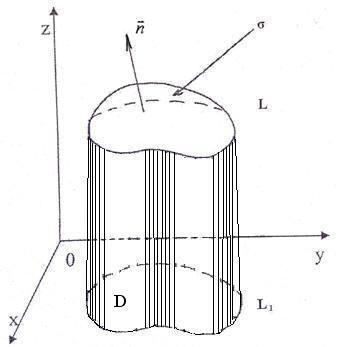
Направление криволинейного интеграла (вдоль L) и поверхностного (по σ) интегрирований согласованы между собой следующим правилом:

е сли человек, идущий по той

z σ стороне поверхности σ, по которой

производится поверхностное

L интегрирование, перемещается

вдоль границы L в направлении

криволинейного интегрирования,

то поверхность должна оставаться

с лева.

0 y

D

x L₁

Формула (*) называется формулой Стокса.

Доказательство. Докажем теорему путем сведения поверхностного интеграла к двойному с последующим применением формулы Грина.

Будем считать, что поверхность σ пересекается с любой прямой, параллельной оси oz не более, чем в одной точке. Тогда уравнение этой поверхности будет z = z (x, y). Интегрирование будем вести по верхней стороне поверхности.

Рассмотрим интеграл

Из формулы определения поверхностного интеграла имеем

где γ и β – углы между нормалью и осями oz, oy

т.к. уравнение поверхности σ: z = z (x,y), то проекциями нормального вектора будут , , -1, Направляющие косинусы пропорциональны этим проекциям, то поэтому .

Значит

Приведем этот интеграл к двойному. z заменим на z(x,y) и

Таким образом, полагая , имеем ,

где D – проекция поверхности σ на плоскость xoy.

Применяя формулу Грина, получим

,

где L₁ – граница области D. Контур L₁ – есть проекция кривой L – границы поверхности σ на плоскость xoy.

Итак, (1)

Аналогично (2)

(3)

Складывая почленно равенства (1), (2), (3) получим формулу Стокса.

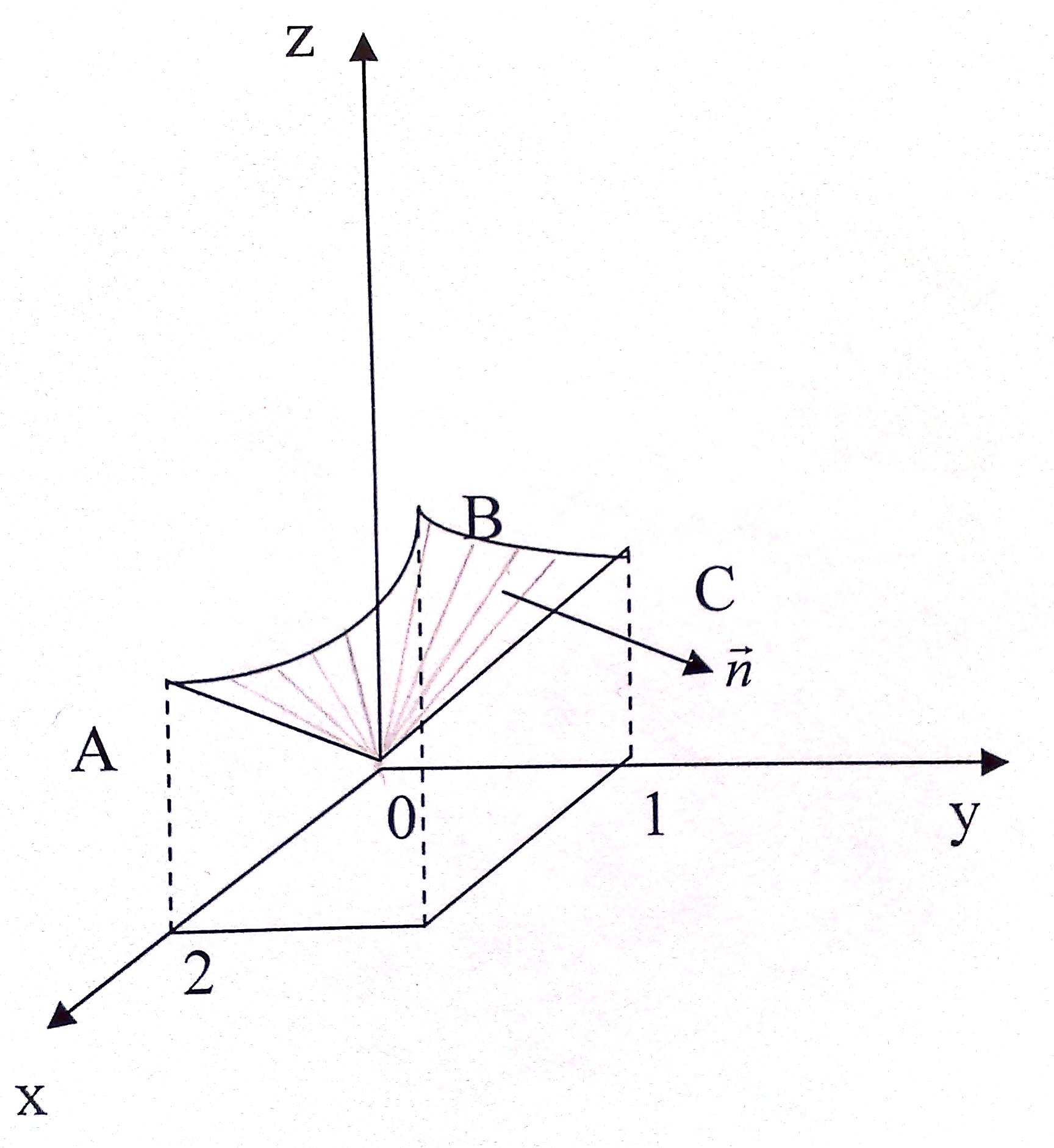
Пример. Вычислить

,

где L – линия пересечения поверхностей

, , , ,

z

В

C

A

0 1 у

По формуле Стокса получим

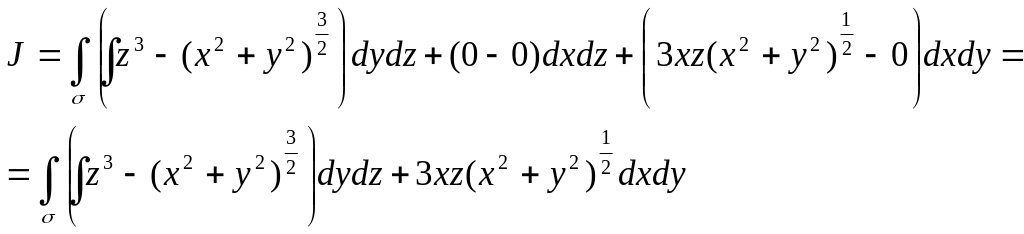
Каждый из них сведем к двойному интегралу

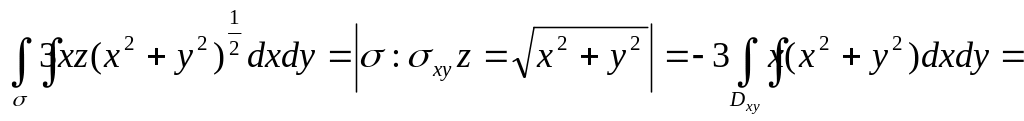
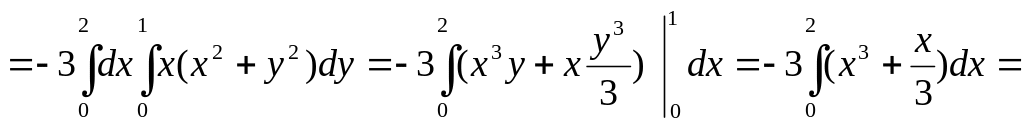
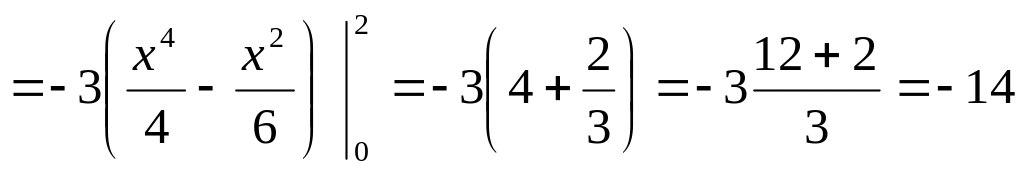
Окончательно J = -14.