Криволинейные интегралы
§ 1. Криволинейный интеграл первого рода.
В трехмерном измерении (т.е. пространство) задана кривая L с концами в т. А и В. Во всех ее точках задана функция ƒ(x, y, z). Разобьем кривую L на n частей точками Ао = А, А1, А2, …, Аn = В.
Пусть
- длина дуги Ак-1Ак.
На каждой дуге Ак-1Ак
берем по
точке (
)
и составим сумму вида
Ее предел при max
∆Sк→0
называют
криволинейным
интегралом первого рода
и обозначают так
Если в частности кривая L лежит в плоскости xoy, то функция ƒ(x, y) зависит от двух переменных и криволинейный интеграл первого рода имеет вид
§ 2. Вычисление криволинейного интеграла первого рода
Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла.
1) Рассмотрим
Пусть кривая L задана параметрически
x = x(t)
y = y(t) α ≤ t ≤ β
дифференциал
Тогда
в правой части равенства определенный интеграл.
Если кривая L задана явно уравнением у = у(x), a ≤ x ≤ b,
то
Пример 1.
Вычислить
,
если
от т. А(1;
)
до т.В (2; 2)
Пример 2: Вычислить
где 
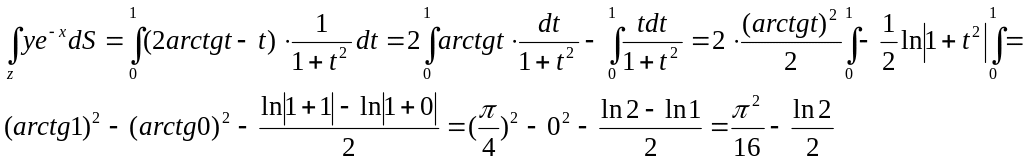
2) Если кривая L пространственная и задана параметрически
α
≤ t ≤ β
то
Пример 3
Вычислить
где
L:
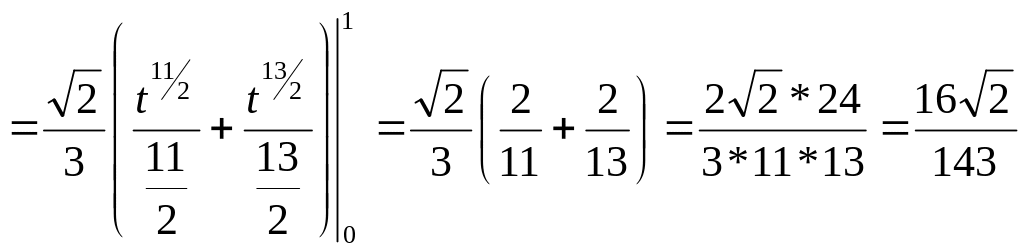
§ 3. Криволинейный интеграл второго рода.
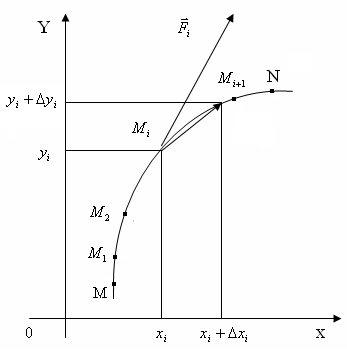
Пусть т. Р(x,y)
движется вдоль некоторой плоской линии
L
от точки М к точке N.
К точке Р приложена сила
,
которая меняется по величине и направлению
при перемещении т. Р вдоль кривой L,
т.е.
представляет
собой функцию координат точки Р.
Вычислим работу А силы при перемещении т. Р из положения М в положение N. Для этого разобьем кривую MN на n частей точками
М0 = М, М1, М2, …, Мn = N
О
бозначим
вектор
,
величину силы
в
т.Мi
через
Тогда
- работа силы
вдоль
дуги
Пусть
,
где P(x, y), Q(x, y) – проекции вектора на оси ox, oy,
а
– скалярное
произведение двух векторов.
Следовательно
Работа А силы на всей кривой MN будет
Существует предел
правой части при
Этот предел называют криволинейным интегралом второго рода и обозначают
или
(М) – читаем т. М, (N) – точка N.
Если кривая L пространственная, то
)