Порядок виконання роботи

1. За допомогою вимірювального мікроскопу визначити діаметр кульки.

2. Опустити кульку в рідину поблизу осі циліндру.

3. По досягненні кулькою верхньої мітки (а) на циліндрі, ввімкнути секундомір, по досягненні нижньої (б) – зупинити секундомір.

4. Виміряти відстань між мітками на циліндрі. Дослід провести для п’яти кульок.

5. Розрахувати коефіцієнт в’язкості рідини для кожного досліду за формулою (4).

Таблиця 1

№ п/п	, м	, м	, с	, Па с
1 2 3 4 5
Сер.

6. Знайти довірчий інтервал: , де - коефіцієнт Стьюдента при n = 5 і p=0.95.

; де .

7. Записати результат у вигляді: при р=0,95;

Контрольні питання.

1. Назвіть явища переносу.

2. Які сили діють на кульку, що падає в рідині?

3. Чому, починаючи з деякого моменту часу, кулька рухається рівномірно?

4. Як змінюється швидкість руху кульки із збільшенням її діаметра?

5. Що називається градієнтом швидкості та як він спрямований?

6. Що таке в’язкість?

7. У яких одиницях вимірюється коефіцієнт в’язкості?

Лабораторна робота №12

ВИЗНАЧЕННЯ СПІВВІДНОШЕННЯ ТЕПЛОЄМНОСТЕЙ ГАЗУ

ПРИ ПОСТІЙНОМУ ТИСКУ ТА ПОСТІЙНОМУ ОБ’ЄМІ

ЗА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА

Теоретичні відомості

Під теплоємністю тіла розуміють кількість теплоти, необхідної для нагрівання цього тіла на 1К. Теплоємність одиниці маси речовини називають питомою теплоємністю. Вводять ще молярну теплоємність – це теплоємність одного моля газу. Молярні теплоємності газів з однаковим числом атомів у молекулі рівні.

Теплоємність газу залежить від умов нагрівання. Розрізняють теплоємність газу при постійному об’ємі С_v та теплоємність при постійному тиску C_p.

Можна показати, що C_p > C_v.

Справді, якщо нагрівати один моль газу на 1К при постійному об’ємі, то надане йому тепло піде тільки на збільшення внутрішньої енергії газу. Якщо ж нагріти газ на 1 К при постійному тиску (тобто надати йому можливість розширюватися), то, крім зазначеної кількості тепла, йому потрібно надати ще деяку кількість тепла, необхідного для виконання роботи розширення:

.

Таким чином, .

Це рівняння називається рівнянням Майера. Для всіх газів, до складу молекул яких входить одна й та сама кількість атомів, величина відношення однакова.

Як показує теоретичний розрахунок, , де - кількість ступенів вільності молекул газу.

Відношення теплоємкостей  входить у вигляді показника ступеня в рівнянні адіабатичного процесу.

Це рівняння називається рівнянням Пуассона і має вигляд

. (1)

Адіабатичним процесом називається процес, що проходить без теплообміну з зовнішнім середовищем. Швидке стискання чи розширення газу можна вважати адіабатичним процесом, тому що за дуже малий проміжок часу теплообмін з зовнішнім середовищем практично не встигає відбутися.

Величина  може бути виміряна експериментально за допомогою методу Клемана-Дезорма.

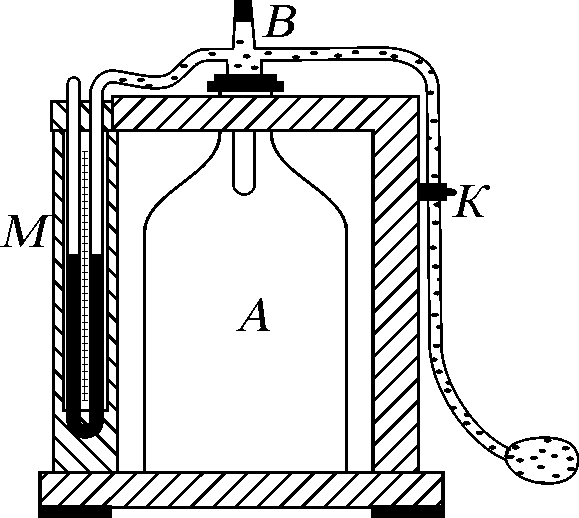
Рис. 1

Прилад для вимірів складається із скляного балона, закритого пробкою, у яку вставлена трубка з отворами, через які балон сполучається з відкритим манометром М і насосом К (рис.1).

При закритому отворі В накачаємо в балон А деяку кількість повітря. Тиск повітря в балоні зросте і стане рівним , де - надлишок тиску повітря в балоні над атмосферним тиском. При накачуванні повітря (що стискається під поршнем насоса) нагрівається, тому необхідно очікувати 2-3 хвилини, поки завдяки теплообміну температура в балоні стане дорівнювати кімнатній. Після цього вимірюють за манометром надлишковий тиск повітря .

Позначимо об’єм посудини та приймемо цей стан за початковий. Він буде характеризуватися об’ємом , тиском та температурою . Потім швидко відчинимо отвір В і закриємо його в той час, коли рівні рідини в манометрі зрівняються при опусканні правого стовпа рідини.

Після цього тиск повітря стане рівним атмосферному , об’єм збільшиться до , а температура понизиться до (другий стан). Цей процес є практично адіабатичним (швидке розширення).

Через якийсь час повітря знову прийме температуру навколишнього середовища , а тиск, унаслідок підвищення температури, зросте до , де - різниця рівнів рідини в манометрі. Слід зазначити, що маса повітря, що залишилася, знаходиться тепер під тиском . Частина повітря, випущена в атмосферу при адіабатичному розширенні, знаходиться під атмосферним тиском . Але тому що ця частина невелика, то ми зневажаємо цією обставиною і вважаємо об’єм газу в третьому стані рівним . Весь хід зміни стану повітря можна показати у вигляді табл.1.

Таблиця 1

Стан газу	Об’єм	Тиск	Температура, 0С
1
2
3

Перехід з першого стану в другий відбувається адіабатично, тому цей процес можна описати рівнянням Пуассона (1):

, відкіля . (2)

У першому та третьому станах температура газу однакова, тому до цих станів можна застосувати закон Бойля-Маріотта , відкіля

.

Зведемо (3) у ступінь 

. (4)

Порівнюючи (2) і (4), одержимо

.

Про логарифмуємо цей вираз:

,

Відкіля

. (5)

Спростимо отриманий вираз, використовуючи ту обставину, що , якщо . Для цього напишемо (5) у вигляді

,

тому що значно менше одиниці (перевищення тиску в балоні над атмосферним значно менше атмосферного тиску), то

чи . (6)

Отримана формула використовується для визначення , тобто задача визначення зводиться до виміру рівнів води в манометрі при різних станах повітря, що знаходиться у балоні.