Глава 3. Сдвиг и кручение стержней

3.1. Понятие о чистом сдвиге. Напряжения и деформации при сдвиге. Закон Гука

На примере растяжения и сжатия были выявлены некоторые наиболее важные свойства напряженного состояния. При растяжении в зависимости от ориентации секущей площадки на гранях выделяемой площадки возникают как нормальные, так и касательные напряжения.

Теперь положим, что имеется такое напряженное состояние, когда на гранях возникают только касательные напряжения . Такое напряженное состояние называется чистым сдвигом (рис.3.1).

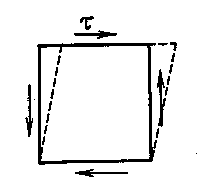
Рис. 3.1

Посмотрим, как при чистом сдвиге изменяются напряжения в зависимости от ориентации секущей площадки.

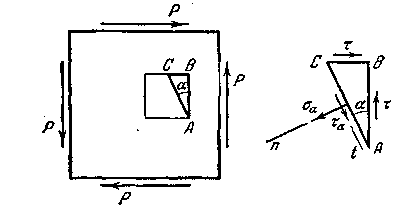
Рис. 3.2

Для этого из пластин, находящихся в состоянии чистого сдвига, выделим элементарную трехгранную призму (рис. 3.2)>.

На гранях и по условию возникают только касательные напряжения. На грани в зависимости от угла возможно возникновение как нормального, так и касательного напряжения. Обозначим их через и . Спроектируем все силы на оси n и t.

,

т.к. и то,

В результате получим

(3.1)

При и а , что соответствует исходным площадкам. При , а .

Следовательно, если выделить прямоугольный элемент грани, который повернут на 45⁰ относительно исходных, то на секущих площадках будут обнаружены только нормальные напряжения, причем на одной паре граней эти напряжения являются растягивающими, а на другой сжимающими. Таким образом, чистый сдвиг может быть представлен как одновременное растяжение и сжатие по двум взаимно перпендикулярным направлениям (рис. 3.3).

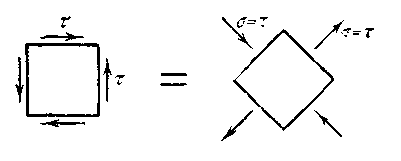
Рис. 3.3

Рассмотрим деформацию элемента ограниченного площадками чистого сдвига (рис. 3.4).

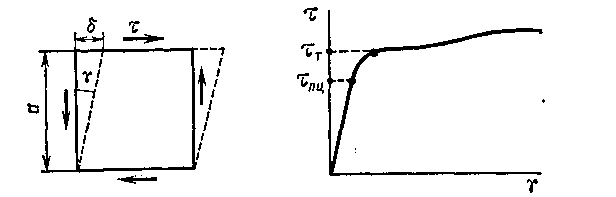
Рис. 3.4

— абсолютный сдвиг

— относительный сдвиг или угол сдвига.

Величина , как показывают эксперименты в пределах напряжений пропорциональности, прямо пропорциональны величине касательных напряжений. Эта зависимость между и , называется законом Гука при сдвиге, выражается в виде

или ,где (3.2)

— модуль сдвига или модуль упругости второго рода. имеет раз-мерность напряжения (для стали Ст.3 ).

Между и существует зависимость . Данная формула показывает, что три постоянных — характерные упругие свойства изотропного материала связаны между собой.

2. Практический расчет соединений работающих на сдвиг

   1. Расчет заклепочных и болтовых соединений

Одним из видов разрушения (рис. 3.5) является срез по сечению а—а.

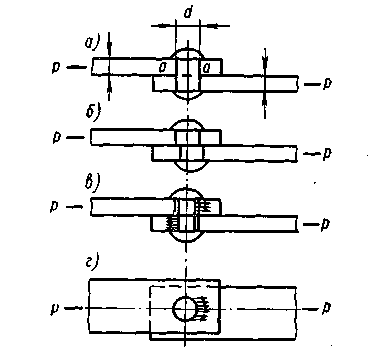
Рис. 3.5

Условие прочности имеет вид , (3.3)

где — расчетное напряжение по площадке сдвига,

— допускаемое касательное напряжение на сдвиг, как правило .

Расчетное напряжение среза, считают условно, равномерно распределенным по сечению .

Если склепываемый пакет содержит больше двух листов, то заклепка может быть двухсрезной (рис. 3.6), трехсрезной и т.п.

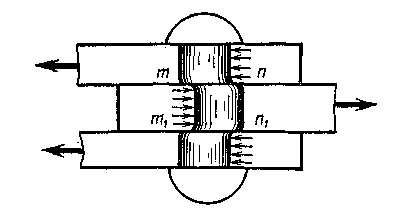
Рис. 3.6

, — число срезов.

Аналогично все это относится к болтовым соединениям. Помимо среза возможно нарушение соединения вследствие смятия листов или заклепок в месте их контакта (рис. 3.7). Фактическое распределение напряжений по поверхности заклепки и листа весьма сложно. Но приближенно опасность смятия может быть оценена не фактической величиной контактных напряжений, а их средним значением, отнесенным к площади проекции контакта на диаметральную плоскость .

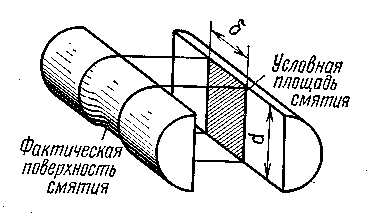
Рис. 3.7

Условие прочности записывается (3.4)

Обычно . Расчетное напряжение определяют по условной площади сжатия .

2. Расчет сварных соединений

Рассмотрим принцип расчета сварного соединения на примере соединения двух листов угловыми швами (рис. 3.8,а).

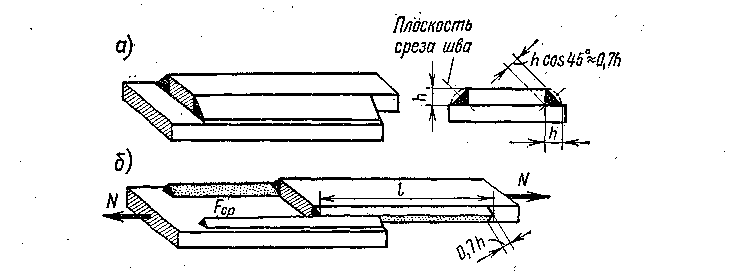
Рис. 3.8

Разрушение швов в рассматриваемом соединении происходит от среза по наименее возможной площади среза, расположенной в биссекторной плоскости прямого угла (рис.3.8,б). При этом расчетное поперечное сечение шва принимается в виде треугольника. Обозначим высоту шва через . При составлении условия прочности предполагается равномерное распределение касательных напряжений по площади среза и шва.

, (3.5)

— допускаемое напряжение.

В зависимости от типа электродов = ,

где — для свариваемого материала.