8. Понятие о деформации тела и о деформации физических точек

Под деформацией тела подразумевается изменения его формы и размеров под действием внешних сил, температуры и т.д. В дальнейшем будем различать деформацию тела в целом и деформацию его бесконечно малых частиц. Деформацию тела в целом будем характеризовать перемещениями его материальных частиц (рис. 1.8,а, б). Произвольная точка в результате деформации тела смещается в некоторое новое положение . Это смещение характеризуем вектором перемещений .

С другой стороны, деформация тела складывается из деформации его материальных частиц (рис. 1.8,в)

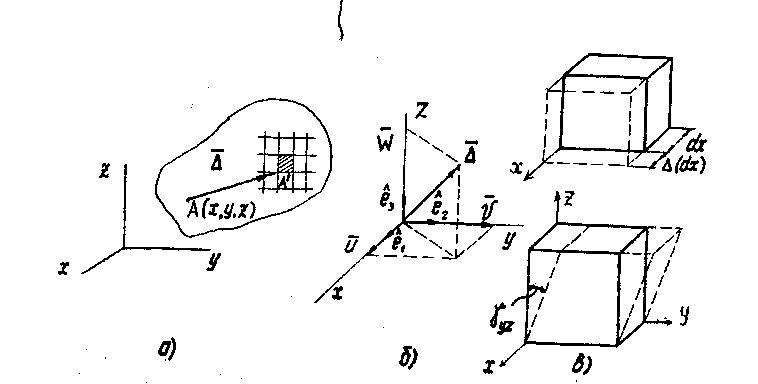
Рис.1.8

Характеристиками ее деформации являются три абсолютных удлинений ее ребер и три изменения угла между ними , называемые сдвигами.

Относительными удлинениями ребер назовем величины

, , .

Три относительных удлинения и три деформации сдвига

называют компонентами деформированного состояния материальной частицы тела.

Глава 2. Растяжение, сжатие бруса

Как уже упоминалось, под растяжением понимается такой вид нагружения бруса, когда в его поперечных сечениях возникают только нормальные силы. Сжатие отличается от растяжения, только знаком силы . При растяжении нормальная сила направлена от сечения, а при сжатии — к сечению. Таким образом, при анализе внутренних сил сохраняется единство подхода к вопросам растяжения, сжатия.

1. Напряжения и деформации при растяжении и сжатии. Закон Гука

Пусть брус растянут силами (рис. 2.1). Площадь поперечного сечения . Нормальная сила в сечении равна (рис. 2.1,б).

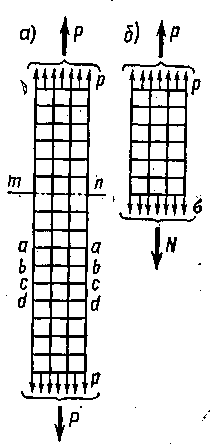
Рис. 2.1

Нормальная сила является равнодействующей всех внутренних сил , действующих на бесконечно малых площадках

. (2.1)

Эксперименты показывают, что если на достаточном удалении от точки приложения сил нанести на поверхность бруса ортогональную сетку, то после деформации она также останется ортогональной, только изменятся расстояния между линиями. Горизонтальные сечения плоские до деформации останутся плоскими после деформации (гипотеза плоских сечений Бернулли). Отсюда естественно предположить, что нормальные напряжения распределяются равномерно по сечению .

Из (2.1) следует

или . (2.2)

Понятно, что высказанное предположение о равномерном распределении внутренних сил в поперечном сечении справедливо лишь постольку, поскольку из рассмотренного исключаются особенности приложения внешних сил (рис. 2.2).

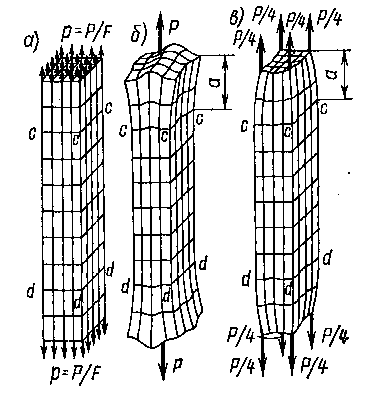
Рис. 2.2

Здесь руководствуются принципом Сен-Венана (французский ученый прошлого века). Особенности приложения внешних сил к растянутому стержню проявляются на расстояниях, не превышающих характерных размеров поперечного сечения стержня. Т.е. при изучении растяжения стержня достаточно принимать во внимание только равнодействующую внешних сил , не интересуясь особенностями приложенной нагрузки.

Приведенные рассуждения могут быть отнесены также и к особым участкам, содержащим резкое изменение геометрии ферм, отверстия и т.п. (рис. 2.3).

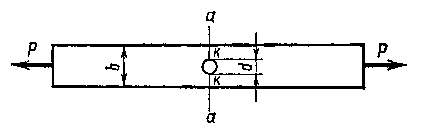
Рис. 2.3

Теперь рассмотрим деформации при растяжении. Под действием внешней нагрузки длина стержня увеличивается, а поперечные сечения уменьшаются (рис. 2.4). Пунктирной линией показан деформированный стержень.

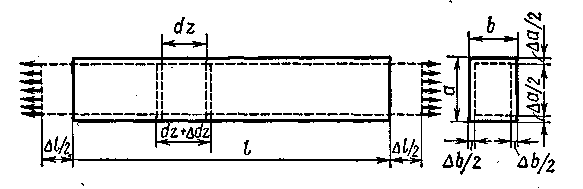
Рис. 2.4

Мысленно вырежем элемент длиною . Продольная линейная деформация этого элемента

; .

Абсолютное увеличение стержня равно ( , )

.

Таким образом, продольная деформация стержня при простом растяжении равна

. (2.3)

Поперечные деформации найдем

Для изотропных материалов

.

Отношение поперечной деформации к продольной, взятое по абсолютной величине, называется коэффициентом Пуассона

. (2.4)

Для всех изотропных материалов

.

Между напряжениями и деформациями существует в пределах упругости зависимость, называемая законом Гука:

(2.5)

Подставляя (2.3) в (2.5) имеем

или , (2.6)

где — жесткость стержня при растяжении.

Для ступенчатого стержня нагруженного несколькими силами формула для определения абсолютной деформации имеет вид:

. (2.7)

Если и изменяется по какому-либо закону, то

,

— нормальная площадь напряженного сечения. (2.8)