
- •Введение
- •Глава 1. Основы сопротивления материалов
- •Предмет «Сопротивление материалов»
- •Объект курса
- •Внешние силы
- •Основные понятия и гипотезы (допущения)
- •Внутренние силы и их определение. Метод сечений
- •Эпюры внутренних усилий
- •Понятие о напряжении и напряженном состоянии
- •Понятие о деформации тела и о деформации физических точек
- •Глава 2. Растяжение, сжатие бруса
- •Напряжения и деформации при растяжении и сжатии. Закон Гука
- •Потенциальная энергия деформации
- •Анализ напряженного состояния при растяжении (сжатии)
- •Статически определимые и статически неопределимые задачи при растяжении и сжатии
- •Диаграмма растяжения
- •2.6. Диаграмма сжатия
- •2.7. Расчеты на прочность при растяжении (сжатии)
- •Глава 3. Сдвиг и кручение стержней
- •3.1. Понятие о чистом сдвиге. Напряжения и деформации при сдвиге. Закон Гука
- •Практический расчет соединений работающих на сдвиг
- •Кручение бруса с круглым поперечным сечением. Напряжение в брусе круглого поперечного сечения. Условия прочности. Определение угла закручивания. Условие прочности
- •Кручение бруса прямоугольного поперечного сечения
- •Потенциальная энергия бруса при кручении
- •Кручение бруса круглого поперечного сечения за пределом упругости
- •Глава 4. Геометрические характеристики плоских сечений
- •Основные понятия
- •Статические моменты сечения
- •Моменты инерции сечения. Зависимость между моментами инерции при параллельном переносе осей
- •Зависимость между моментами инерции сечения при повороте осей. Главные оси и главные моменты инерции
- •Глава 5. Изгиб
- •5.1. Основные понятия
- •5.2. Дифференциальные зависимости между и
- •5.3. Напряжения в брусе при чистом изгибе
- •5.4. Напряжения при поперечном изгибе
- •5.5. Чистый косой изгиб
- •Внецентренное растяжение и сжатие
- •Глава 6. Перемещения при изгибе
- •6.1. Метод Мора для определения перемещений
- •6.2. Способ Верещагина
- •Глава 7. Статически неопределимые стержневые системы
- •7.1. Введение
- •7.2. Классификация стержневых систем. Системы статической неопределимости
- •7.3. Метод сил. Выбор основной системы
- •7.4. Канонические уравнения метода сил
- •7.5. Использование свойств симметрии при раскрытии статической неопределенности
- •7.6. Определение перемещений в статически неопределимых системах
- •Глава 8. Устойчивость равновесия деформируемых систем
- •8.1. Основные понятия
- •8.2. Дифференциальное уравнение стержня потерявшего устойчивость
- •8.3. Задача Эйлера об устойчивости шарнирно опертого стержня сжатого силой р
- •8.4. Зависимость критической силы от условий закрепленного стержня
- •8.5. Пределы применимости формулы Эйлера
- •8.6. Практический метод расчета стержней на устойчивость
- •Глава 9. Элементы теории напряженного и деформированного состояния
- •9.1. Основные понятия
- •9.2. Напряжения на наклонных площадках
- •9.3. Главные оси и главные напряжения
- •9.4. Круговая диаграмма напряженного состояния
- •9.5. Экстремальные касательные напряжения
- •9.6. Октаэдрические площадки. Октаэдрические напряжения
- •9.7. Деформированное состояние
- •9.8. Формулы обобщенного закона Гука
- •Глава 10. Критерии пластичности и разрушения
- •10.1. Постановка вопроса
- •10.2. Условия пластичности и разрушения
- •Гипотеза пластичности Треска—Сен—Венана
- •Гипотеза пластичности Хубера—Мизеса
- •10.3. Теория пластичности и разрушения Мора
- •Глава 11. Прочность материалов при циклически изменяющихся напряжениях
- •11.1. Понятие об усталостной прочности
- •11.2. Виды циклов напряжений
- •11.3. Предел выносливости
- •11.4. Диаграмма предельных амплитуд
- •11.5. Факторы, влияющие на усталостную прочность
- •11.5.1 Концентрация напряжений
- •11.5.2 Масштабный эффект
- •11.5.3 Влияние качества обработки поверхности
- •11.6. Расчет на прочность при переменных напряжениях
8.6. Практический метод расчета стержней на устойчивость
При назначении размеров сжатого стержня в первую очередь необходимо заботится о том, чтобы он в процессе эксплуатации не потерял устойчивость. Поэтому напряжения в стержне должны быть обязательно меньше критических
![]() .
(а)
.
(а)
Здесь
—
сжимающая сила в стержне,
![]() — критическое напряжение,
— критическое напряжение,
![]() —
коэффициент запаса устойчивости,
—
коэффициент запаса устойчивости,
![]() — площадь поперечного сечения брутто
(без учета ослабленного сечения
отверстиями, вырубками и
— площадь поперечного сечения брутто
(без учета ослабленного сечения
отверстиями, вырубками и
т.д. Они мало влияют на величину критической силы).
При расчете растянутых стержней на прочность применяется формула
![]() (б)
(б)
Поделим (а) на (б)
и обозначим отношение правых частей
через
![]()
![]() или
или
![]() ,
,
где — коэффициент уменьшения основного расчетного сопротивления при продольном изгибе. Оно называется “коэффициентом продольного изгиба” и зависит от гибкости стержня.
т.е.
![]() .
.
Расчетная формула для сжатых стержней принимает вид
![]() ,
или
,
или
![]() ,
(8.11)
,
(8.11)
где
![]() берется по таблице.
берется по таблице.
Расчетная формула для сжатого стержня внешне совпадает с расчетной формулой для растянутого стержня. Она удобна тем, что позволяет пользоваться одним допускаемым напряжением, как для растянутого, так и для сжатого стержня.
Глава 9. Элементы теории напряженного и деформированного состояния
9.1. Основные понятия
Совокупность напряжений, возникающих во множестве площадок, проходящих через данную точку, называют напряженным состоянием в точке (или тензором напряжений).
Пусть имеется твердое тело, нагруженное произвольной системой сил (рис. 9.1).
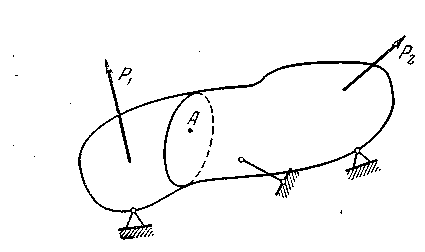
Рис. 9.1
Возьмем произвольную
т.
вырежем простейшую фигуру — прямоугольный
параллелепипед с гранями
.
На гранях будут действовать вектора
полных напряжений
![]() каждый из которых может быть разложен
на три составляющиеся по осям (рис. 9.2).
каждый из которых может быть разложен
на три составляющиеся по осям (рис. 9.2).
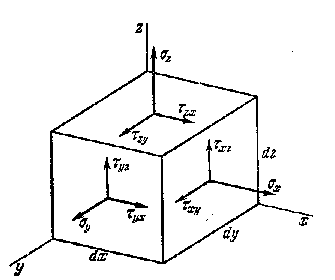
Рис. 9.2
На невидимых гранях действуют такие же напряжения, но противоположно направленные. Этот элемент находится в равновесии, т.к. удовлетворяет уравнение статики
![]()
![]()
Последние три
позволяют получить следующие соотношения
![]() — закон парности касательных напряжений.
— закон парности касательных напряжений.
В силу этого закона из указанных девяти напряжений различны только шесть. Нормальные напряжения считаются положительными, когда они вызывают растяжение элемента. Положительное напряжение компонент касательных напряжений совпадающих с положительным направлением осей, если растягивающие нормальные напряжения для той же грани совпадают с положительным направлением соответствующей оси.
9.2. Напряжения на наклонных площадках
Если даны
шесть составляющих напряжений
![]() на трех взаимно перпендикулярных
площадках, то можно найти напряжение
на любой наклонной площадке, проходящей
через данную точку (рис. 9.3).
на трех взаимно перпендикулярных
площадках, то можно найти напряжение
на любой наклонной площадке, проходящей
через данную точку (рис. 9.3).
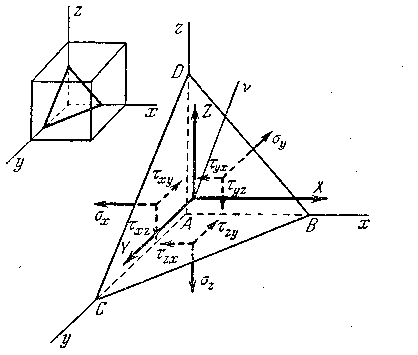
Рис. 9.3
Положение в
пространстве площадки
![]() определяются нормалью
,
направляющие косинусы которой:
определяются нормалью
,
направляющие косинусы которой:
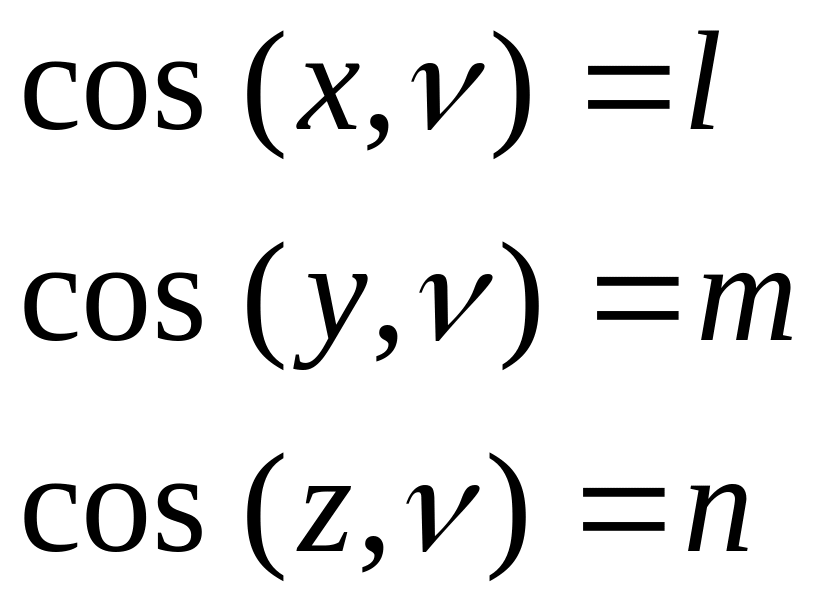
Наклонная площадка
вместе с координатами площадками
![]() образуют бесконечно малый тетраэдр.
Обозначим площадь грани
через
,
тогда площади:
образуют бесконечно малый тетраэдр.
Обозначим площадь грани
через
,
тогда площади:
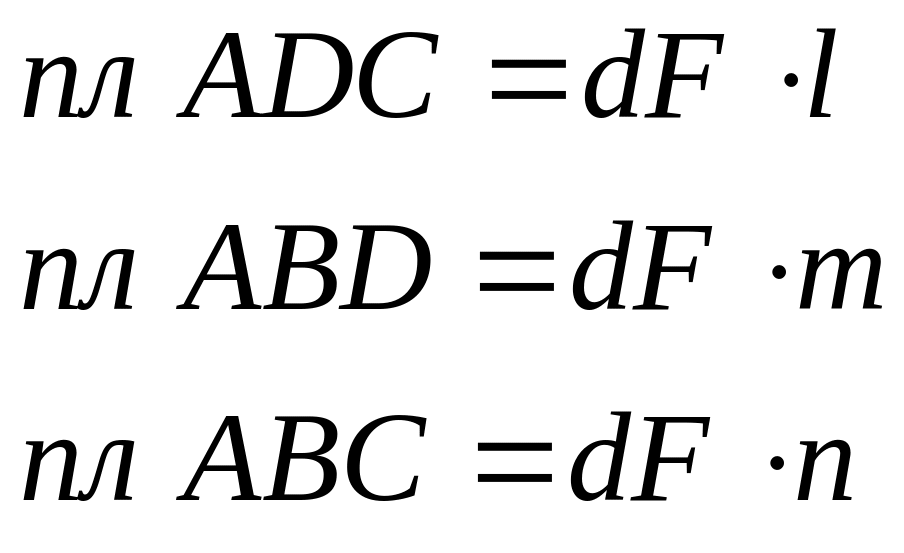
Проектируя все
силы, действующие на тетраэдр на оси
![]() с учетом последнего соотношения, после
сокращения на
получим:
с учетом последнего соотношения, после
сокращения на
получим:
![]() (9.1)
(9.1)
Полученная система носит название формул Коши.
