8.2. Дифференциальное уравнение стержня потерявшего устойчивость

Рассмотрим стержень, защемленный одним концом и шарнирно опертый на другом. Приложим продольную силу . Отклоним его от положения равновесия и рассмотрим равновесие отсеченной части.

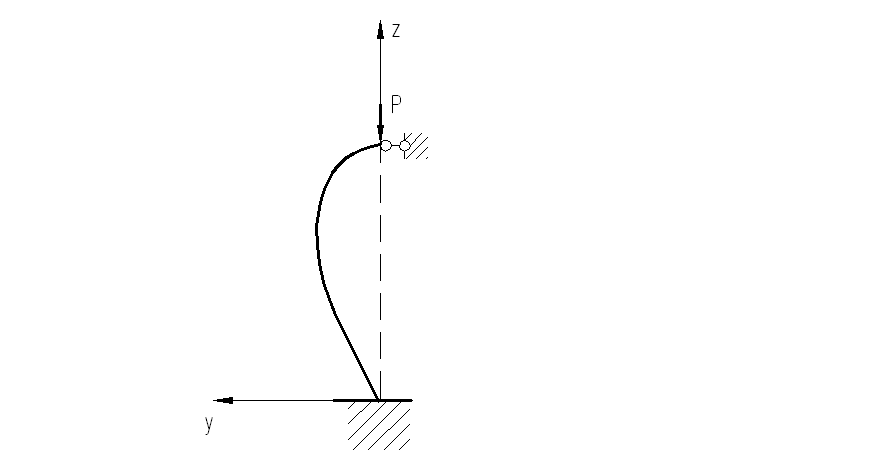
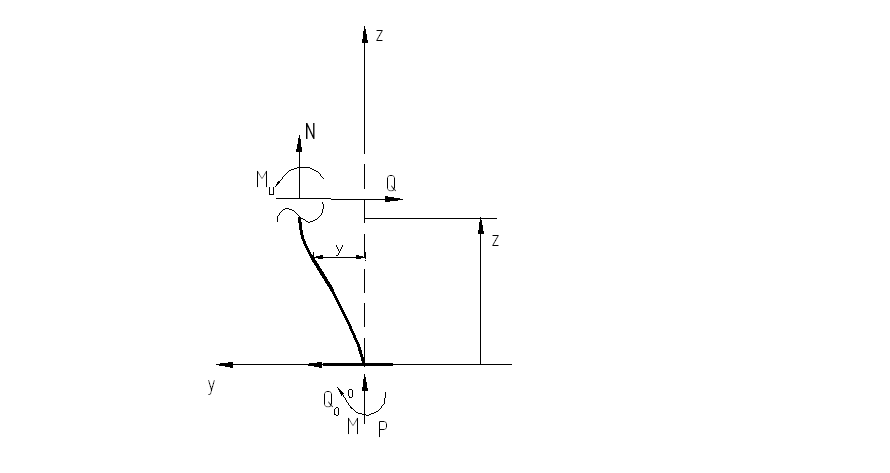
Рис. 8.3

Выпишем дифференциальное уравнение, изогнутой оси стержня.

Изгибающий момент в произвольном сечении , равен

,

где .

.

Получим линейное неоднородное уравнение второго порядка. Продифференцировав его два раза по придем к однородному.

или

, (8.1)

где (8.2)

Общий интеграл уравнения (8.1) имеет вид

(8.3)

8.3. Задача Эйлера об устойчивости шарнирно опертого стержня сжатого силой р

Дифференциальное уравнение (8.1) имеет решения (8.3). Найдем постоянные интегрирования из граничных условий для шарнирно опертого стержня (рис. 8.4).

При или

1). 2).

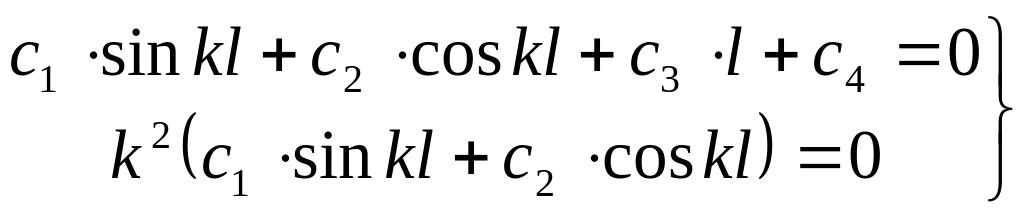
Откуда:

Рис. 8.4

Если , то получим тривиальное решение, т.е. устойчива только прямолинейная форма равновесия.

При , имеем

откуда , где

, но

Тогда получим

, (8.4)

где — число полуволн (рис. 8.5)

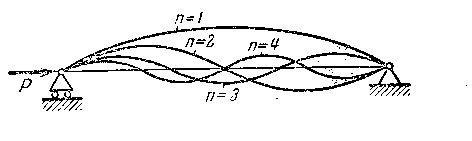
Рис. 8.5

Минимальное значение критической силы будет при . В итоге получим формулу критической силы для шарнирно опертого стержня.

(8.5)

8.4. Зависимость критической силы от условий закрепленного стержня

На рис. 8.6 показаны различные случаи закрепления сжатого стержня. Для каждого случая необходимо проводить решение, как это сделано в предыдущем параграфе. Решение этих задач показало, что всех случаев, изображенных на рисунке, критическую силу можно определять по обобщенной формуле.

, (8.6)

Где — коэффициент приведенной длины, а величина — приведенная длина. Приведенная длина — условная длина шарнира опертого стержня, имеющего такую же критическую нагрузку, как заданный стержень. В отдельных случаях это видно из геометрии.

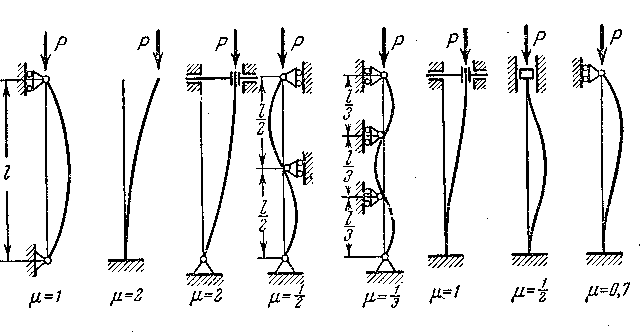
Рис. 8.6

8.5. Пределы применимости формулы Эйлера

Как уже упоминалось, формула Эйлера справедлива при условии, что деформации сжатия вплоть до момента потери устойчивости, подчиняются закону Гука. Иными словами, критическое напряжение не должно превышать предела пропорциональности для данного материала. Найдем выражение для

;

Введем понятие радиуса инерции

, тогда

, (8.7)

Где — гибкость стержня.

Условием применимости формулы Эйлера будет

или (8.8)

Откуда предельная гибкость стержня, при которой еще может использоваться формула Эйлера, будет

(8.9)

Условие (8.8) получает вид (8.10)

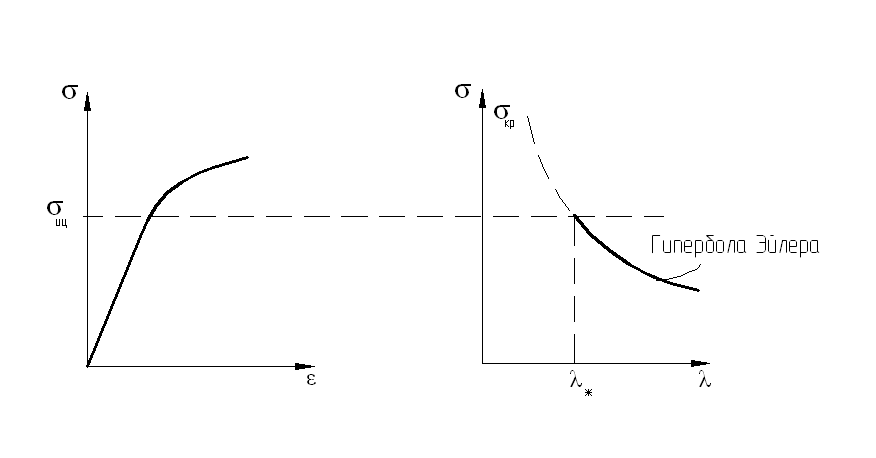
Рис. 8.7

Из этих рисунков видно, что при напряжениях в стержне выше формулой Эйлера для определения пользоваться нельзя.