7.3. Метод сил. Выбор основной системы
Одним из наиболее распространенных методов расчета статически неопределимых систем (С.Н.С.) является метод сил. Он заключается в том, что заданная С.Н.С. освобождается от «лишних» связей, а их действие заменяются неизвестными силами и моментами. Величина их подбирается так, чтобы перемещения в основной (эквивалентной) системе были равны перемещениям в заданной системе. Основной называется статически определимая, геометрически (кинематически) неизменяемая система, полученная из заданной путем отбрасывания лишних связей и заданных нагрузок. Как правило, для одной статически неопределимой системы можно подобрать сколько угодно основных систем.
Рассмотрим
плоскую раму (рис. 7.3). Степень статической
неопределенности «
»
равно
.
Выберем несколько вариантов
основных систем, отбрасывая каждый раз
семь «лишних» связей. Например, для
данной рамы можно предложить основные
системы а), б), ………., которые получены
путем отбрасывания семи связей в
различных комбинациях.
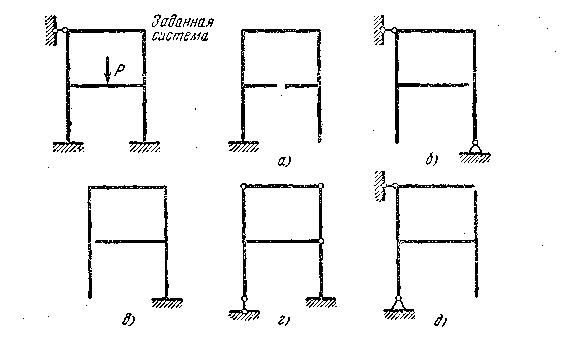
Рис. 7.3
Эквивалентная система — получается из основной, путем загружения неизвестными реакциями отброшенных связей, а также заданной внешней нагрузкой (рис. 7.4).
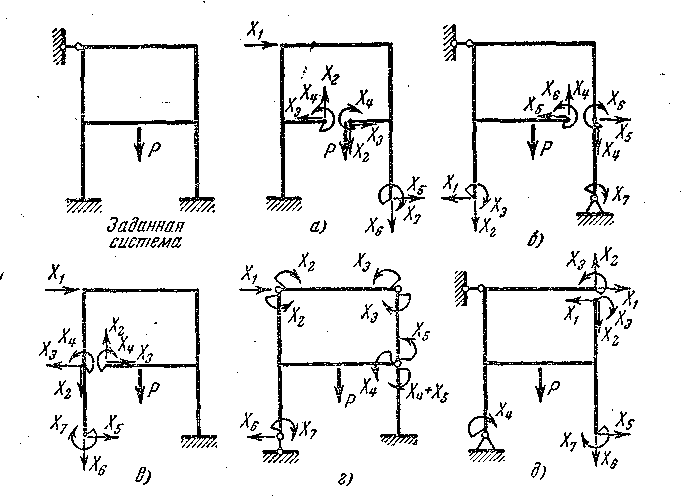
Рис. 7.4
Там, где запрещены линейные перемещения, приложены силы, где угловые — моменты, где взаимные — взаимные моменты и силы.
Теперь
остается составить уравнения для
определения неизвестных
.
7.4. Канонические уравнения метода сил
Обратимся к ранее рассмотренному примеру (рис. 7.5)
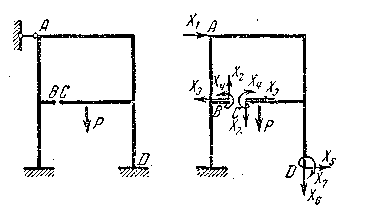
Рис. 7.5
В эквивалентной
системе, также как в заданной, перемещения
по направлению отброшенных связей
должны равняться нулю. На основании
принципа независимости действия сил
перемещения по
— тому направлению от всех сил можно
представить в виде:
(7.1)
Здесь первые
индексы означают направления перемещения
(и одновременно направление отбрасываемой
связи), а вторые — причину вызвавшую
эти перемещения. Таким образом
— означает перемещение по направлению
от
— го силового фактора. Обозначим через
реакцию связи
,
тогда поскольку перемещение пропорционально
соответствующей силе, то
,
(7.2)
где
— единичное перемещение по
—
тому направлению от силы
.
Подставляя (7.2) в (7.1), получим
.
(7.3)
Таким образом,
условие эквивалентности основной и
заданной
статически неопределимой системы
сводится к системе
линейных алгебраических уравнений.
(7.4)
Уравнения (7.4) являются каноническими уравнениями метода сил. Они позволяют раскрыть статические нагрузки системы. Первое из (7.4) означает, что перемещения по первому направлению от всех сил равно нулю и т.д. Число уравнений системы равно степени статической неопределимости.
Единичный
коэффициент
определяется с помощью интегралов Мора,
причем на основании теоремы взаимности
перемещений
.
(7.5)
Грузовой коэффициент
(7.6)
Если с.н.с. состоит из прямолинейных участков, то интегралы Мора (4.2), (4.3) можно вычислять по правилу Верещагина.
Вернемся теперь
к математическим свойствам системы
(4.1). Коэффициенты
называются главными, они всегда
положительные. Побочные коэффициенты
—
,
могут быть положительными и отрицательными.
— свободные члены уравнений или грузовые
коэффициенты. Могут быть положительными
и отрицательными.
Напомним еще раз, что в балках и рамах в подавляющем большинстве случаев перемещения от изгиба и кручения намного больше перемещений от растяжения и сдвига. Поэтому в (7.5) и (7.6) последними тремя интегралами, как правило, можно пренебречь.