Глава 6. Перемещения при изгибе

6.1. Метод Мора для определения перемещений

Если материальная точка находится в равновесии под действием некоторой системы сил (рис. 6.1), то сумма работ этих сил на любом возможном перемещении равна нулю.

. (6.1)

Рис. 6.1

Любое упругое тело можно рассматривать как систему материальных точек, находящихся в равновесии под действием внешних и внутренних сил упругости. Следовательно, работа всех внешних и внутренних сил упругости на любом возможном перемещении для упругого тела равна нулю.

Пусть под воздействием внешних сил в балке возникли действительные перемещения , и под действием внешних и внутренних сил упругости оно находится в равновесии (рис. 6.2,а). Назовем его действительным состоянием (I состояние). Представим себе II состояние (фиктивное), в котором все силы есть вариации сил действительного состояния, тогда и перемещения в нем будут вариациями перемещений первого состояния (рис. 6.2,б). Составим работу сил первого состояния на перемещениях второго.

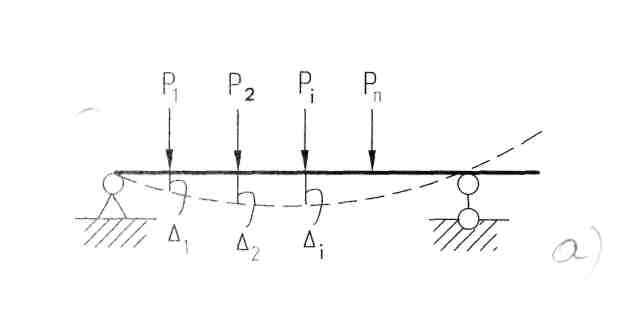
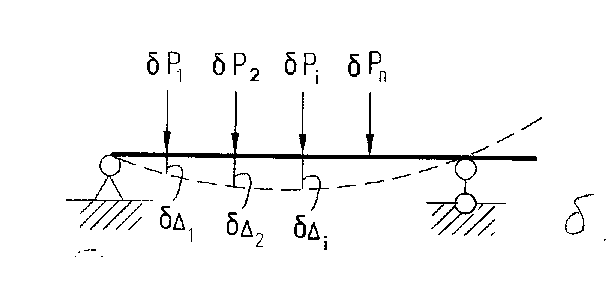
Рис. 6.2

, (6.2)

где — работа внутренних сил. Тогда можно записать

. (6.3)

Возьмем теперь два состояния упругой системы (рис. 6.3).

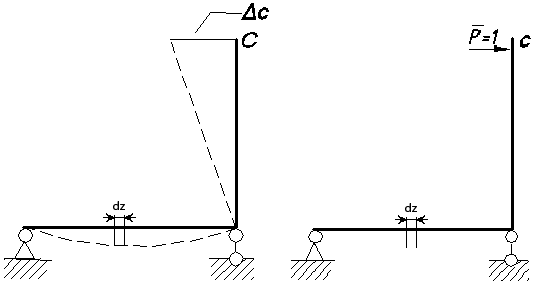
Рис. 6.3

Рассматривая перемещения точек состояния I (рис. 6.3,а) как возможные, составим на основании принципа Лагранжа работу II — состояния (рис. 6.3,б) на перемещениях I.

, ( — связана со статическим приложением силы)

или . (6.4)

Вычислим работу внутренних силовых факторов второго состояния на перемещениях первого. Для этого из I и II состояний вырежем участок бруса длиной (рис. 6.3).

Элементарная работа внутренних сил II состояния на перемещениях I, равна:

.

Деформации малого элемента определяются по известным формулам.

При растяжении: .

При изгибе, кручении: , , .

При сдвиге: .

Абсолютный сдвиг: ; ; ; .

Т.к. касательные силы распределены по сечениям неравномерно то , где — поправочный коэффициент, учитывающий неравномерное распределение касательных напряжений (рис. 6.4).

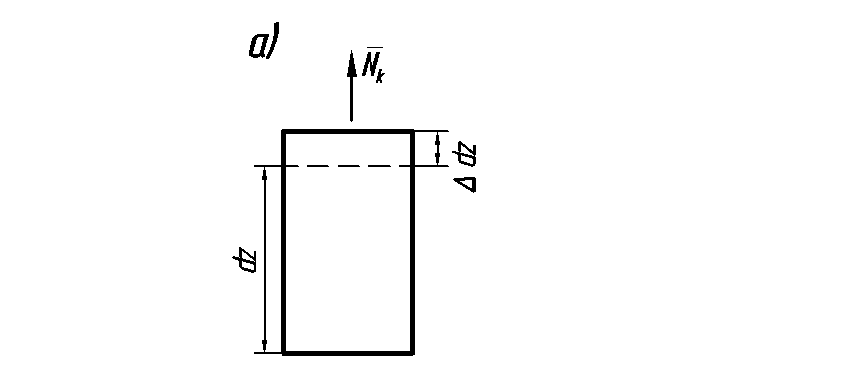
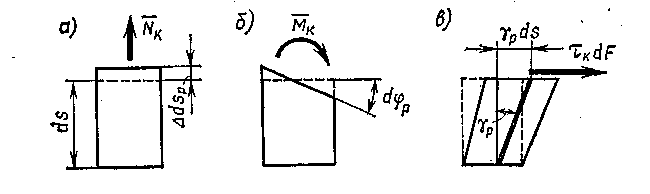
Рис. 6.4

Подставляя перемещения в выражения для , получим:

Для всей системы

Подставляя в уравнение Лагранжа (6.3), получим

(6.5)

В правой части этого выражения стоят интегралы Мора.

Если определяются перемещения в пространственных системах, то первыми тремя интегралами пренебрегают.

(6.6)

Если определять перемещения в плоских балках, рамах, то

(6.7)

Если определять перемещения в фермах, то

(6.8)