5.5. Чистый косой изгиб

Изгиб называется косым, если плоскость действующих сил проходит через ось балки, но не совпадает ни с одной из главных осей сечения.

Его удобнее всего рассматривать как одновременный изгиб бруса в двух главных плоскостях и (рис. 5.13).

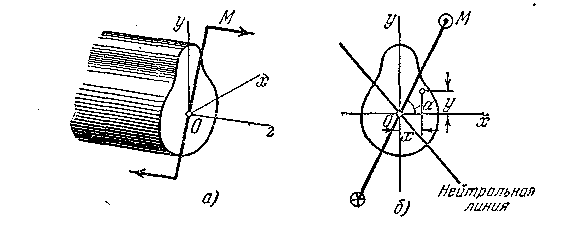
Рис. 5.13

Для этого изгибающий момент раскладывается на составляющие относительно осей и :

, .

Таким образом, косой изгиб сводится к двум плоским изгибам относительно осей, и . Изгибающие моменты считаются положительными, если они вызывают растяжение в первой четверти.

Нормальные напряжения в точке имеющей координаты и будут равны сумме напряжений от , т.е.

(5.13)

Следовательно, как при простом изгибе нормальные напряжения при косом изгибе образуют плоскость.

Уравнение нейтральной линии получим, положив в (5.13) .

.

После подстановки и получим

, т.к. , то или окончательно уравнение нейтральной линии получим в виде:

. (5.14)

Легко установить, что при косом изгибе нейтральная линия не перпендикулярна плоскости изгибающего момента.

Угловой коэффициент следа плоскости момента (рис. 5.13,б) представляет собой тангенс угла ,

.

Угловой коэффициент нейтральной линии равен

.

Т.к. в общем случае , то условие перпендикулярности прямых, известное из аналитической геометрии, не соблюдается, поскольку

.

Поэтому нейтральная линия не перпендикулярна к плоскости момента, а несколько повернута в сторону минимального момента инерции. Брус «предпочитает» изгиб не в плоскости изгибающего момента, а в некоторой другой плоскости, где плоскость на изгиб будет меньше.

Т.к. эпюра нормальных напряжений в сечении линейка, то максимальные напряжения возникают в точке, наиболее удаленной от нейтральной линии. Пусть координаты этой точки будут тогда:

. (5.15)

Условие прочности можно записать в виде:

. (5.16)

Если сечение имеет простую форму, то наиболее удаленные точки находятся сразу, если сложную то, вычертив сечение в масштабе (рис. 5.14), наносится положение нейтральной линии, и графически находится наиболее удаленная точка (рис. 5.14).

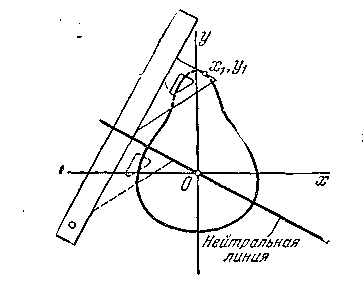
Рис. 5.14

6. Внецентренное растяжение и сжатие

При внецентренном растяжении равнодействующая внешних сил не совпадает с осью бруса, как при растяжении и смещена относительно оси и параллельна ей.

Пусть в точке приложена равнодействующая сила равная . Координаты ее и . От этой силы в произвольном сечении стержня возникает нормальная сила и два изгибающих момента и (рис. 5.15).

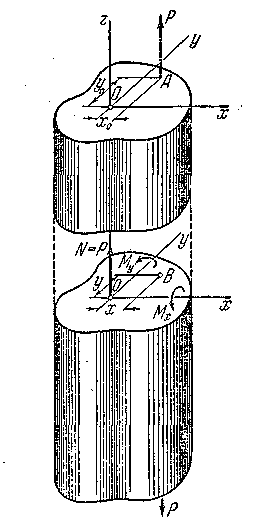
Рис. 5.15

Причем .

Правило знаков: нормальную силу считают положительной, если она вызывает растяжение. Изгибающие моменты и считают положительными, если они вызывают растяжение в первой четверти.

Возьмем произвольную точку с координатами и . Нормальные напряжения в этой точке определяем по формуле

(5.17)

Пространственная эпюра напряжений образует плоскость. Так как эпюра напряжений образует плоскость, то положение нулевой линии определится как линия пересечения этой плоскости с плоскостью поперечного сечения. Уравнение нейтральной линии получаем, приравнивая нулю:

(5.18)

Расчет на прочность ведется для наиболее удаленной точки .

(5.19)

Эта линия не проходит через начало координат, как в случае косого изгиба. Проведем нейтральную линию, определив отрезки, отсекаемые ею на осях. Обозначим отрезки на осях отсекаемые нейтральной линией (рис.5.16,а).

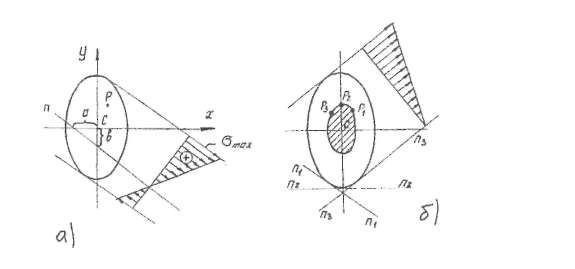
Рис. 5.16

При , — отрезок отсекаемой нулевой линии на оси . При , — отрезок отсекаемой нулевой линии на оси . Заменим , тогда .

Введем понятие радиуса инерции

(см), (см)

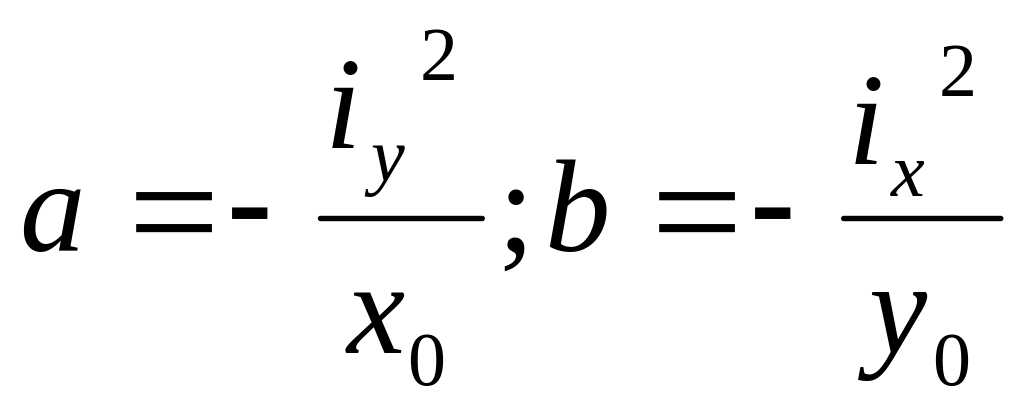. Если , то .

Если точка приложения силы приближается к центру, то нулевая линия будет уходить в бесконечность и наоборот. Если нейтральная линия пересекает поперечное сечение (рис. 5.16,а), то в частях, расположенных по разные стороны от нее, нормальные напряжения (5.16) имеют разные знаки. Пусть нейтральная линия касается контура поперечного сечения (положение ). Соответствующая точка приложения силы находится в полюсе . Если теперь катить нейтральную линию по контуру сечения (положение и т.д.), то полюс будет описывать вокруг центра тяжести сечения некоторую замкнутую кривую (рис. 5.16,б), область внутри которой называется ядром сечения. Если сила приложения внутри ядра сечения, то нейтральная линия находится вне сечения и в нем возникают напряжения одного знака.