4.4 Определение допускаемых напряжений изгиба в зацеплении зубчатых передач.

4.4.1. Эквивалентное число циклов нагружения деталей за срок службы.

для шестерни и колеса:

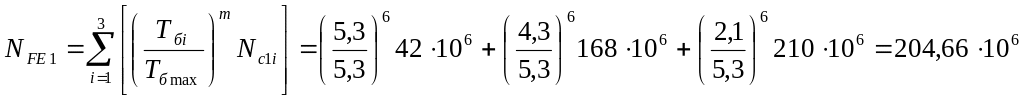
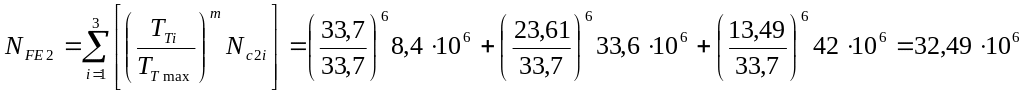
где m=6 - показатель степени при Н≤350НВ

Так как N_FE  4 ·10⁶, то принимаем N_FE = 4 ·10⁶.

4.4.2. Базовое число циклов перемены напряжений.

Для зубчатой передачи N_FO = 4 ·10⁶.

4.4.3. Коэффициент долговечности при действии изгибных напряжений.

для шестерни и колеса:

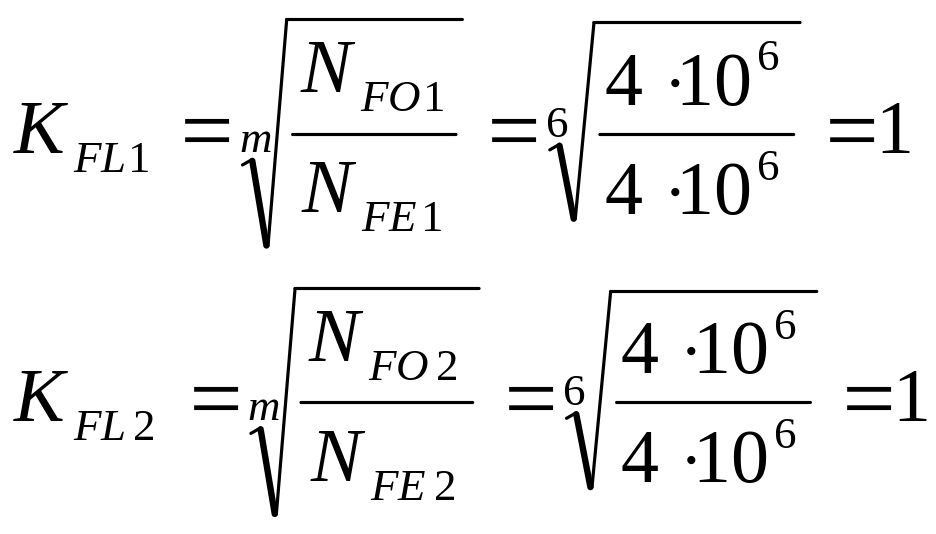
при Н≤350НВ - 1 ≤К_{FL i}≤2,08;

4.4.4. Допускаемые изгибные напряжения, соответствующие пределу выносливости [σ]_FO и рабочему режиму передачи [σ]_Fi .

Таблица 4.4.4.1. Допускаемые изгибные напряжения.

Передача	Параметр	Н≤350НВ
коническая	[σ]FO1 [σ]FO2	1,03  НВср= 1,03  285,5 = 294,065 1,03  НВср= 1,03  248,5 = 255,955
	[σ]Fi1 [σ]Fi2	КFL  [σ]FO= 1  294,05 = 294,05 КFL  [σ]FO= 1  255,95 = 255,955
	[σ]Fрас	min{[σ]Fi2}= 255,955
	Так как передача работает в реверсивном режиме, то полученное значение допускаемого напряжения [σ]Fрас уменьшаем на 25%: [σ]Fрас1 = 0,75  294,065 = 220,55 [σ]Fрас2 = 0,75  255,955 = 191,97

Использование данной методики расчетов позволяет учитывать переменность нагрузки соответствующим выбором допускаемых напряжений. Введение эквивалентных значений циклов перемены напряжений заменяет переменную нагрузку постоянной, но детали приобретают ту же степень усталостных повреждений. Это упрощает проектировочные расчеты на последующих стадиях разработки механических передач.

Таблица 4.4.4.2. Сводная таблица механических характеристик передачи.

Передача	Элемент передачи	Марка материала	Dпред	Термообработка	HBср	σ-1	σв	σт	[σ]Hрас	[σ]Fрас
			Sпред			Н/мм2
Коническая	Шестерня	40Х	125 125	У	285,5	410	900	750	514,3	220,55
	Колесо	40X			248,5	375	790	640		191,97

5. Расчет прямозубой конической передачи

5.1. Проектный расчет

5.1.1. Исходные данные для расчета:

крутящий момент на выходном колесе Т₂ = 34,1 Нм;

частота вращения шестерни n₁ = 700 об/мин;

частота вращения колеса n₂ = 140 об/мин;

передаточное число передачи u_зп = n₁ / n₂ = 700 / 140 = 5

Основной габаритной характеристикой конической зубчатой передачи является средний делительный диаметр выходного колеса d_m2, ориентировочную величину которого определяем по формуле:

d_m2 = K_зк  M  (T₂)^1/3  K_k = 228.65 мм

где K_зк = 1 – коэффициент для передач с прямыми зубьями;

M = (600 / σ_HP)^2/3 = (600 / 463)^2/3 = 1,108 – параметр, уточняющий прочностную характеристику материала

где σ_HP = 463 МПа – допускаемое контактное напряжение на рабочих поверхностях зубьев;

K_k = 47,98 – коэффициент, назначаемый в зависимости от коэффициента ширины колеса K_Be (Принимаем K_Be = 0,2.).

5.1.2. Определение характеристик и размеров шестерни и колеса.

Назначаем числа зубьев шестерни и колеса:

z₁ = 17;

z₂ = 17  u_зп = 85.

Находим ориентировочное значение среднего ок­ружного модуля:

m^’_nm = d^’_m2 / z₂ =255/85=3 мм

округляем его до стандартного значения m_nm = 3 мм.

Корректируем значение среднего делительного диаметра колеса и определяем средний делительный диаметр шестерни:

d_m2 = m_nm  z₂ = 255 мм

d_m1 = m_nm  z₁ =51 мм

Углы делительных конусов:

δ^’₂ = arctg u_зп = arctg 5 = 78.40;

δ^’₁ = 90° – 78.40° = 11.20°;

Внешний окружной модуль:

m_te = m_nm /(1 - 0,5  K_Be) = 3 мм;

Внешние делительные диаметры:

d_e1 = d_m1 /(1 - 0,5  K_Be) = 33.56 мм;

d_e2 = d_m2 /(1 - 0,5  K_Be) =255 мм

Внешнее конусное расстояние:

R_e = 0,5  m_te  (z₁² + z₂²)^1/2 = 143,03мм;

Ширина зубчатого венца:

b₂ = К_ве R_e ≤ 10 d_e1 / z₁= 30 мм

Принимаем b₂ = 17 мм

Среднее конусное расстояние:

R_m = R_e – 0,5  b₂ = 128,03 мм;

Коэффициенты среднего нормального смещения:

x_n1 = 2  (1- u_зп ^-2)(1/ z₁)^1/2 = 0,36;

x_n2 = - x_n1 = -0,36;

Высоты ножек зубьев в среднем сечении:

h_fm1 = (1,25 - x_n1)  m_nm = (1,25 – 0,36)  1,5 = 1,1 мм;

h_fm2 = (1,25 - x_n2)  m_nm = (1,25 + 0,36)  1,5 = 2,3 мм;

Внешние диаметры:

d_ae1 = d_e1 + 1,64  (1+ x_n1)  m_te  cos δ^’₁° = 51 мм;

d_ae2 = d_e2 + 1,64  (1 + x_n2)  m_te cos δ^’₂° = 255мм.

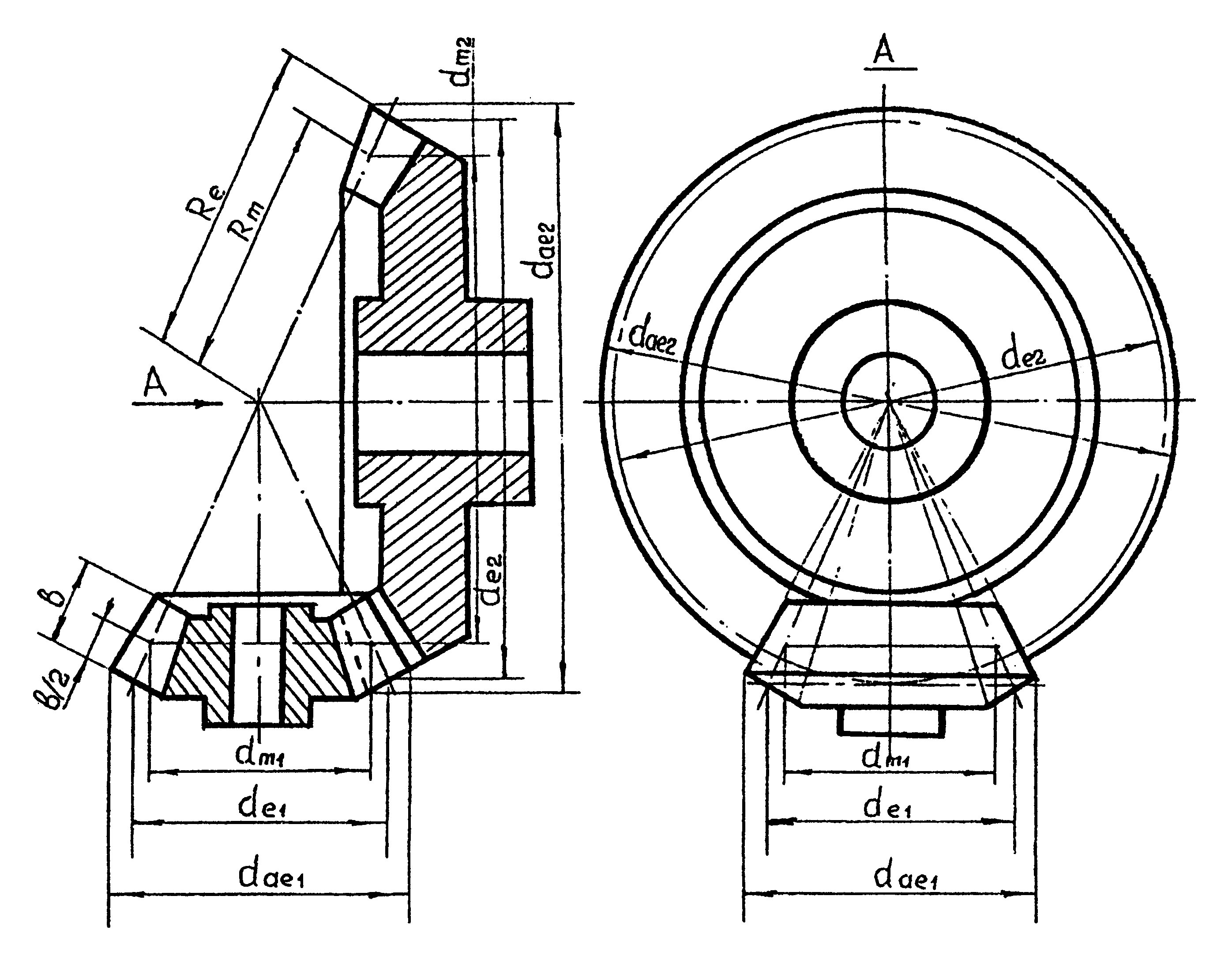
Рисунок 5.1.2.1. Зацепление зубчатого конического колеса и шестерни.