Некоторые тензорные операции.

При помощи ко- и контравариантных векторов, используя их обобщенные произведения, мы можем получить объекты любого порядка и строения. Такие объекты иногда называют мультипликативными. Вводя в рассмотрение объекты, закон преобразования которых совпадает с законом преобразования обобщенных произведений, мы получим три типа преобразований:

Контравариантные ковариантные

Смешанные

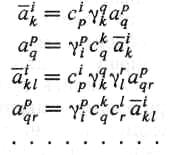
Любой объект, преобразующийся по одному из этих законов, называется тензором или истинным тензором соответствующего порядка и строения.

Важно отметить, что тензорные законы преобразования линейны и однородны. Поэтому, если тензор равен тождественно нулю в какой-нибудь одной системе координат, то он равен тождественно нулю и во всякой другой системе координат.

Для дальнейшего важно установить, что симметрия тензора есть свойство инвариантное, т. е. если имеет место, например, равенство

то отсюда следует, что будет также

Это доказывается следующим образом:

Метрический тензор. Ассоциированные тензоры.

Докажем, что объект, который был назван метрическим тензором, есть дейст­вительно ковариантный истинный тензор.

Объект dr⁽²⁾ есть, очевидно, истинный скаляр. Поэтому мы можем написать

,

а так как , то

откуда, в силу симметрии объекта g_pq, получим

Это — закон преобразования дважды ковариантного истинного тензора, и наше предложение доказано.

Ранее мы условились, что объекты, ассоциированные относительно фундаментального объекта, мы обозначаем одной и той же главной буквой при помощи расположения значков сверху и снизу. Однако теперь мы условились при помощи верхних значков определять контравариантные тензоры, а при помощи нижних — ковариантные. Ассоциированность тензоров и их закон преобразования — это разные вещи. Поэтому необходимо показать, что эти два .различных смысла одних и тех же обозначений не противоречат друг другу, если, в частности, в качестве фундаментального объекта выбран метрический тензор g_pq. Для этого

нужно показать, что объект g_pqa ^q преобразуется как ковариантный вектор а_p, т. е. по закону

Это почти очевидно. В самом деле, мы имеем

Поэтому

Нетрудно показать, что символы Кронекера являются истинными тензорами.

Тензор g^pq . Из элементов метрического тензора по правилам построения обратной матрицы можно получить новый объект, который мы ранее обозначили через g^pq. Докажем, что объект g^pq есть дважды контравариантный истинный тензор.

Чтобы построить матрицу, обратную ||g_pq||, нужно взять алгебраические дополнения элементов g_pq и разделить на детерминант g. По формулам для алгебраических дополнений

Выражение в скобках есть, очевидно, дважды контравариантный псевдотензор веса +2, а в знаменателе стоит псевдоскаляр веса +2. Поэтому g^pq есть истинный тензор.

Как и ранее для ортогональных тензоров, назовем тензорными такие операции, которые, будучи применены к тензорам, приводят к новым тензорам.

Сложение, определенное для однотипных объектов, есть тензорная операция.

Поднимание и опускание индексов есть тензорная операция, потому что, по доказанному, при ее помощи получаются ассоциированные тензоры.

Транспонирование есть тензорная операция. Например, пусть а ^рq есть тензор, тогда

Воспользовавшись правом обозначать немые индексы как угодно получим

откуда видно, что a ^qp есть тоже тензор.

Точно также, если есть тензор, то — тоже тензор, а так как мы условились, что верхний индекс всегда означает номер строки, то и . — транспонированы; следовательно, транспонирование есть тензорная операция.

Отсюда следует, что симметрирование и альтернирование, тоже тензорные операции. Поэтому разложение тензора на симметричную и антисимметричную часть инвариантно, т. е. сохраняется при преобразованиях координат.

Обобщенное произведение тензоров. Закон тензорного преобразования был установлен нами как закон преобразования обобщенного произведения векторов. Поэтому обобщенное умножение тензоров есть тензорная операция.

Свертка. Покажем, что свертка в смысле Эйнштейна, т. е. по одному верхнему и одному нижнему индексам, есть тензорная операция.

Свернем это равенство, положив i = k. Получим

Пусть есть тензор ; его закон преобразования

т. е. в результате свертки получается истинный скаляр. Подобным же образом для тензора третьего порядка имеем

т. е. в результате получаем истинный вектор. Отметим, что при свертке порядок тензора уменьшается на две единицы, одну ковариантную и одну контравариантную.

Наоборот, свертка тензоров по одним верхним или одним нижним индексам не есть тензорная операция. Например, для тензора а ^рq закон преобразования есть

Свернув это равенство по индексам i и k, получим

Следовательно, , т. е. результат свертки не является скаляром.

Скалярное умножение. В предыдущем параграфе мы определили скалярное произведение, как свертку обобщенного произведения двух векторов, взятую в смысле Эйнштейна; например,

Так как свертка в смысле Эйнштейна есть тензорная операция, то скалярное умножение также есть тензорная операция. Скалярное произведение двух истинных векторов есть истинный скаляр.

Векторное умножение. Векторное умножение определено следу­ющим образом:

Мы видим, что в правых частях стоят обобщенные произведения тензоров со сверткой по Эйнштейну. Следовательно, векторное умножение есть тензорная операция.

Смешанное произведение трех векторов. По определению имеем

Здесь в правых частях стоят обобщенные произведения четырех тензоров со сверткой по Эйнштейну. Следовательно, смешанное умножение трех векторов есть тензорная операция, а его результат — истинный скаляр.

8