Задачи и примеры их решения

З адача 5.1. Закрытый резервуар, заполненный жидкостью с плотностью ρ , снабжен ртутным манометром и мановакууметром M (рис. 5.1). Определить показание мановакууметра М, если глубина подключения ртутного манометра H, разность уровней ртути h и расстояние от места подключения манометра до уровня ртути в левом колесе a. Плотность ртути ρ = 13340 кг/м .

Р

А

ис. 5.1

Значения ρ и H принять по предпоследней цифре шифра из табл. 5.1.

Таблица 5.1

Предпо- следняя цифра шифра	0	1	2	3	4	5	6	7	8	9
ρ , кг/м	883	842	854	862	700	722	784	763	684	921
H , м	1,2	1,4	1,6	1,8	2,0	2,2	2,4	2,6	2,8	3,0

Значения h и a принять по последней цифре шифра из табл. 5.2.

Таблица 5.2

Послед- няя цифра шифра	0	1	2	3	4	5	6	7	8	9
h·10, м	150	162	170	180	192	204	215	226	230	249
а, м	0,50	0,55	0,60	0,65	0,70	0,75	0,45	0,40	0,35	0,25

Пример решения задачи

Так как мановакуумметр может измерять избыточное или вакуумметрическое давление, то для определения показания мановакуумметра необходимо определить абсолютное давление над свободной поверхностью жидкости в резервуаре P и сравнить его с величиной атмосферного давления P_am. Если P > P_am, то манометрическое (избыточное) давление

P = P - P_am , (5.1)

Если P < P_am , то вакуумметрическое давление

P = P_am - P . (5.2)

Абсолютное давление над свободной поверхностью жидкости в резервуаре найдём из условия равновесия системы, которое относительно плоскости 1-1, проходящей через границу раздела жидкости и ртути, запишется так:

P +ρ_ж·g·(H+a) = P_am +ρ_pm·g·h (в левой части – давление на точку А сверху, в правой – давление на точку А снизу):

P = P_am +ρ_pm·g·h -ρ_ж·g·(H+a), (5.3)

P =9,81·10 +13340·9,81·0,170-862·9,81·(1,8+0,60)=10,0·10 Па

Сравнивая P c P_am, находим, что P > P_am , следовательно, в резервуаре избыточное давление, а показание мановакуумметра

P = P -P = (10,0-9,81)·10 =1952,2 Па

Задача 2. Определить расход воды Q в горизонтальной трубе диаметром d , имеющей плавное сужение до диаметра d , (расходомер Вентури), если показания пьезометров до сужения h , в сужении h (рис.5.2). Коэффициент, учитывающий уменьшение расхода вследствие потерь напора, μ=0,98.

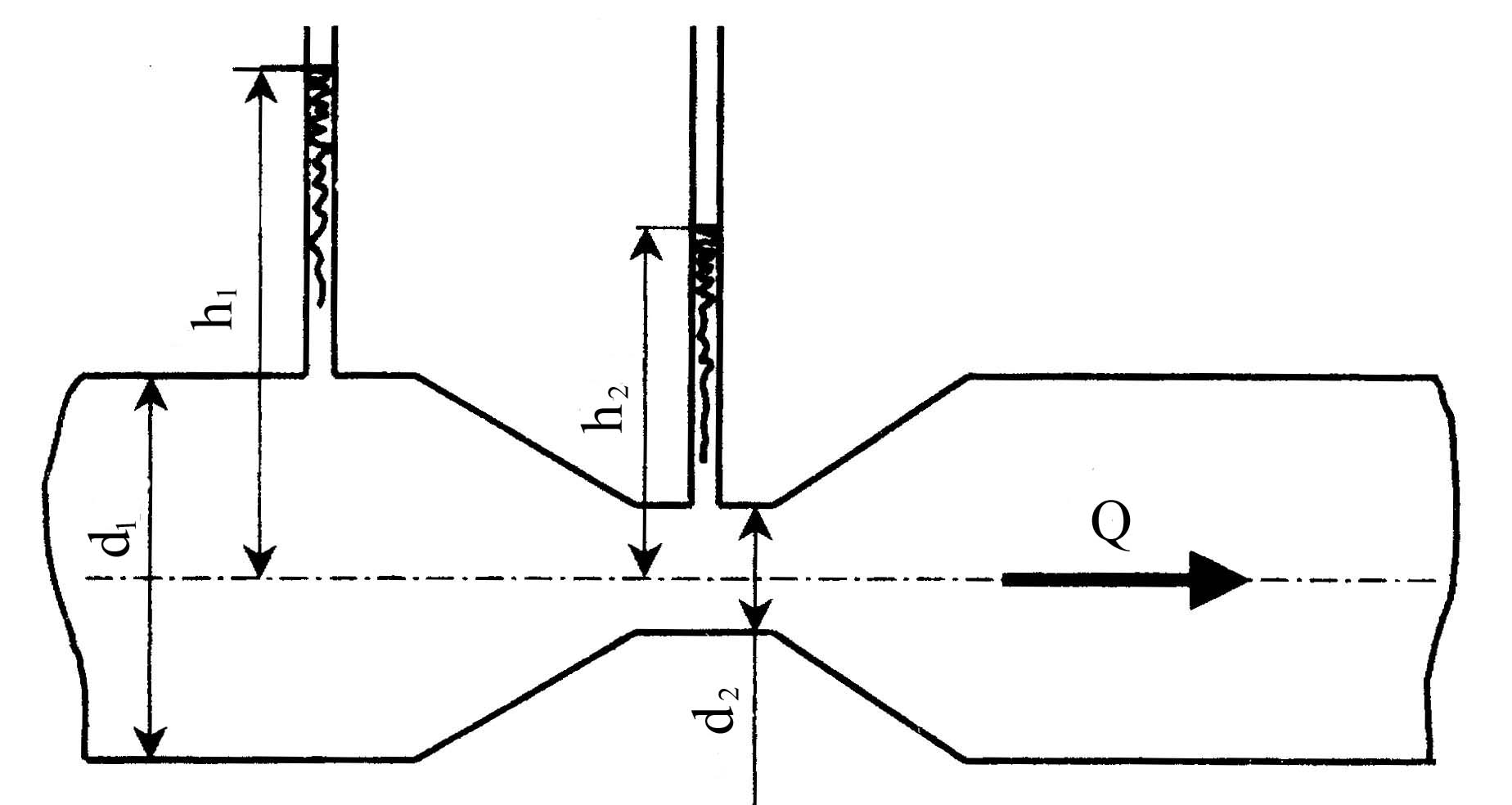
Рис. 5.2

Значения d и d принять по предпоследней цифре шифра из табл. 5.3.

Таблица 5.3

Пред- последняя цифра шифра	0	1	2	3	4	5	6	7	8	9
d ·103,м	250	240	245	255	260	265	270	275	280	285
d ·103,м	125	130	135	140	145	150	120	115	110	105

Значения h и h принять по последней цифре шифра из табл. 5.4.

Таблица 5.4

Последняя цифра шифра	0	1	2	3	4	5	6	7	8	9
h ·102,м	50	51	52	53	54	55	56	57	58	59
h ·102,м	30	32	33	34	35	36	37	38	39	40

Пример решения задачи

Проведем сечения 1 – 1 и 2 – 2 через точки подключения пьезометров h₁ и h₂ соответственно. За плоскость сравнения 0 – 0 выберем ось трубы. Составим и запишем уравнение Бернулли для выбранных сечений, пренебрегая незначительными потерями напора между этими сечениями:

. (5.4)

Так как , , а Z = Z = 0 (трубопровод горизонтален и плоскость сравнения проходит по оси трубопровода), то

или . (5.5)

Скорости и неизвестны, воспользуемся уравнением постоянства расхода

,

где - площади выбранных сечений.

Выразим одну скорость через другую, тогда из уравнения (5.5)

м/с

м³/с.

C учётом потерь расход жидкости

м³/с.

Задача 3. По трубе постоянного сечения из открытого резервуара (рис.5.3) вода вытекает в атмосферу под постоянным напором H. На середине трубы длиной L и диаметром d установлен кран K. Определить скорость и расход вытекающей воды. Построить напорную и пьезометрическую линии. При определении потерь принять коэффициенты трения λ=0,04; входа ζ =0,5; крана ζ =5.

Значения H принять по предпоследней цифре шифра из табл. 5.5.

Таблица 5.5

Предпоследняя цифра шифра	0	1	2	3	4	5	6	7	8	9
H, м	5,0	5,5	6,0	6,5	7,0	7,5	8,0	7,5	7,0	6,5

Рис. 5.3

Значения L и d принять по последней цифре шифра из табл. 5.6.

Таблица 5.6

Последняя цифра шифра	0	1	2	3	4	5	6	7	8	9
L, м	20	25	30	35	40	45	50	55	60	65
d·10-3,м	20	25	40	50	40	25	20	25	40	50