1.1.10. Рівномірна неперервність фбз
Нагадаємо,
що неперервність функції
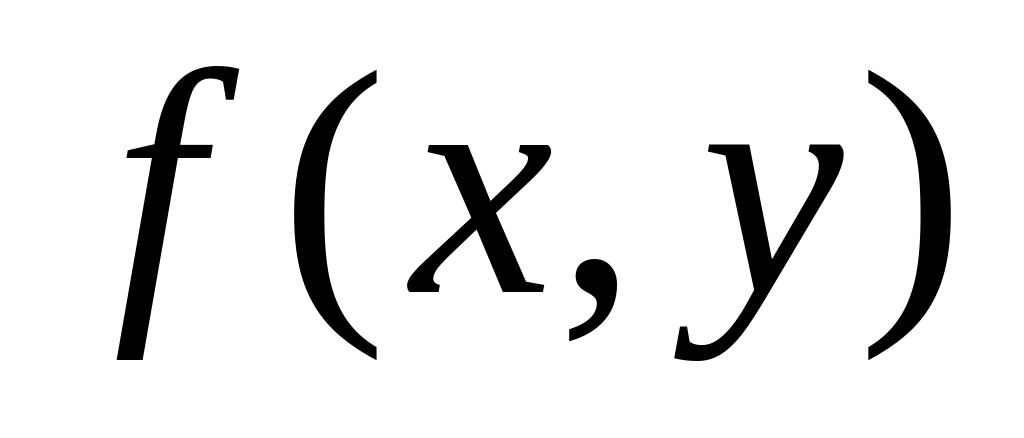 у певній точці
у певній точці
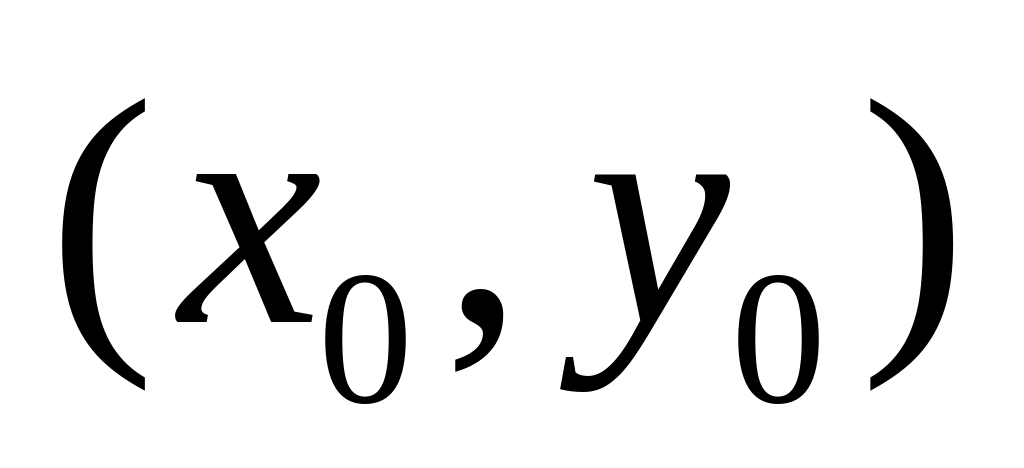 множини М,
де функцію задано, ми сформулювали так:
для будь-якого
множини М,
де функцію задано, ми сформулювали так:
для будь-якого
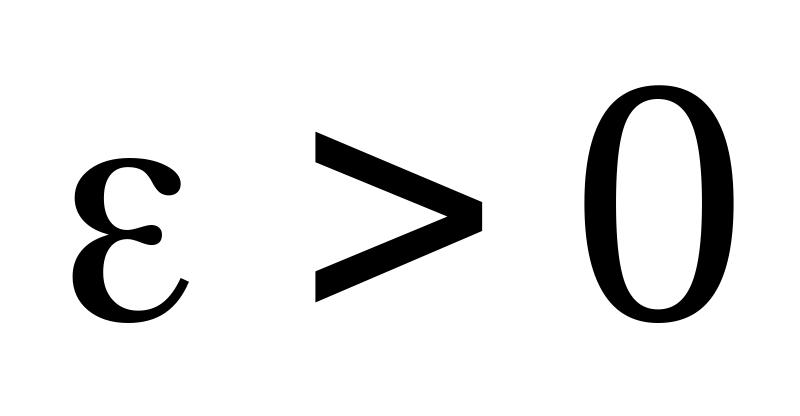 має існувати таке
має існувати таке
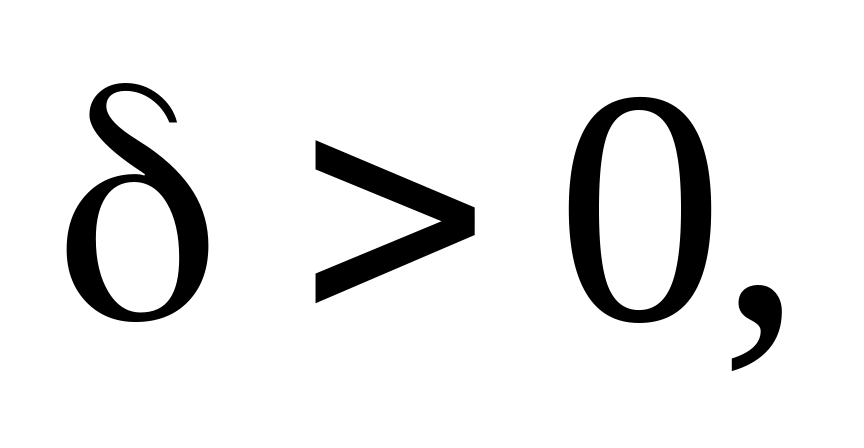 що нерівність
що нерівність
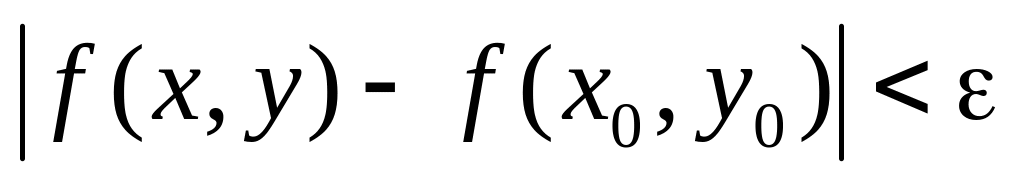
виконується
для будь-якої точки
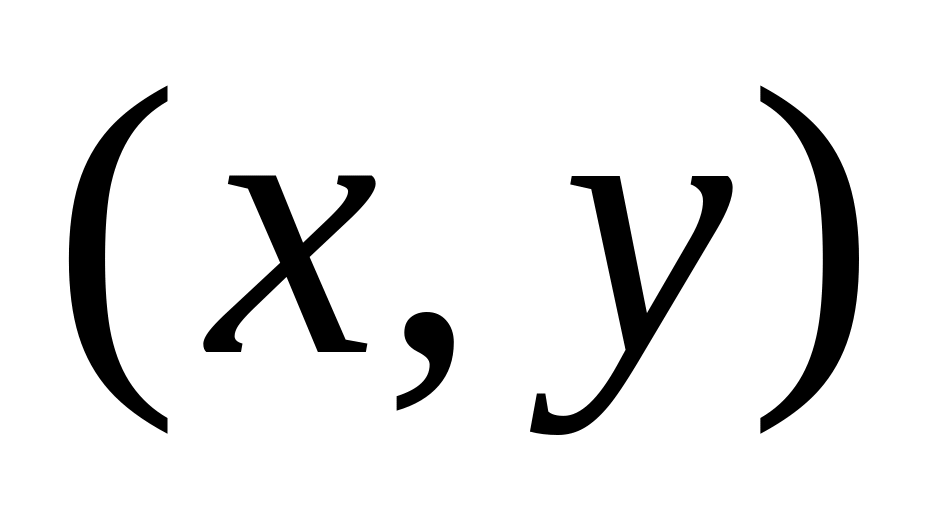
М,
яка перебуває в
-околі
точки
М,
яка перебуває в
-околі
точки
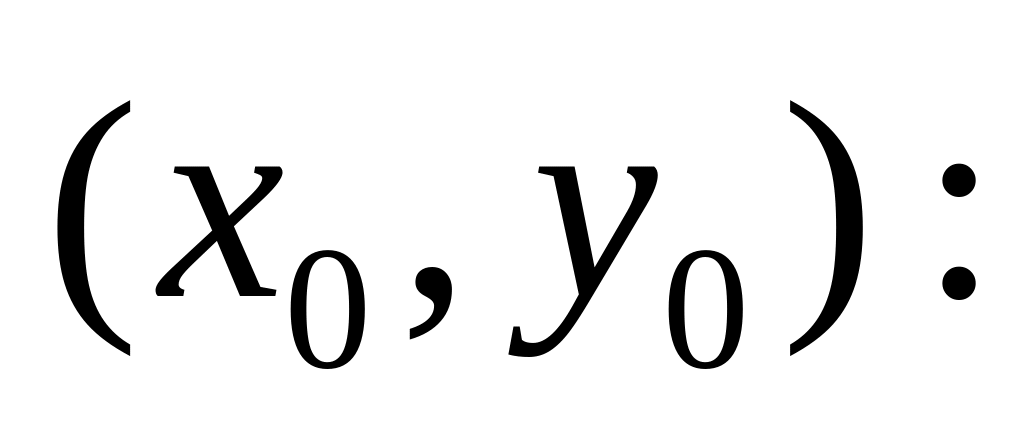
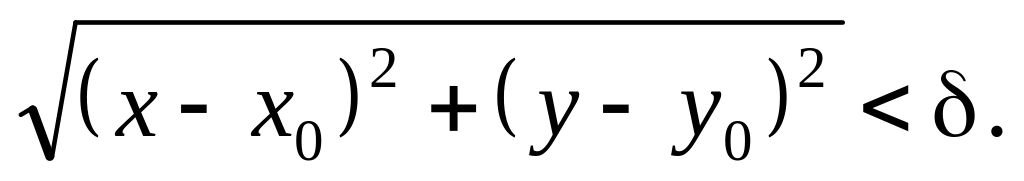
Нехай
функція
неперервна в усій множині М.
Тоді постає запитання: чи можна за даним
знайти таке
яке годилося б — у зазначеному розумінні
— для всіх точок
з М
одночасно? Якщо це можливо (при будь-якому
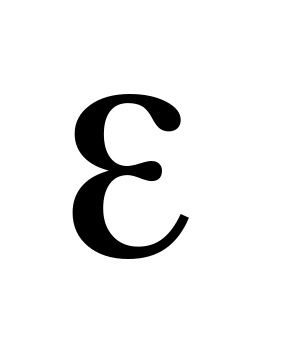 ),
тоді говорять, що функція
в М
рівномірно
неперервна.
),
тоді говорять, що функція
в М
рівномірно
неперервна.
Теорема
1.14. Якщо
функція
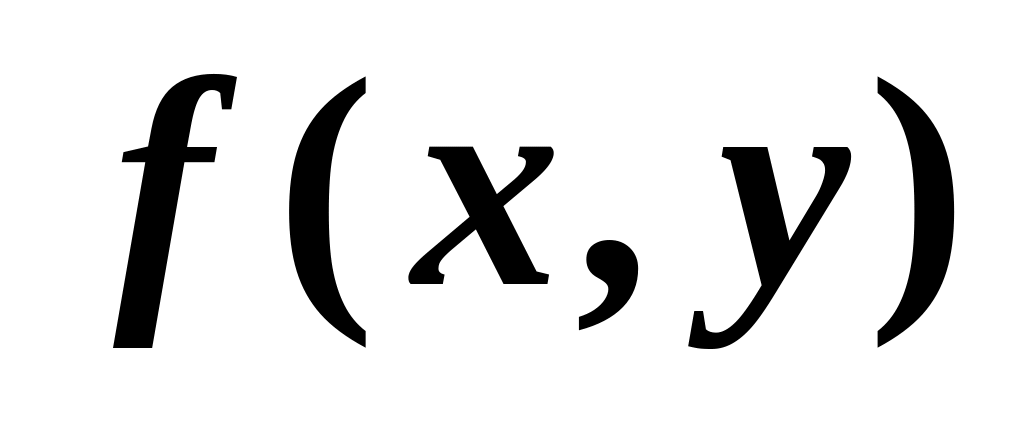 неперервна в обмеженій замкненій області
D,
то вона й рівномірно неперервна в
D.
неперервна в обмеженій замкненій області
D,
то вона й рівномірно неперервна в
D.
Доведення
(від супротивного). Припустимо, що для
деякого числа
не існує числа
яке годилося б одночасно для всіх точок
області
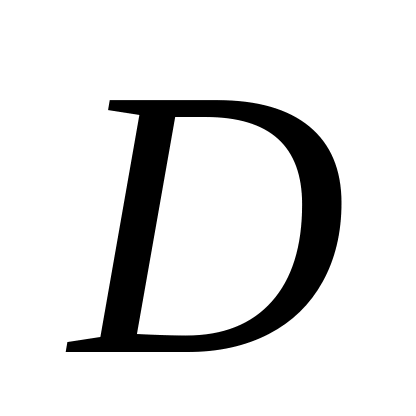 .
.
Візьмемо
послідовність додатних чисел, що прямує
до нуля:
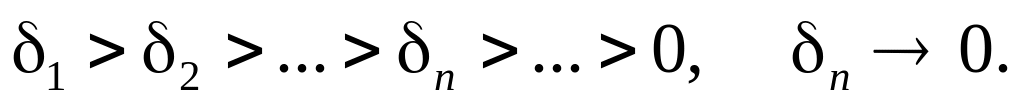
Оскільки
жодне з чисел
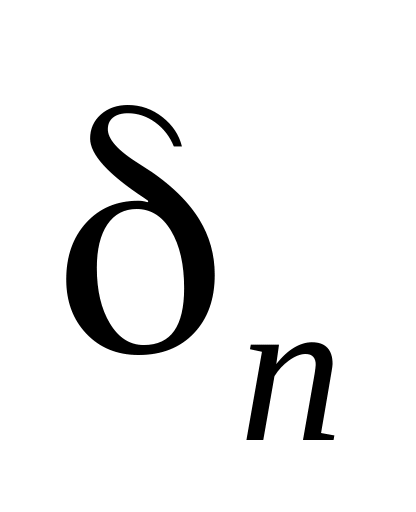 не може годитися — у зазначеному
розумінні — одночасно для всіх точок
області D,
то для кожного
не може годитися — у зазначеному
розумінні — одночасно для всіх точок
області D,
то для кожного
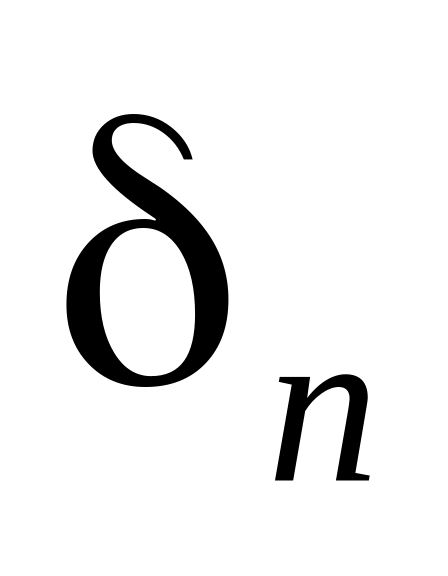 знайдеться в D
така конкретна точка
знайдеться в D
така конкретна точка
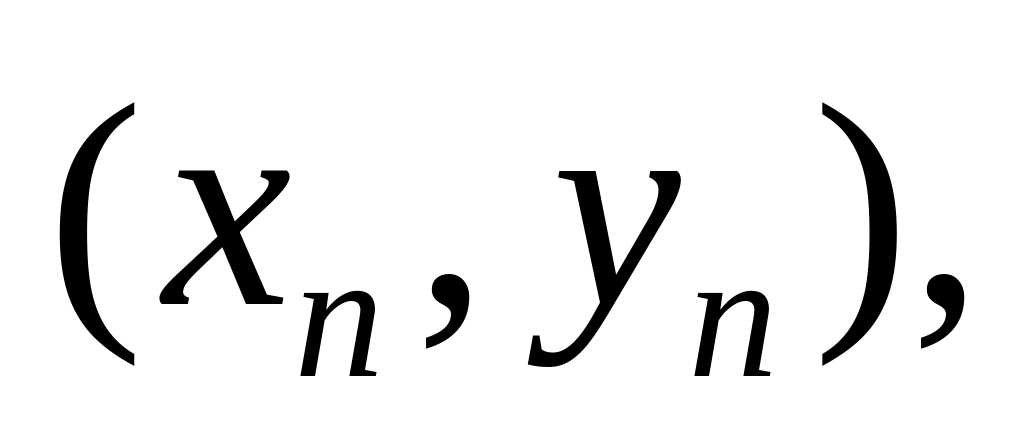 для якої
не годиться. Це означає, що в D
існує точка
для якої
не годиться. Це означає, що в D
існує точка
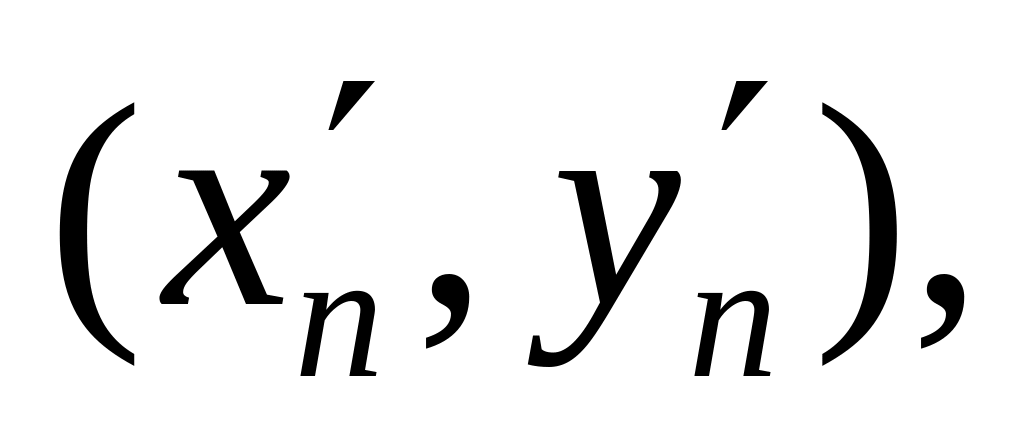 така, що виконуються нерівності
така, що виконуються нерівності
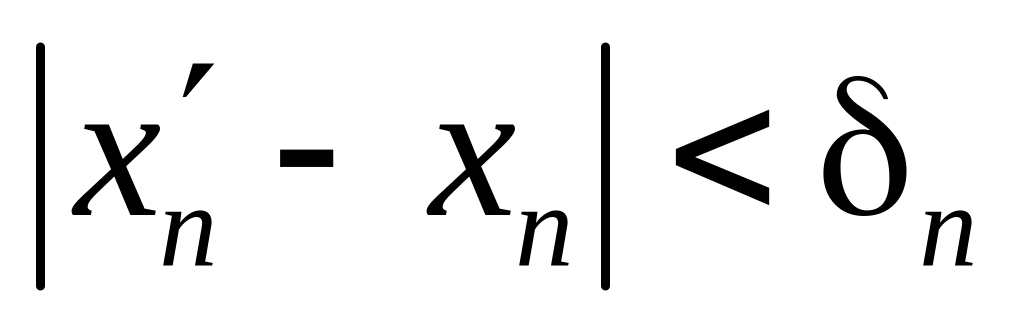 ,
,
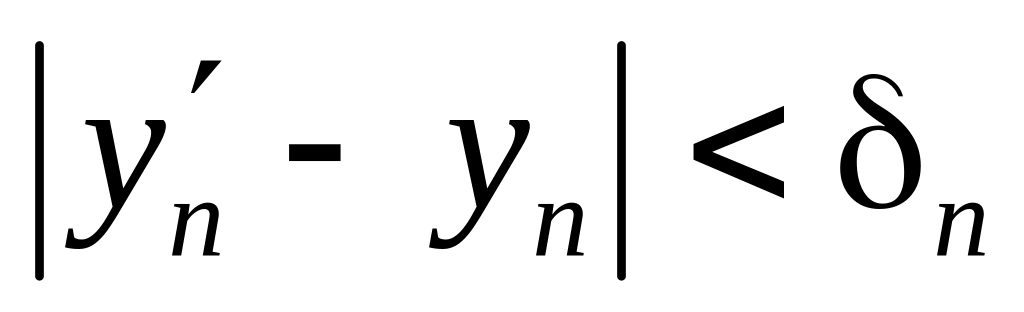 ,
,
а
водночас і нерівність
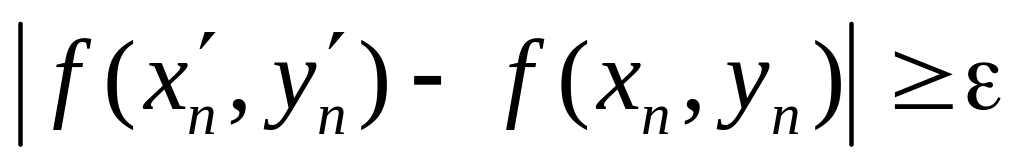 . (10)
. (10)
З
обмеженої послідовності точок
 ,
за теоремою Больцано — Вейєрштрасса,
вилучимо таку частинну послідовність
,
за теоремою Больцано — Вейєрштрасса,
вилучимо таку частинну послідовність
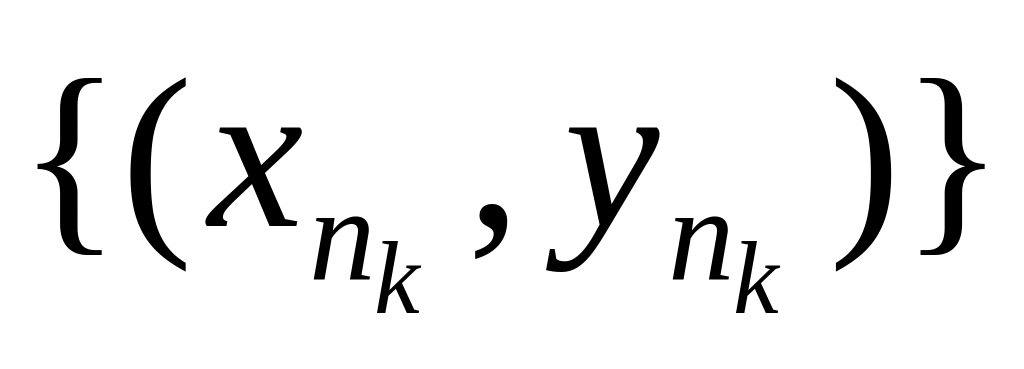 ,
що
,
що
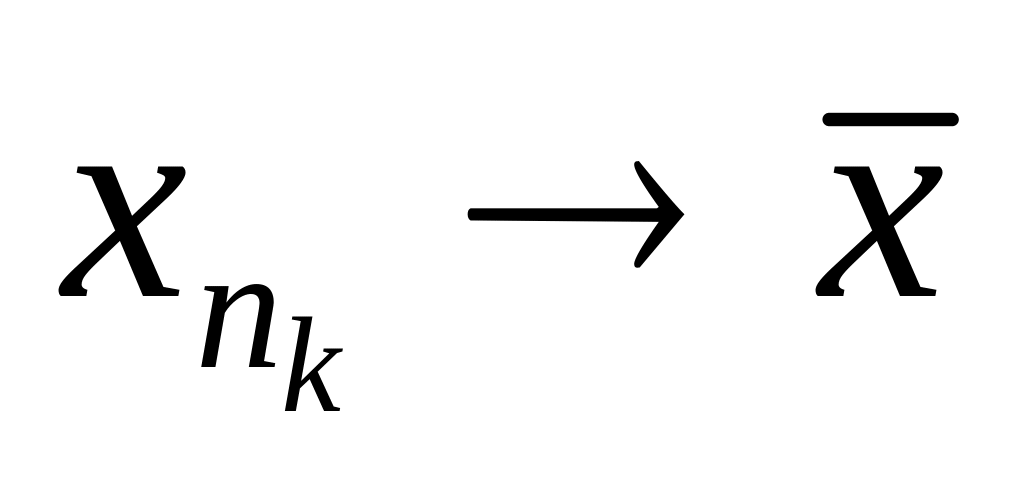 ,
,
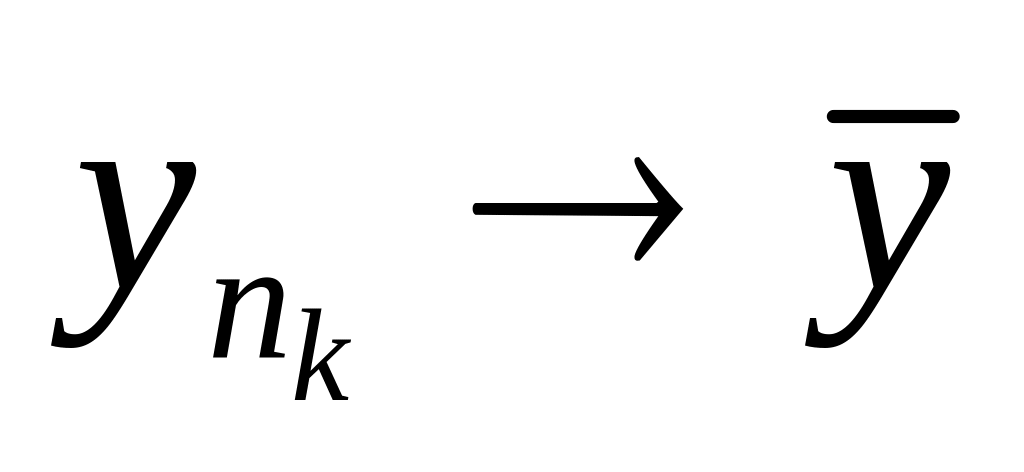 ,
причому гранична точка
,
причому гранична точка
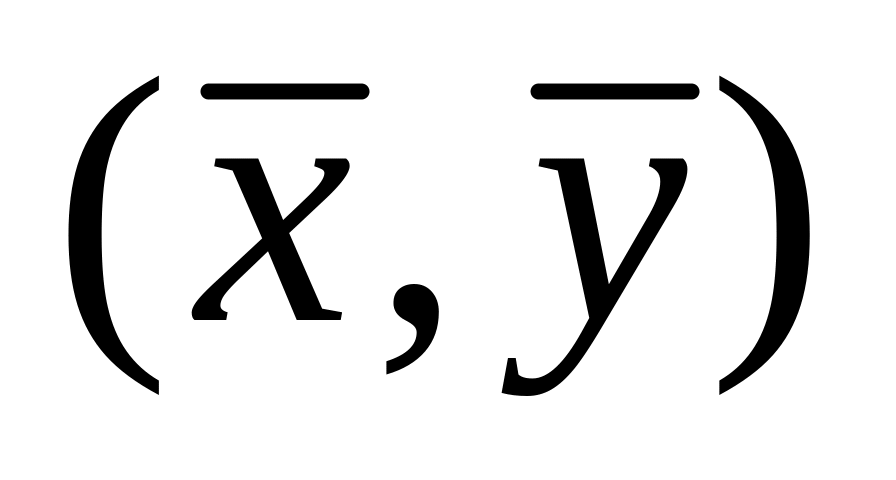 необхідно належить області D
(згідно з її замкненістю).
необхідно належить області D
(згідно з її замкненістю).
Далі
дістаємо:
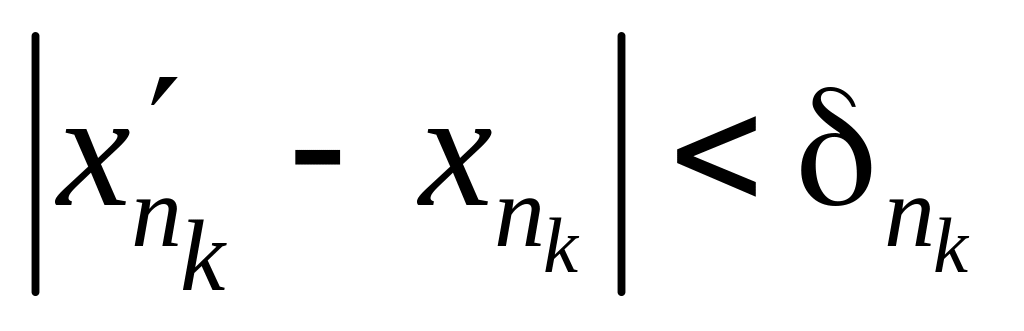 ,
,
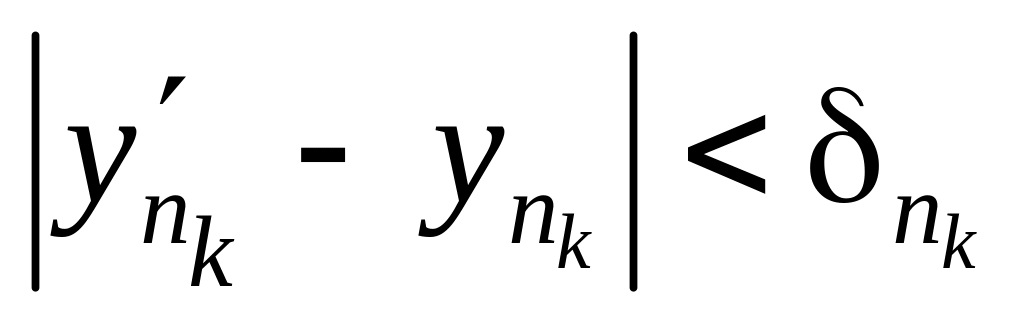 ;
;
причому
зі зростанням k
маємо:
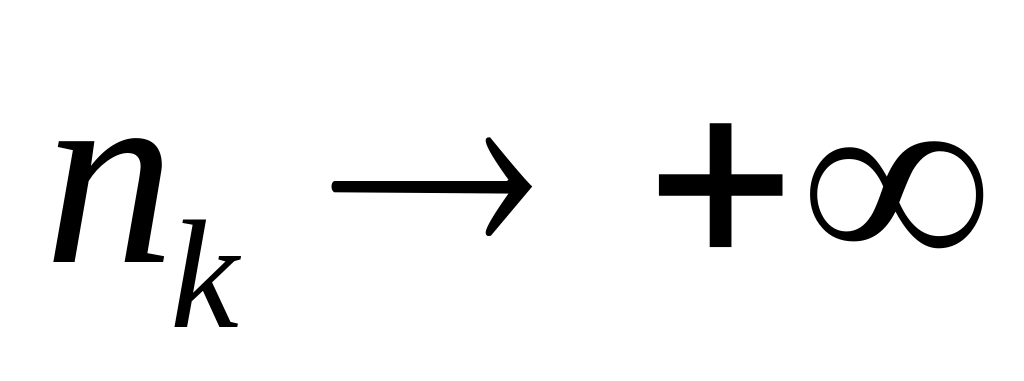 і
і
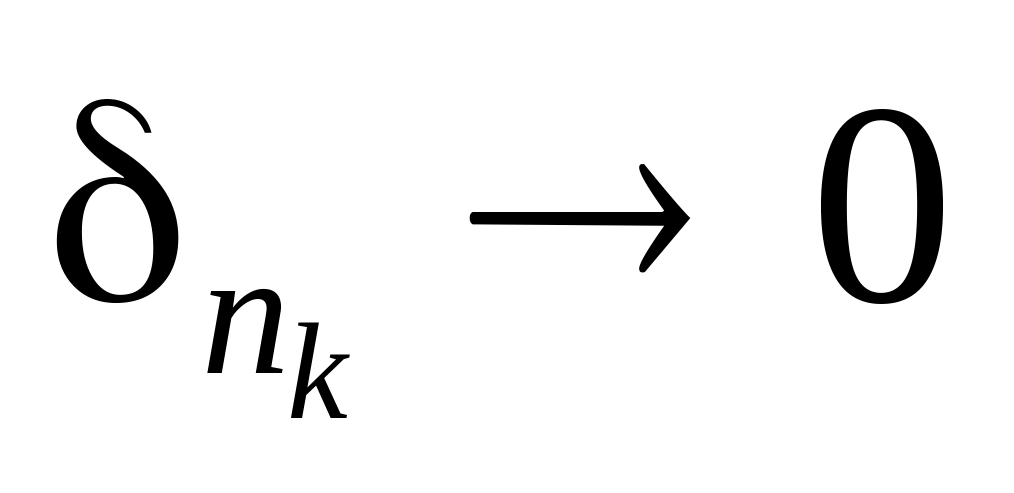 .
Тому
.
Тому
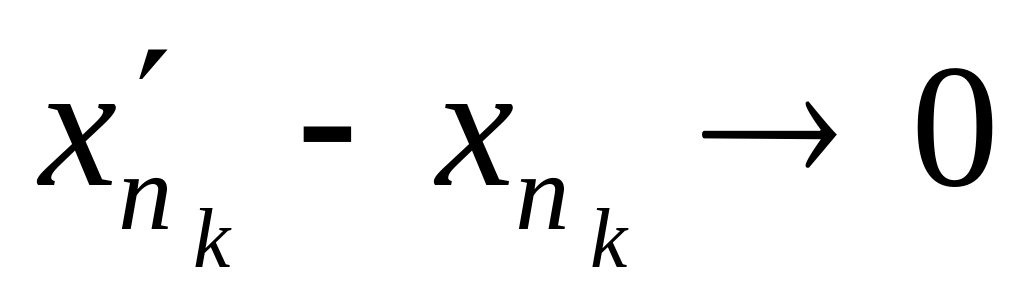 ,
,
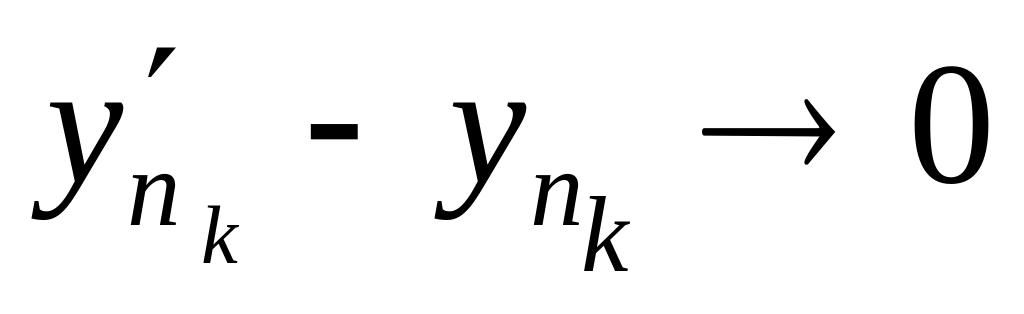 ,
,
а
отже,
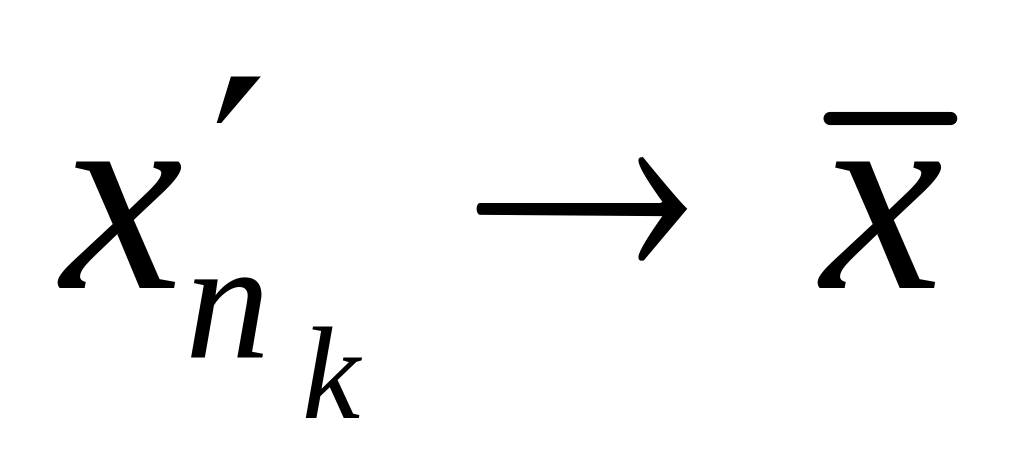 ,
,
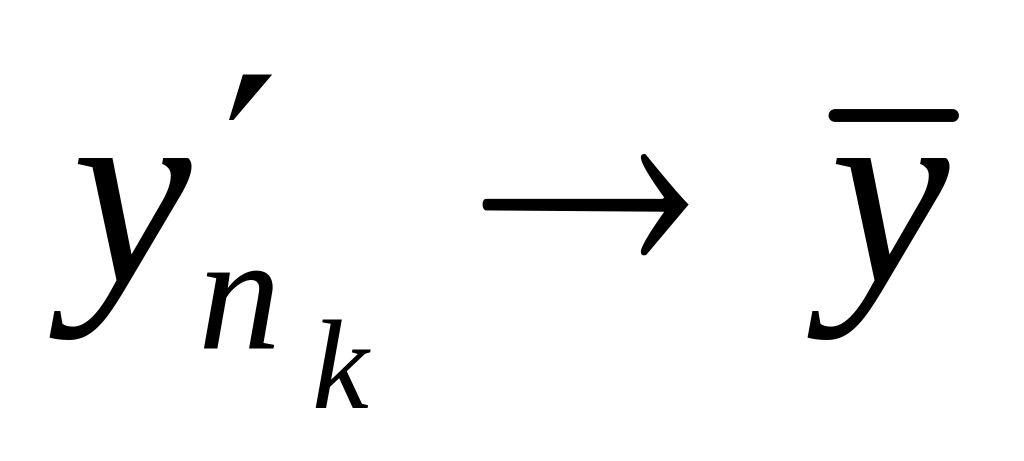 .
.
З
огляду на неперервність функції
в точці
,
що належить області
D,
мають одночасно виконуватися такі
співвідношення:
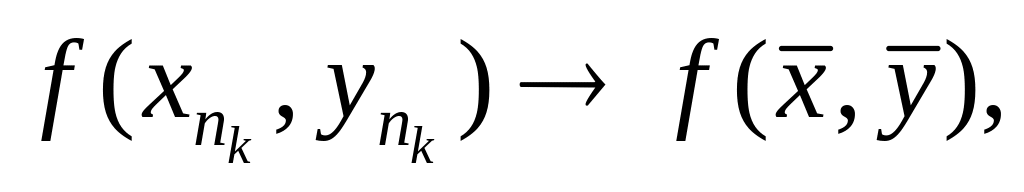
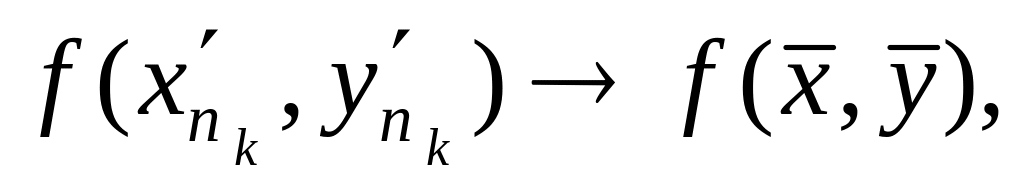
звідки
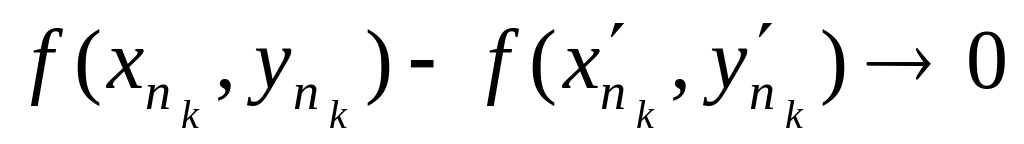 ,
,
а
це суперечить нерівності (10). Теорему
доведено
30

