21.14. Контактні явища у металах

а). Робота виходу. Метал являє собою кристалічну решітку. При утворенні кристала атоми зближаються на такі відстані, що відбувається перекриття зовнішніх ( валентних ) та внутрішніх електронних орбіталей. При цьому перекриття валентних орбіталей настільки значне, що валентні електрони одного атома охоплюють сусідні атоми і таким чином вони сколективізуються у газ ‘вільних’ електронів: кожен із них належить усім атомам одночасно і вони можуть вільно переміщуватися в межах кристала. У вузлах кристалічної решітки розміщуються іонізовані таким чином атоми, які знаходяться у тепловому коливальному русі. Вільні електрони можуть рухатися у періодичному полі кристала під дією зовнішнього електричного поля, створюючи електричний струм. Вільні електрони мають ще назву електронів провідності. При Т> 0 К, за рахунок теплової енергії кТ (кінетична енергія), вільні електрони мають можливість виходити за поверхню кристала і повертатися у кристал за рахунок кулонівських сил тяжіння до іонів. При цьому кінетична енергія електрона переходить у потенціальну енергію кулонівської взаїмодії і навпаки.

За деякий час установлюється динамічна рівновага між кількістю електронів, що вийшли за поверхню кристала, і кількістю електронів, що повернулися у кристал. Така рівновага підтримує над поверхнею кристала електронну хмарку із середнім зарядом та потенціалом (див. Мал.235). Одночасно на поверхні кристала індукується некомпенсований додатній заряд та потенціал іонів кристалічної решітки тої ж величини, що й в електронної хмарки , . Таким чином над поверхнею кристала створюється подвійний потенціальний бар’єр. Для того щоб електрон вийшов за поверхню кристала, необхідно виконати роботу проти кулонівських сил тяжіння F₊, яка викликана поверхневим зарядом q₊ та сили відштовхування , яка створюється зарядом електронної хмарки _. Ця робота дорівнює

,

д е поверхнева різниця потенціалів.

б). Закони Вольта для контактної різниці потенціалів. Для сполучених провідників Вольт установив такі закони:

1. При сполученні двох провідників, виготовлених із різнорідних металів, між точками поблизу їх поверхонь (точки В і С) виникає зовнішня контактна різниця потенціалів, величина якої залежить виключно від їх хімічної природи та температури.

2. Різниця потенціалів між точками поблизу поверхонь кінців ланцюга, створеного зєднанням різнорідних провідників, що мають однакову температуру, не залежить від хімічного складу проміжних провідників і дорівнює зовнішній контактній різниці потенціалів, що виникає при безпосередньому з’єднанні крайніх провідників.

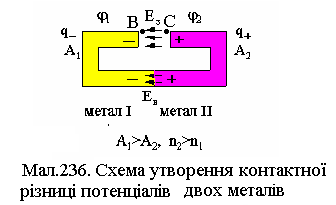
Першопричиною виникнення контактної різниці потенціалів є власні неоднакові роботи виходу металів. При з’єднанні таких провідників у місці контакту відбуваються переходи частини електронів із металу з меншою роботою виходу у метал із більшою роботою виходу (глибшою потенціальною ямою). При цьому метал з заряджається негативно, а метал з - позитивно (див. Мал.236). Цей процес триває до вирівнювання роботи виходу обох металів. При цьому різниця потенціалів визначається так

. (1)

Різниця потенціалів (1) називається зовнішньою контактною різницею потенціалів. Вона створює між вільними кінцями провідників електричне поле напруженістю .

Крім того, різні метали мають різні концентрації n_і, а тому і різні енергії Фермі. При електрони з другого металу дифундують у перший. Цей процес продовжується до вирівнювання концентрацій електронів на границі контакту в обох металах. Розрахунки внутрішньої контактної різниці потенціалів за класичною теорією можна провести у такий спосіб.

При утворенні контакту двох металів з різними концентраціями вільних електронів, через їх границю починається дифузія електронів. Через деякий час концентрації електронів при границі вирівняються а метали будуть мати потенціали . З класичної точки зору концентрацію електронів у потенціальному електричному полі з відповідним потенціалом при поверхні розділу двох металів за Больцманом можна записати у виді

, (2)

де деякі сталі, Т – температура на границі. З (2) можна одержати вирази для потенціалів

. (3)

Внутрішня контактна різниця потенціалів тепер запишеться так

. (4)

Відношення сталих має величину

,

а тому можна записати

. (5)

За порядком величини

.

З квантової точки зору, переміщення електронів у прошарку контакту змінює положення рівнів Фермі та в провідниках. У провідникові, що заряджається позитивно, рівень Фермі знижується, а у метала, що заряджається негативно - підвищується. Процес продовжується до вирівняння рівнів Фермі. Таке явище виникає у зв’язку зі зміною концентрацій електронів, від значення яких залежить величина енергії Фермі. Розглянутий процес спричиняє виникнення внутрішньої різниці потенціалів

. (3)

При Т=0 К енергія Фермі має вид

,

а підстановка цього виразу у (3) дає

.

При Т 0 К енергія Фермі має вид

.

З останнього виразу видно, що внутрішня контактна різниця потенціалів залежить від температури квадратично, але залишається досить малою величиною.

П отрібно зауважити, що у зоні контакту шириною м метали, внаслідок дифузії електронів, заряджуються різнойменно. Однак це не створює потенціального бар’єру для проходження струму у зоні контакту, як це є у напівпровіднику, тому що концентрація вільних електронів практично не змінюється.

Вираз (1) дає пояснення суті першого закону Вольта, а для пояснення другого закону розглянемо потенціали на границях металів, з'єднаних у ланцюг, як це представлено на Мал.237. Різницю потенціалів між крайніми металами при їх поверхнях (точки В і С) можна записати у вигляді

і тепер , що й пояснює другий закон Вольта.