2.7 Вектор обратной решетки

В ряде случаев бывает удобно, наряду с пространственной решеткой, вводить вспомогательную систему точек, называемую обратной решеткой. Вектор обратной решетки определяем как:

, (2.6)

где m₁, m₂, m₃ — целые числа,

, , .

Определим скалярное произведение . Для этого воспользуемся свойством дистрибутивности скалярного произведения. Тогда

, (2.7)

аналогично,

, (2.8)

(2.9)

Следовательно, имеем

, (2.10)

где N — целое число.

Если существует некоторая функция , обладающая периодичностью кристаллической решетки, т.е.

, (2.11)

то она может быть разложена в обобщенный ряд Фурье:

. (2.12)

Очевидно, что

, (2.13)

откуда следует, что

, (2.14)

, (2.15)

где N — целое число.

Можно сделать вывод, что .

Функция, обладающая периодичностью кристаллической решетки, может быть разложена в ряд по плоским волнам с волновыми векторами, являющимися векторами обратной решетки.

Пространство векторов обратных решеток – пространство волновых векторов, возможных в данной решетке. Пространство обратной решетки является частным случаем фазового пространства (так как ).

Одно из возможных применений обратной решетки — описание распределения дифракционных максимумов, получающихся при рассеянии рентгеновских лучей, электронов или нейтронов на кристалле.

В случае одномерной цепочки атомов с периодом а (см. рисунок 2.27) , вектор обратной решетки .

Рисунок 2.27 – Одномерная цепочка атомов с периодом а

Тогда ячейка Вигнера-Зейтца для такой решетки имеет границы ; .

Ячейка Вигнера-Зейтца для обратной решетки носит название первой зоны Бриллюэна. Таким образом, первой зоне Бриллюэна соответствуют . При данном значении N уравнение (2.10) определяет кристаллическую плоскость, перпендикулярную вектору обратной решетки и находящуюся на расстоянии от начала координат. Действительно,

, (2.16)

где - угол между векторами ;

- проекция вектора на вектор .

Тогда

(2.17)

При данных значениях N и G правая часть (2.17) постоянная, поэтому условие (2.17) определяет плоскость, перпендикулярную к и удаленную на расстояние 2N/G от начала координат. Если на этой плоскости лежит один узел прямой решетки, определяемый вектором , то на этой же плоскости лежит бесконечное число других узлов прямой решетки, что представлено на рисунке 2.28

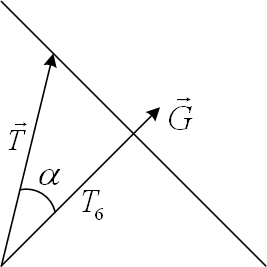
Рисунок 2.28 – Пример построения вектора по заданному вектору

Так как N — любое целое число, то вектор определяет семейство параллельных плоскостей прямой решетки, перпендикулярных к . Увеличение N на 1 приводит к увеличению на . Поэтому расстояние между соседними кристаллическими плоскостями, перпендикулярными к , равно .