
- •Предмет физики твердого тела
- •2 Периодические структуры
- •2.1 Химическая связь и кристаллическая структура
- •2.2 Кристаллическая решётка
- •2.3 Симметрия кристаллов
- •2.4. Пространственные группы и кристаллические классы.
- •2.5 Обозначение узлов, плоскостей и направлений в кристалле.
- •2.6. Плотно упакованные структуры
- •2.7 Вектор обратной решетки
- •2.8 Определение структуры кристаллов
- •3. Дефекты в кристаллах и механические свойства твердых тел
- •3.1 Дефекты кристаллов
- •3.2 Механические свойства твердых тел
- •3.3 Диффузия и ионная проводимость в твердых телах
- •4 Динамика кристаллической решетки
- •4.1 Колебания кристаллической решетки
- •4.2 Понятие о фононах
- •4.3 Теплоемкость кристаллов
- •5 Зонная теория кристаллов твердых тел
- •5.1 Электрон в периодическом поле кристалла
- •5.2 Образование энергетических зон
- •5.3 Зонная структура металлов, полуметаллов и диэлектриков
- •5.4 Электрон в кристалле как квазичастица
- •6 Металлы
- •6.1 Классическая электронная теория металлов
- •Квантовая статистика электронов в металле
- •7 Полупроводники
- •7.1 Собственные полупроводники
- •7.2 Примесные полупроводники
- •7.3 Фотопроводимость полупроводников
- •7.4 Люминесценция
7 Полупроводники
К
полупроводникам относятся материалы,
у которых валентная зона полностью
заполнена, а зона проводимости полностью
пуста при температуре абсолютного нуля.
Удельное сопротивление полупроводников
составляет
![]() Ом·м; концентрация носителей заряда
Ом·м; концентрация носителей заряда
![]() см-3
и увеличивается с ростом температуры.
см-3
и увеличивается с ростом температуры.
Полупроводники делятся на собственные и примесные.
7.1 Собственные полупроводники
 Химически
чистые полупроводники называются
собственными. К ним относятся ряд чистых
химически элементов (германий, кремний,
селен и др.) и многие химические соединения,
такие, как арсенид галлия (GaAs), арсенид
индия (InAs), антимонид индия (InSl) и др. На
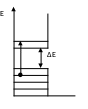
рисунке 7.1 приведена зонная структура
собственного полупроводника.
Химически
чистые полупроводники называются
собственными. К ним относятся ряд чистых
химически элементов (германий, кремний,
селен и др.) и многие химические соединения,
такие, как арсенид галлия (GaAs), арсенид
индия (InAs), антимонид индия (InSl) и др. На
рисунке 7.1 приведена зонная структура
собственного полупроводника.
Рисунок 7.1 - Зонная структура собственного полупроводника
При
повышении температуры вследствие
термического возбуждения часть электронов
валентной зоны приобретает энергию,
достаточную для преодоления запрещенной
зоны, и переходит в зону проводимости.
В результате перехода появляются две
квазичастицы с положительными эффективными
массами – электрон и дырка, причем
![]() .
Электроны из зоны проводимости и дырки
в валентной зоне могут принять участие
в проводимости. Таким образом, проводимость
полупроводников является проводимостью
возбужденной: она появляется под
действием внешних факторов, способных
сообщить электронам валентной зоны
энергию, достаточную для переброски их
в зону проводимости (такими факторами
являются нагревание полупроводников,
облучение их светом и др.). Электроны в
зоне проводимости и дырки в валентной
зоне подчиняются статистике Ферми-Дирака,
т.е. для электронов в зоне проводимости
запишем:
.
Электроны из зоны проводимости и дырки
в валентной зоне могут принять участие
в проводимости. Таким образом, проводимость
полупроводников является проводимостью
возбужденной: она появляется под
действием внешних факторов, способных
сообщить электронам валентной зоны
энергию, достаточную для переброски их
в зону проводимости (такими факторами
являются нагревание полупроводников,
облучение их светом и др.). Электроны в
зоне проводимости и дырки в валентной
зоне подчиняются статистике Ферми-Дирака,
т.е. для электронов в зоне проводимости
запишем:
 .
(7.1)
.
(7.1)
Пусть
![]() – среднее число дырок в одном квантовом
состоянии, тогда
– среднее число дырок в одном квантовом
состоянии, тогда
![]() .
(7.2)
.
(7.2)
Это равенство обусловлено тем, что каждое состояние занято либо электроном, либо дыркой. Тогда имеем
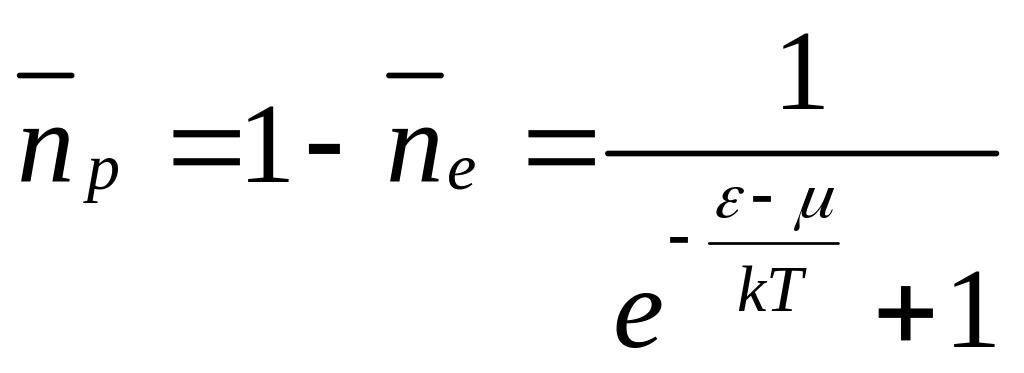 .
(7.3)
.
(7.3)
Ввиду
того, что ширина запрещенной зоны в
полупроводнике
![]()
kT,
то вероятность перехода электрона из
валентной зоны в зону проводимости
достаточно мала, а значит малы и
kT,
то вероятность перехода электрона из
валентной зоны в зону проводимости
достаточно мала, а значит малы и
![]() и
и
![]() .
Но если
<<
1 и
<<1,
то можно пренебречь единицей по сравнению
с экспонентой и записать:
.
Но если
<<
1 и
<<1,
то можно пренебречь единицей по сравнению
с экспонентой и записать:
![]() ,
,![]() .
(7.4)
.
(7.4)
Полученные соотношения представляют собой функции распределения Максвелла-Гольдмана, т.е. распределение по энергиям частиц классического идеального газа.
Таким образом, при небольших концентрациях свободных электронов и дырок, что наблюдается в полупроводниках, эти частицы образуют невырожденный электронный и дырочный газ, свойства которого подобны свойствам идеального газа.
Концентрации электронов и дырок определяются соотношениями:
![]() ;
;
![]() .
(7.5)
.
(7.5)
Здесь энергия электронов ε отсчитывается от дна зоны проводимости; энергия εp дырок отсчитывается от потолка валентной зоны вниз. За нулевой уровень энергии примем дно зоны проводимости. Концентрация электронов в зоне проводимости равна:
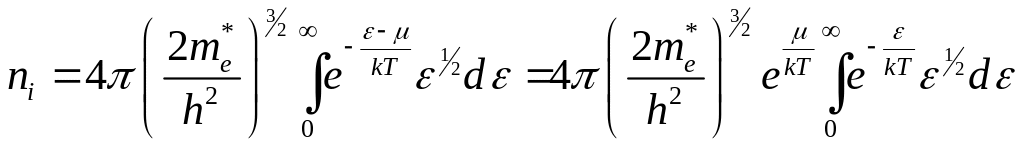 .
(7.6)
.
(7.6)
Так
как с ростом ε
функция
![]() спадает
очень быстро, то верхний предел E1
здесь заменен на ∞. Интеграл вида
спадает
очень быстро, то верхний предел E1
здесь заменен на ∞. Интеграл вида
 ,
(7.7)
,
(7.7)
тогда
![]()
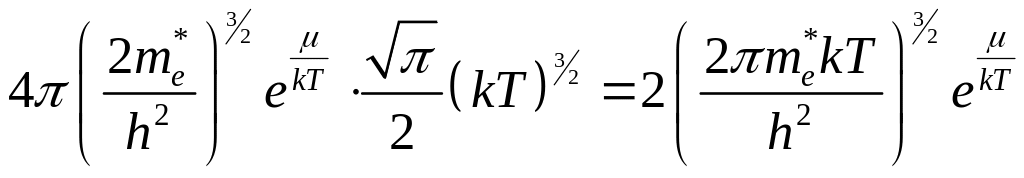 .
(7.8)
.
(7.8)
Отметим,
что для невырожденного газа
![]() .
Аналогично, для концентрации дырок в
валентной зоне запишем:
.
Аналогично, для концентрации дырок в
валентной зоне запишем:
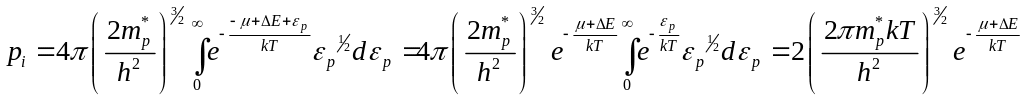 .(7.9)
.(7.9)
Найдем
произведение
![]() :
:
![]() .
(7.10)
.
(7.10)
Таким
образом, при фиксированной температуре
произведение
![]() для данного полупроводника является
величиной постоянной.
для данного полупроводника является
величиной постоянной.
В
собственных полупроводниках
![]() ,
следовательно, можно записать:
,
следовательно, можно записать:
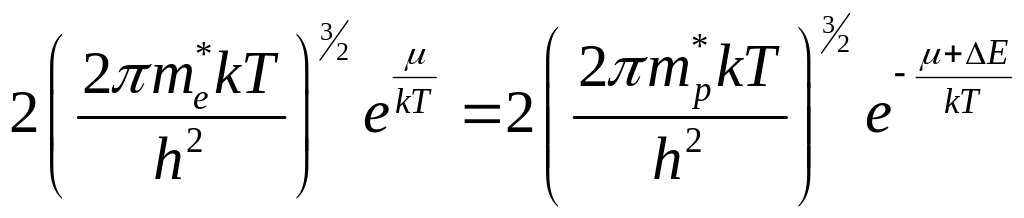 ,
(7.11)
,
(7.11)
откуда получаем
![]() ,
,
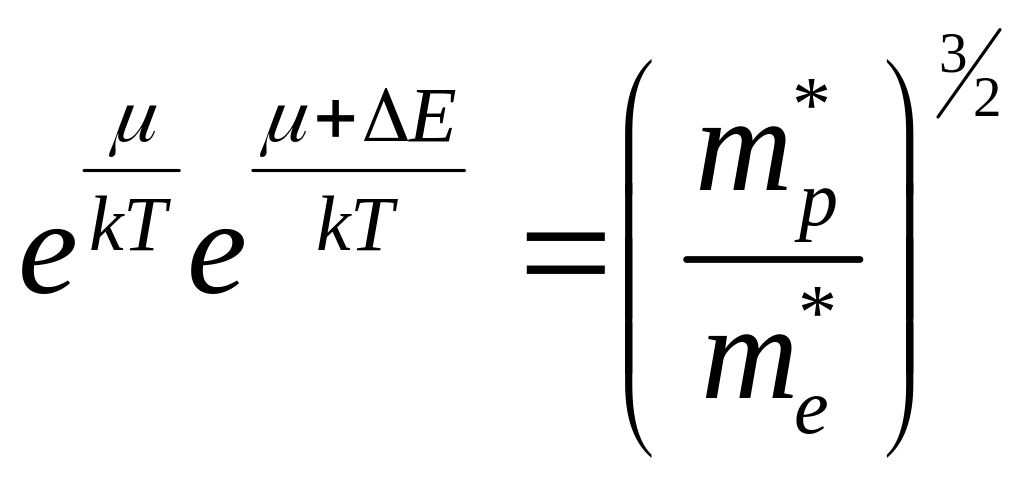 ,
,
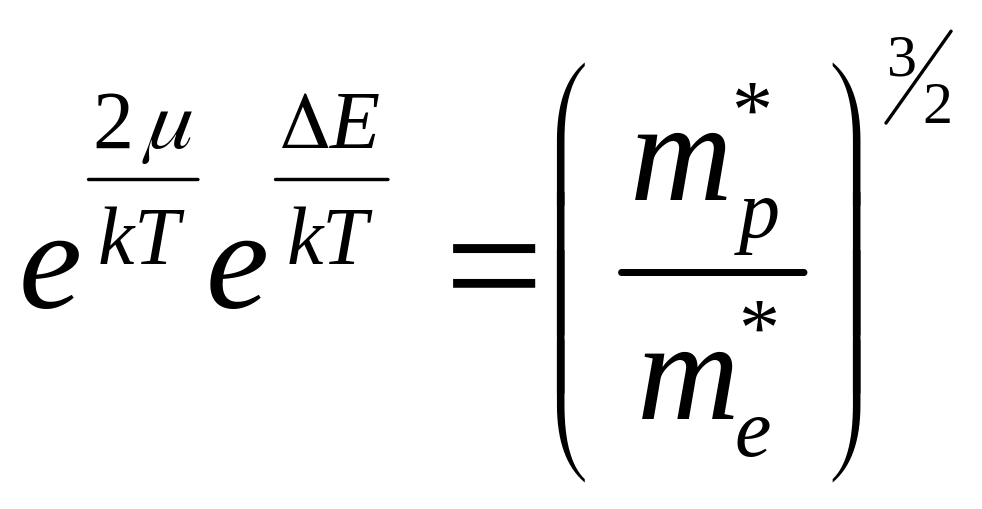 ,
,
тогда
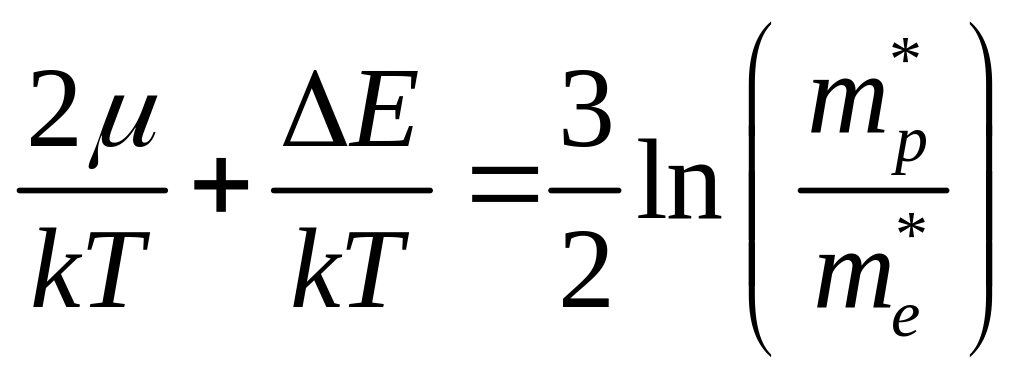 ,
,
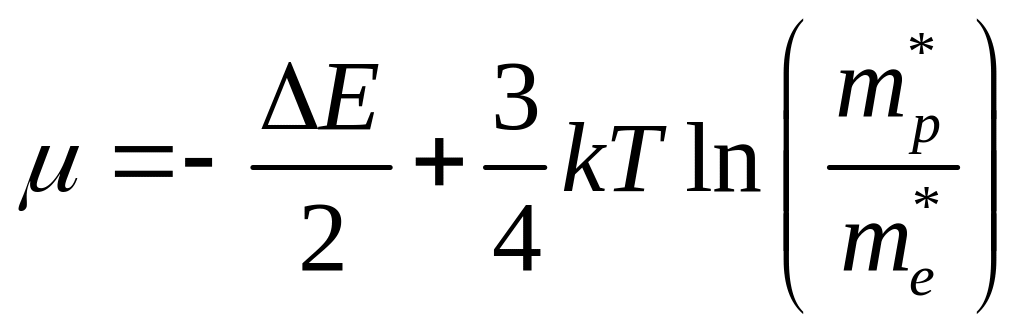 .
(7.12)
.
(7.12)
Соотношение определяет положение уровня Ферми в собственных полупроводниках. При абсолютном нуле (T=0 К) имеем:
![]() ,
(7.13)
,
(7.13)
т.е.
уровень Ферми располагается посередине
запрещенной зоны. С повышением температуры
он смещается вверх к дну зоны проводимости
(если
![]() ),
или вниз к потолку валентной зоны (если
),
или вниз к потолку валентной зоны (если
![]() ).
Как правило,
и поэтому уровень Ферми располагается
ближе к зоне проводимости. Однако в
большинстве случаев смещение уровня
Ферми невелико и им можно пренебречь.
Тогда для концентрации электронов и
дырок запишем:
).
Как правило,
и поэтому уровень Ферми располагается
ближе к зоне проводимости. Однако в
большинстве случаев смещение уровня
Ферми невелико и им можно пренебречь.
Тогда для концентрации электронов и
дырок запишем:
![]() .
(7.14)
.
(7.14)
Проводимость собственного полупроводника σ определяется соотношением:
![]() ,
(7.15)
,
(7.15)
тогда
![]() ,
(7.16)
,
(7.16)
где
![]() – элементарный заряд (заряд дырки);
– элементарный заряд (заряд дырки);
![]() и
и
![]() – подвижность электронов и дырок, причем
– подвижность электронов и дырок, причем
![]() .
.
Следовательно,
![]() ,
т.е.
,
т.е.
![]() .
(7.17)
.
(7.17)
Так как σ0 ~ T3/2, то электропроводность зависит от температуры главным образом по экспоненциальному закону. При удельная электропроводность стремится к нулю. Измеряя на опыте зависимость σ от T, можно определить ширину запрещенной зоны . Так как
![]() ,
(7.18.)
,
(7.18.)
то
в координатах
![]() и
и
![]() тангенс угла наклона прямой равен
тангенс угла наклона прямой равен
![]() .
.
