Квантовая статистика электронов в металле
Впервые квантовую статистику к электронам в металле (т.е. к электронному газу) применил Зоммерфельд.
6.2.1 Статистика Ферми-Дирака
В основе квантовой статистики лежат следующие основные положения: все электроны системы одинаковы (тождественно неразличимы); состояние электрона определяется набором квантовых чисел; в системе не может быть одновременно более одного электрона в данном квантовом состоянии (принцип запрета Паули).
Свободные электроны находятся в различных состояниях и заполняют дискретные энергетические уровни разрешенной зоны, начиная с самого нижнего. Заполнение уровней электронами задается статистикой Ферми-Дирака:
,
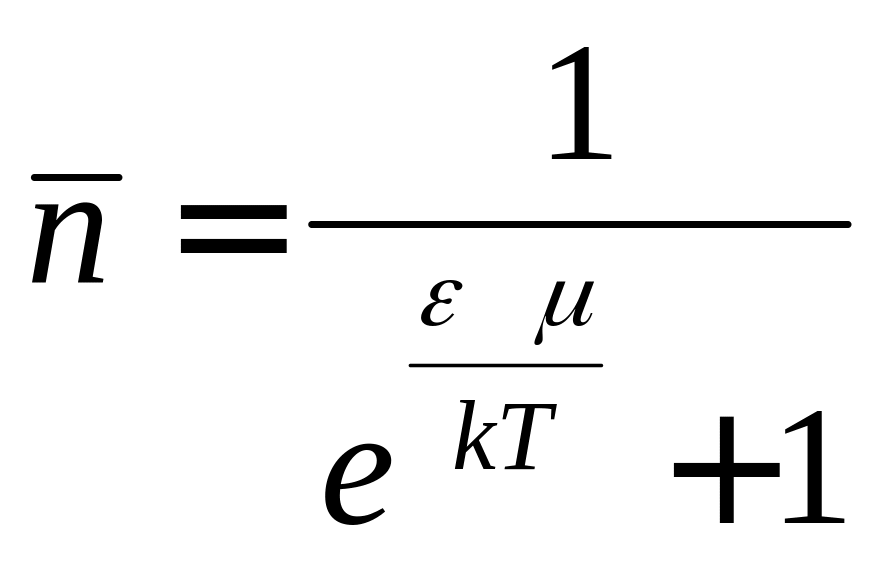(6.19)
которая
определяет вероятность заполнения
электроном энергетического уровня с
энергией
в условиях термодинамического равновесия
электронов в системе. Отметим, что если
,
то
,
если
,
то
(при этом единицей в статистике
Ферми-Дирака можно пренебречь, и
статистика Ферми-Дирака переходит в
статистику Максвелла-Больцмана). Всякое
отклонение от статистики Максвелла-Больцмана
называется вырождением. Вырождению
системы фермионов соответствует
,
при этом если
,
то газ фермионов будет средне вырожденным,
а при
говорят о сильно вырожденном газе
фермионов.
6.2.2 Полностью вырожденный электронный газ
Рассмотрим полностью вырожденный электронный газ. Полностью вырожденный электронный газ – это газ при температуре абсолютного нуля (Т=0К):
а)
если
,
то
при
.
В этом случае
;
б)
если
,
то
.
В этом случае
.
Энергия
называется уровнем Ферми (см. рис. 6.1).
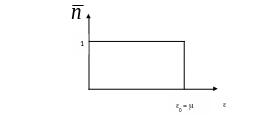
Рисунок 6.1 – Вид распределения Ферми-Дирака при Т 0
Уровень
Ферми – это такой энергетический
уровень, ниже которого все состояния
заняты, а выше которого все состояния
свободны при температуре абсолютного
нуля. При
получим
.
Определим энергию, соответствующую уровню Ферми. Для этого воспользуемся условием нормировки:
,
(6.20)
где
– число электронов, энергии которых
находятся в интервале от
до
,
(6.21)
где dΩ – число состояний с энергиями от до найдем следующим образом:
.
(6.22)
Для
одной частицы доступный фазовый объем
равен:
,
(6.23)
Тогда
.
(6.24)
Следовательно, имеем
.
(6.25)
Для фермионов необходимо учесть возможность спинового вырождения g, которое определяется формулой:
,
(6.26)
где
– спиновое число.
Для
электронов
,
тогда
.
Таким образом, можно записать:
,
(6.27)
так
как в интервале от 0
до
.
Число электронов с энергией в интервале
от
до
можно представить в виде:
,
(6.28)
тогда функция распределения примет вид:
.
(6.29)
Эту
функцию можно рассматривать как плотность
разрешенных состояний в зоне. Если
вместо
взять эффективную массу электрона
проводимости
,
то
описывает распределение энергетических
уровней в нижней части зоны проводимости.
Вообще говоря, если вместо
взять эффективную массу дырки
,
то
описывает распределение энергетических
уровней в верхней части валентной зоны.
Запишем условие нормировки:
.
(6.30)
При К имеем
,
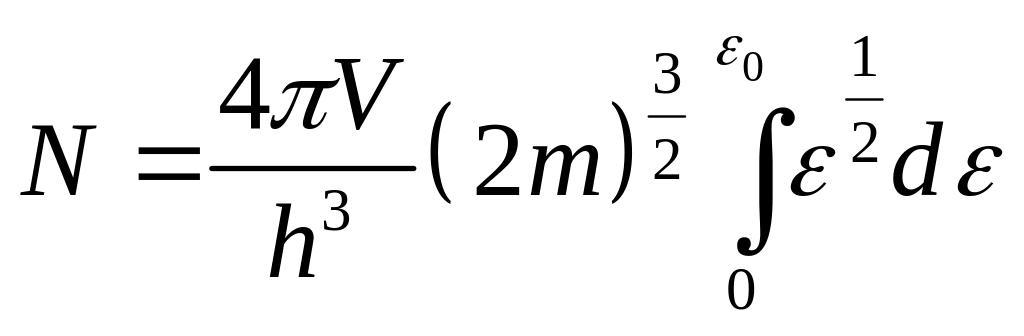(6.31)
,
(6.32)
откуда
,
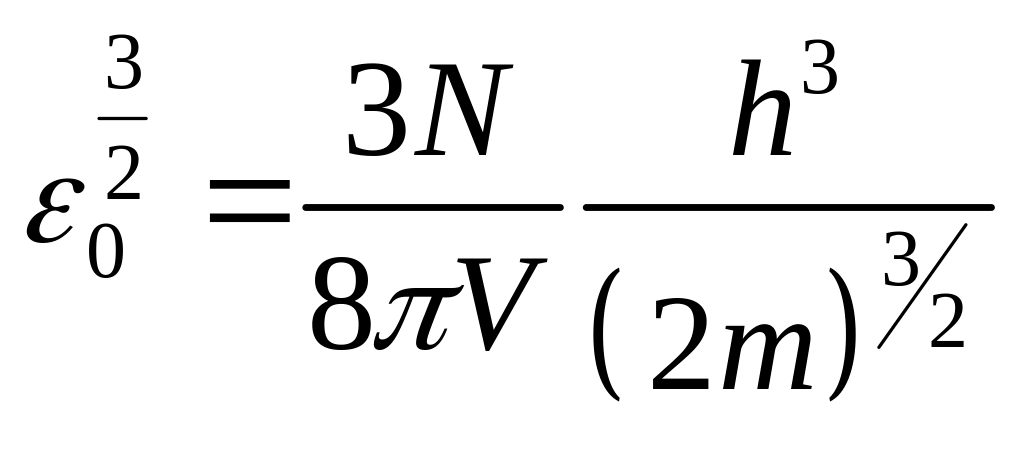(6.33)
.
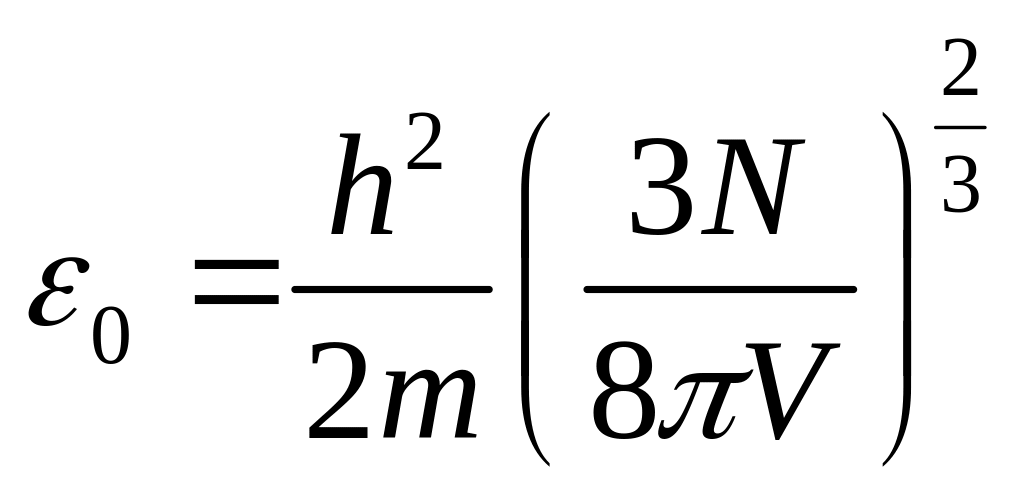(6.34)
Таким
образом, уровень Ферми пропорционален
концентрации
электронов и обратно пропорционален
массе электронов.
Зная уровень Ферми, можно определить среднюю энергию полностью вырожденного электронного газа:
.
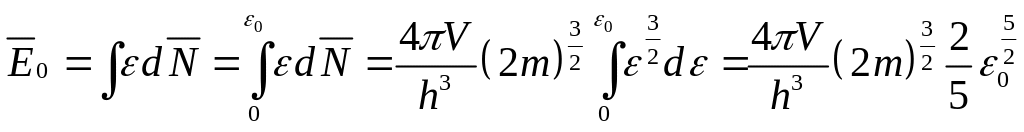(6.35)
Учитывая выражение для N (6.32), можно записать:
,
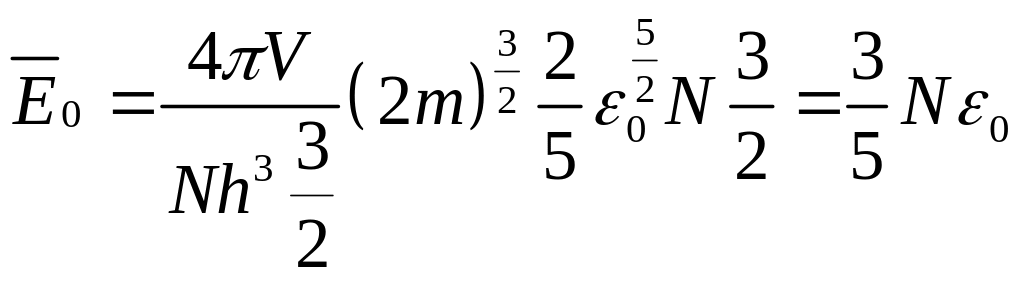т.е.
.
Можно определить давление полностью вырожденного газа. Из статистической физики известно, что уравнение состояния идеального ферми-газа имеет вид:
.
(6.36)
При Т=0К имеем:
,
(6.37)
где
–
концентрация электронного газа.
6
n
1
ε0
ε
~kT
Рисунок 6.2 – Вид распределения Ферми-Дирака при Т 0
Распределение Ферми-Дирака с ростом температуры имеет вид, показанный на рисунке 6.2.
С ростом температуры на свободные энергетические уровни переходят те электроны, энергия которых порядка уровня Ферми. Когда 0, то в тепловом движении будут принимать участие все электроны, ферми-газ перестанет быть вырожденным. Введем температуру Ферми
,
(6.38)
которая показывает, при какой температуре ферми-газ перестанет быть вырожденным:
.
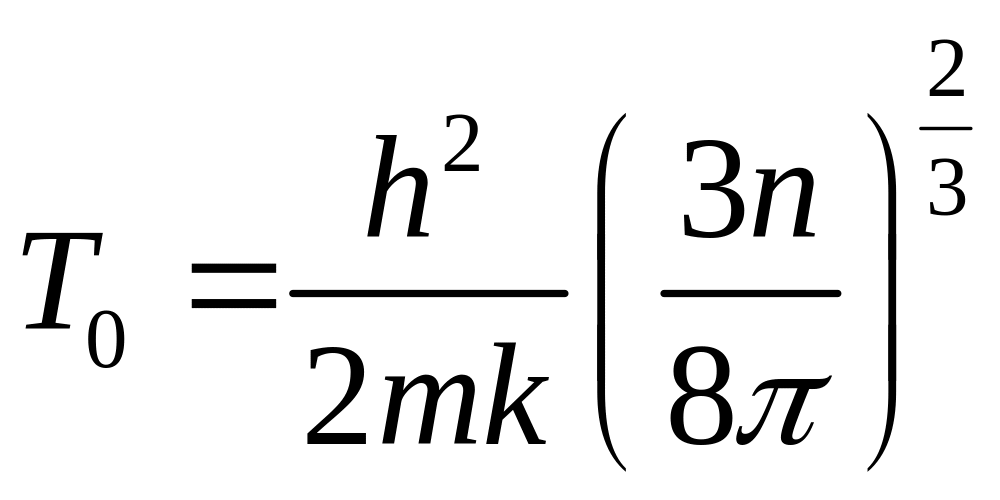(6.39)
Оценим температуру вырождения:
,
m 10-30 кг, следовательно
T0
1018
104
(K)
.
Электронный газ в металлах вплоть до температур плавления является вырожденным. Таким образом, при комнатной температуре электронный газ в металлах можно рассматривать как сильно вырожденный газ фермионов.
Зависимость химического потенциала μ от температуры можно получить из следующего выражения:
.
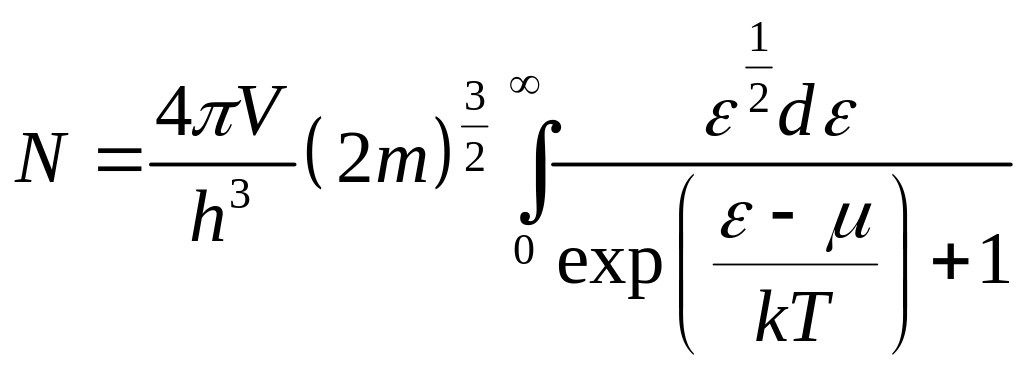(6.40)
Этот интеграл в общем случае не берется. Приближенный расчет для области температур, в которой электронный газ является еще сильно вырожденным, приводит к следующей зависимости:
.
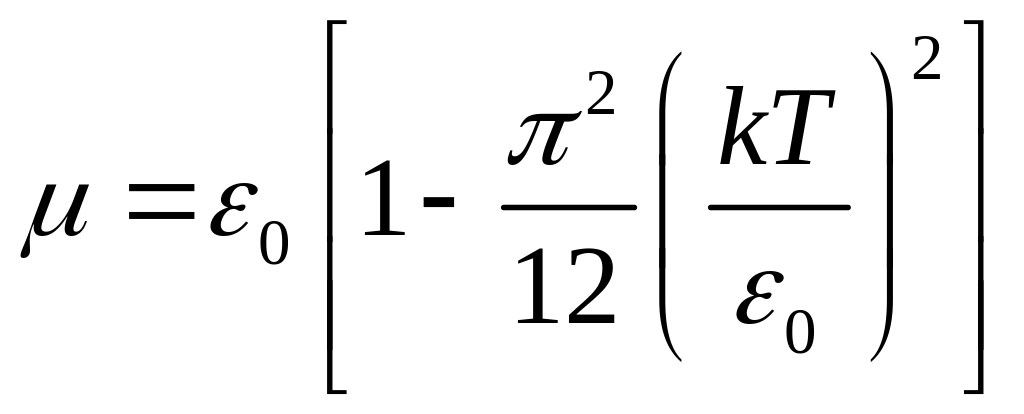(6.41)
Так
как вплоть до температуры плавления
,
то можно считать
,
т.е. уровень Ферми при любой температуре
можно считать совпадающим с
.
Построим выражение для средней энергии сильно вырожденного электронного газа:
.
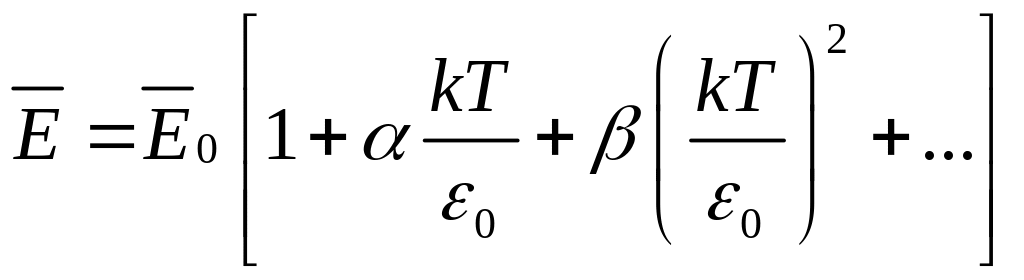(6.42)
Приближенные
вычисления средней энергии вырожденного
электронного газа дают следующие
коэффициенты:
.
Таким образом, имеем:
,
(6.43)
т.е.
.
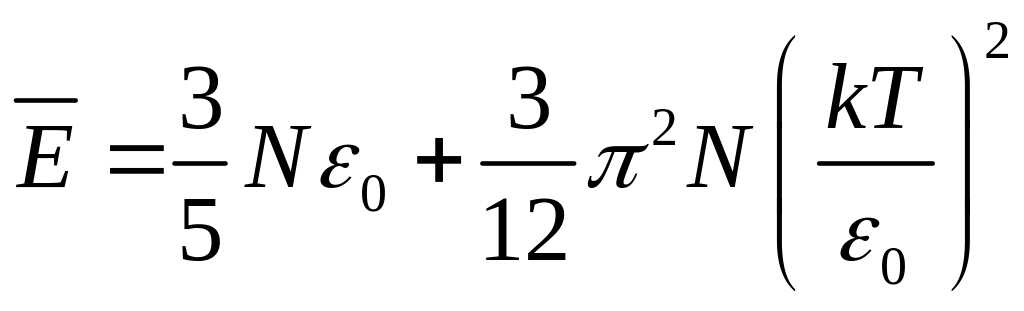(6.44)
Теплоемкость электронного газа определяется следующим соотношением:
,
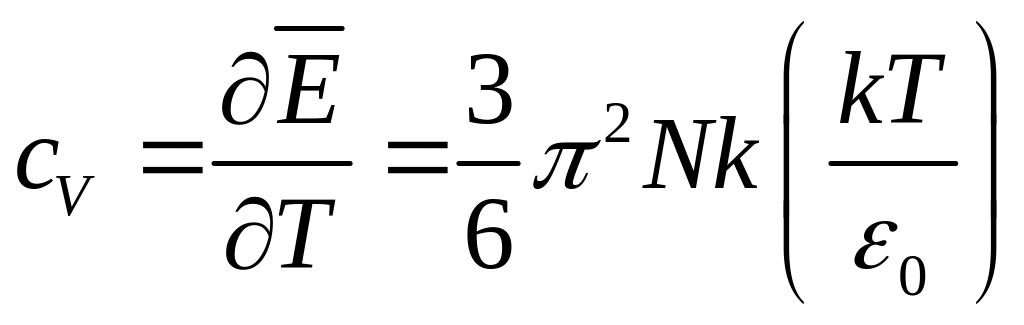(6.45)
cледовательно
сv
T. Если
бы электронный газ был бы классическим,
то его теплоемкость
.
Рассмотрим следующее соотношение:
,
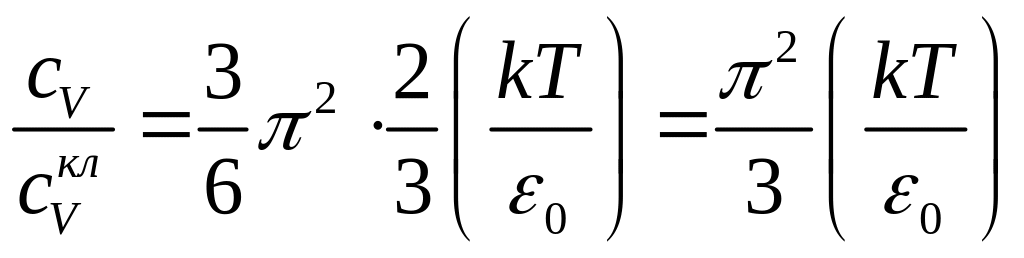(6.46)
.
Таким
образом, вследствие того, что электронный
газ в металлах является вырожденным,
термическому возбуждению даже в области
высоких температур подвергается лишь
незначительная доля свободных электронов;
остальные электроны теплоту не поглощают.
Поэтому теплоемкость электронного газа
незначительна по сравнению с теплоемкостью
решетки, и теплоемкость металла в целом
практически равна фононной теплоемкости
решетки. В области температур, близких
к абсолютному нулю, фононная теплоемкость
Т3
и вклад электронного газа может иметь
основное значение, так как
Т.
6.2.4 Теплопроводность металлов
Теплопроводность металлов, как правило, значительно больше теплопроводности диэлектриков. Это объясняется тем, что в металлах перенос тепла осуществляется главным образом свободными электронами. Механизм электронной теплопроводности можно считать аналогичным механизму фононной теплоемкости, если учесть, что в теплообмене участвуют не все электроны проводимости, а только часть их с энергиями, близкими к энергии Ферми. Тогда коэффициент теплопроводности можно представить в виде:
,
(6.47)
где
–
теплоемкость единицы объема электронного
газа.
Так как в обмене энергией с кристаллической решеткой, а следовательно, в переносе тепла участвуют только электроны с энергиями, мало отличающимися от энергии Ферми, то можно записать:
,
(6.48)
где
–
скорость электрона с энергией, близкой
к энергии Ферми. Тогда для коэффициента
теплопроводности имеем:
.
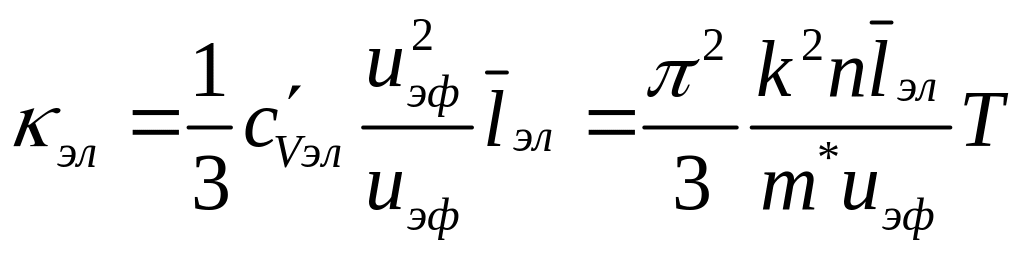(6.49)
Сравним величины коэффициентов электронной и решеточной теплопроводностей:
.
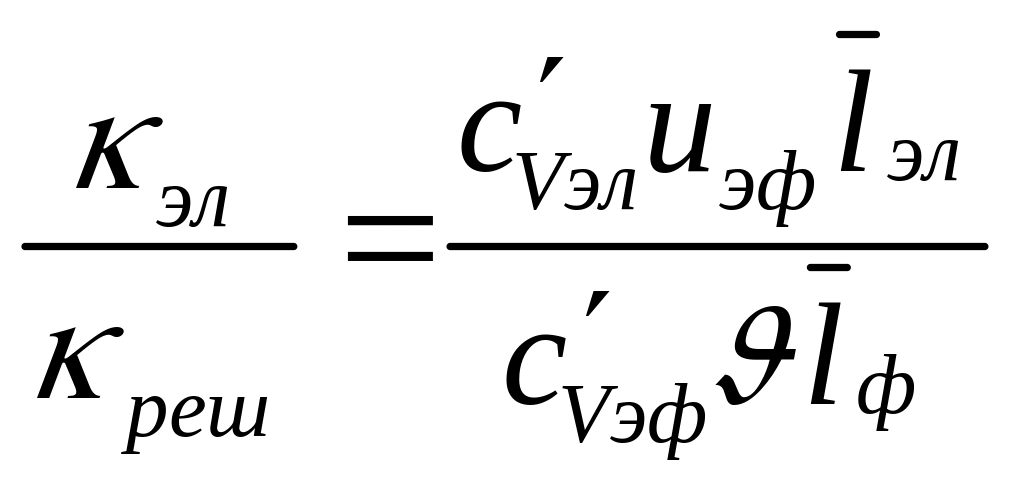(6.50)
Для
чистых металлов:
и
,
поэтому
Для
сплавов это отношение изменяется и
6.2.5 Электропроводность металлов
Под воздействием внешнего электрического поля электроны, расположенные вблизи уровня Ферми, переходят на более высокие энергетические уровни. Это означает, что в формировании электропроводности участвуют не все свободные электроны, а лишь те из них, что располагаются непосредственно у уровня Ферми.
В создании электрического тока участвуют все электроны проводимости. Вакантные состояния при действии внешнего электрического поля создаются сразу для всех электронов, так как каждый электрон, переходя в вакантное состояние, оставленное другим электроном, оставляет после себя вакантное состояние, которое замещается третьим электроном, оставляющим после себя вакантное состояние, и т.д.
Плотность электронного тока определяется выражением:
,
(6.51)
где
– функция распределения электронов в
присутствии электрического поля.
В анизотропных кристаллах, вообще говоря, вводят тензор электропроводности. В кубических кристаллах достаточно ввести одну скалярную величину – удельную электропроводность . Расчет величины удельной электропроводности металла в квантовой теории приводит к следующему выражению:
,
(6.52)
где – средняя длина свободного пробега электронов, обладающих энергиями, близкими к энергии Ферми; – их скорость.
Таким
образом, время релаксации
определяется энергией Ферми.
Длина свободного пробега определяется характером взаимодействий электронов с дефектами кристаллической решетки, которые разделяются на две группы: примеси и тепловые колебания решетки (фононы).
Так как концентрация фононов зависит от температуры, то зависимость подвижности электронов в металле и, следовательно, электропроводности от Т будет иметь сложный характер. Для чистых металлов зависимость электропроводности (и удельного сопротивления) от Т имеет вид, представленный на рисунке 6.3:
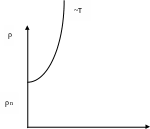
Т
Рисунок 6.3 – Вид зависимости = f(T)
а) в области высоких температур
;
(6.53)
б) в области низких температур
,
(6.54)
где А,В, α и b – коэффициенты пропорциональности.
6.2.6 Закон Видемана-Франца
В квантовой теории для закона Видемана-Франца получается следующее выражение:
.
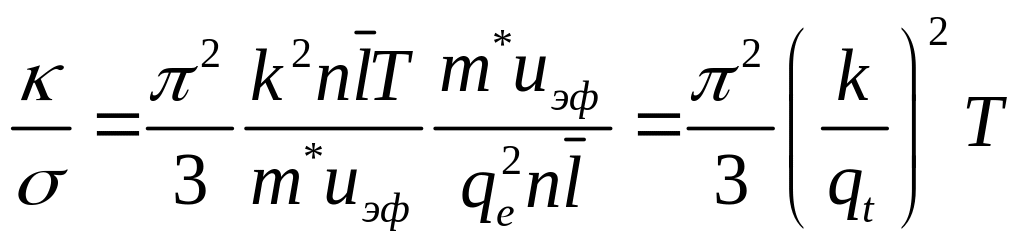(6.55)
Опыт
показывает, что закон хорошо выполняется
при температурах выше температуры Дебая
.