4.1 Колебания кристаллической решетки

С колебаниями кристаллической решетки связаны следующие свойства кристаллов:

- упругие свойства;

- тепловое расширение кристаллов;

- диэлектрическая проницаемость кристаллов;

- теплоемкость кристаллов.

4.1.1 Колебания линейного кристалла

При рассматривании колебания линейного кристалла воспользуемся двумя предположениями:

1. Будем считать, что среднее равновесное положение атомов совпадает с узлом решетки Браве. Тогда можно с каждым атомом связывать определенный узел решетки, относительно которого совершаются атомом колебания, но теперь узел есть лишь среднее положение атома, а не его фиксированное мгновенное положение.

2. Примем, что типичные отклонения каждого атома от его положения равновесия малы по сравнению с расстоянием между атомами.

Пусть кристалл состоит из атомов массой М. Количество атомов в кристалле N+1. Период кристаллической решетки равен а. Длина кристалла равна Na.

Предположим, что взаимодействуют лишь соседние атомы. При малых колебаниях справедливо гармоническое приближение, т.е.

, (4.1)

где f — жесткость связи.

Тогда сила взаимодействия

. (4.2)

Г

f

армоническое приближение соответствует модели, приведенной на рисунке 4.1.

а

Рисунок 4.1 – Модель, соответствующая гармоническому приближению

Если число N велико и если нас не интересуют эффекты, происходящие на концах цепочки, точный вид описания атомов, расположенных на ее концах, не существенен, и можно воспользоваться таким подходом, который дает наибольшее математическое преимущество. Удобнее всего выбрать периодические грани чные условия Борна — Кармана.

Колебания n- го атома кристалла описываются уравнением:

. (4.3)

В динамике решетки выбирают в качестве координат величину смещения каждого атома от равновесного положения (см. рис.4.2).

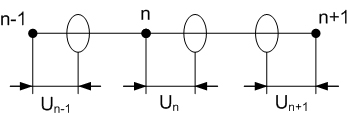
Рисунок 4.2 - Выбор координат в динамике решетки

Решение будем искать в виде:

В этом случае можно записать:

аналогично,

,

где ;

— скорость распространения упругой волны.

Следовательно, имеем:

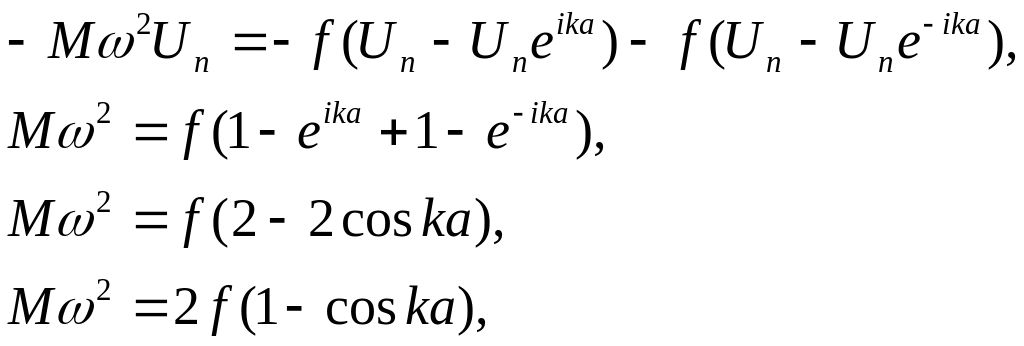
или

откуда

. (4.7)

Полученное соотношение представляет собой дисперсионное уравнение.

Если , то такие значения k не приводят к физическим различным результатам. Область значений k, приводящих к физически различным результатам, определяется выражением:

, (4.8)

т.е. значения k, приводящее к физически различным результатам, лежат в области первой зоны Бриллюэна. Из (4.8) следует, что

т.е. , откуда .

Таким образом, два соседних узла кристалла совершают колебания в противофазе, т.е. возникает стоячая волна. Дисперсионная кривая в этом случае имеет вид, приведенный на рисунке 4.3.

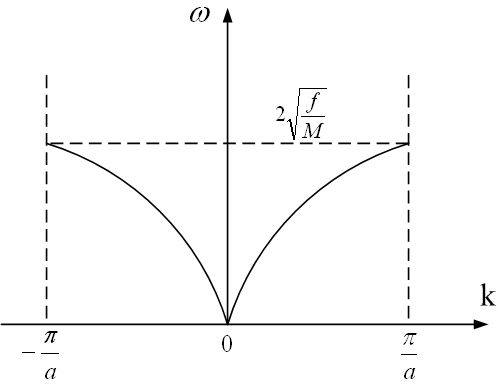
Рисунок 4.3 – Вид дисперсионной кривой ы первой зоне Бриллюэна

В кристалле могут распространяться волны с частотами от 0 до максимально возможной частоты , соответствующей минимальной длине волны .

Рассмотрим область низких частот ( ). Тогда

,

откуда

. (4.9)

Наблюдается линейная зависимость в том случае, когда длина волны велика по сравнению с расстоянием между частицами. Волна, для которой зависимость линейная, носит название акустических. При длинах волн сравнимых с расстоянием между частицами, линейный закон дисперсии перестает соблюдаться.

Фазовая скорость акустических волн равна:

, (4.10)

Групповая скорость акустических волн равна:

. (4.11)

Рассмотрим поведение дисперсионной кривой (см. рис. 4.4) на границе первой зоны Бриллюэна:

. (4.12)

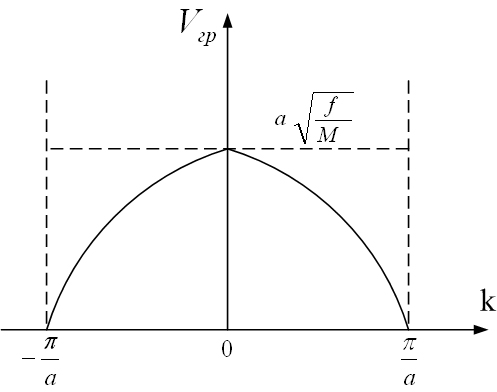
Рисунок 4.4 – Вид дисперсионной кривой на границе первой зоны Бриллюэна.

На границе первой зоны Бриллюэна происходит отражение упругой волны.

Оценим частоту колебаний :

, (4.13)

Если принять , , то .

На границе первой зоны Бриллюэна отражение испытывает не только упругие волны, но и рентгеновские, что следует из условия Лауэ.

Подсчитаем количество независимых колебаний в линейном кристалле. Так как при колебаниях частиц кристалл как целое неподвижен, то другие волны отражаются от границ кристалла, следовательно, фазы колебаний первой и последней частиц одинаковы. Общий набег фазы на длине цепочки Na равен :

, (4.14)

, , … , , (4.15)

причем большие значения к не приводят к физически различным результатам.

В линейной цепочке атомов количество не зависимых колебаний совпадают с числом атомов.

Отметим, что волновые числа k имеют дискретное значение, что связно не с квантовыми эффектами, а с образованием стоячих волн в кристаллах. Так как N >>1, то спектр значений можно считать практически непрерывным.

Полученные результаты можно распространить на трехмерный кристалл. Волновые векторы лежат в приделах первой зоны Бриллюэна. В каждом направлении в кристалле могут распространяться три акустические волны: одна продольна и две поперечные со взаимно поляризациями. В общем случае, когда ориентирован произвольно относительно направлений симметрии кристалла, волны не являются чисто продольными или чисто поперечными. Однако в приделе длинных волн (малых ), когда кристалл можно рассматривать как изотропную среду, одна волна является продольной, а две другие — поперечными. Таким образом, с учетом трех возможных направлений поляризации, всего имеется 3N состояний, что совпадает с числом степеней свободы атомов кристалла.

4.1.2 Колебания линейного кристалла с базисом

Рассмотрим колебания линейного кристалла с базисом, состоящим из двух различных атомов. Массы атомов равны M и m соответственно.

Запишем уравнение движения атомов в базисе:

, (4.16)

. (4.17)

Решение имеем в виде:

, ,

, , (4.18)

, .

Таким образом, имеем:

(4.19)

Получена система алгебраических уравнений с двумя неизвестными амплитудами:

Имеем систему линейных однородных уравнений. Система имеет нетривиальные решения, если определитель, построенный из коэффициентов, равен нулю:

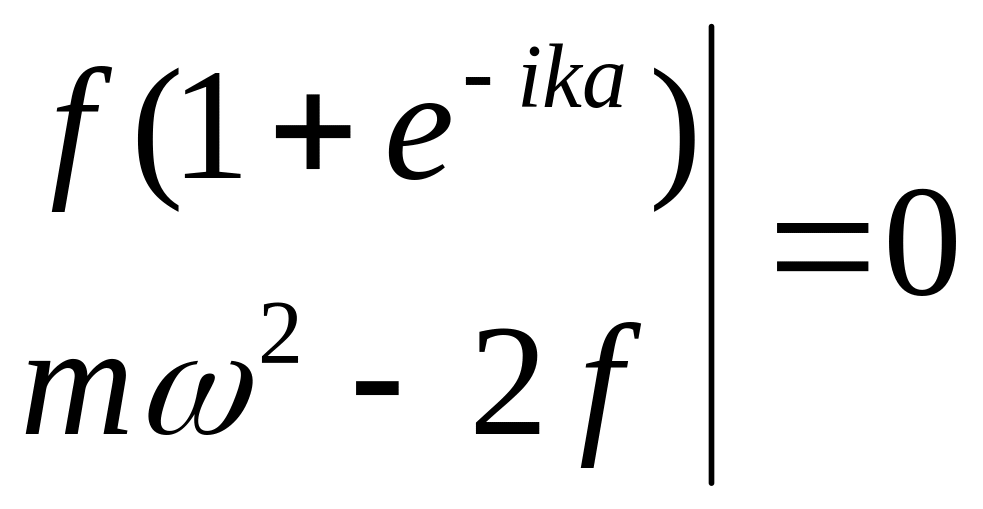, (4.20)

откуда

(4.21)

С учетом

(4.22)

(4.23)

Получим биквадратное уравнение для частот :

, (4.24)

, (4.25)

. (4.26)

Следовательно:

, (4.27)

. (4.28)

Рассмотрим значения и на границе первой зоны Бриллюэна. Так как, , то можно записать:

, (4.29)

, (4.30)

при этом необходимо иметь ввиду, что .

Как и в многоатомной цепочке атомов, периодическое граничное условие Борна-Кармана вновь приводит к N неэквивалентным значениям k .

Для каждого из N значений k имеется два решения, что дает в целом 2N нормальных колебаний (мод), как и должно быть при 2N степенях свободы. Две кривые называется двумя ветвями законно дисперсии (см. рис. 4.5).

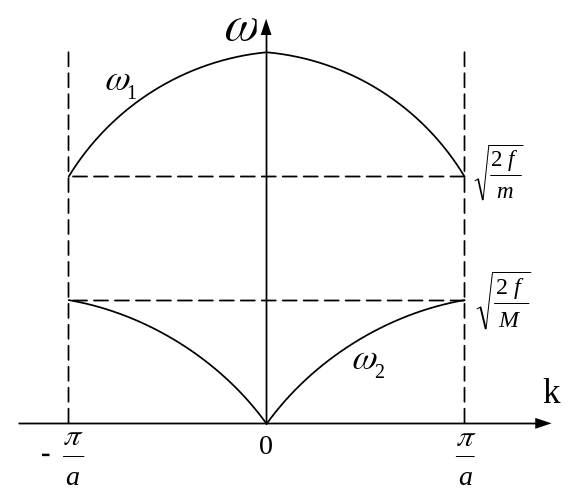
Рисунок 4.5 – Две ветви закона дисперсии

Ветвь называется акустической, потому что ее закон дисперсии при малых n имеет вид , что характерно для звуковых волн.

Действительно, при , имеем . Поскольку при x<<1, то можно записать:

, (4.31)

следовательно,

. (4.32)

При акустических колебаниях элементарная ячейка совершает колебания как единое целое.

Ветвь называется оптической ветвью (см. рис. 4.5). В этом случае соседние атомы колеблются в противоположных фазах. Эти колебания можно рассматривать как колебания друг относительно друга подрешеток из однородных атомов, вставленных одна в другую. Такая ситуация возникает при воздействии на кристалл электромагнитных волн.

Оптические колебания возникают и в том случае, если элементарная ячейка содержит два и более однородных атомов. Оптические колебания возникают в результате колебаний одной подрешетки относительно другой.

Полученные результаты можно обобщить на случай колебаний трехмерного кристалла с базисом из S атомов. Для каждого значения k имеется 3S нормальных колебаний, из них 3 ветви — акустические и 3S – 3 — оптические.