
- •Глава 4. Автоматы
- •§ 4.1. Автоматы: определение, примеры, способы задания
- •4.1.1 Определение и примеры автоматов
- •4.1.2. Диаграмма Мура и таблица автоматов
- •§ 4.2. Отличимость состояний автомата
- •4.2.1 Продолжение функций и
- •4.2.2. Приведённый автомат
- •4.2.3. Периодичность выходной последовательности конечного автомата
- •4.2.4. Теоремы Мура
- •4.3. Ограниченно детерминированные функции. Информационное дерево
- •Задачи для самостоятельного решения
- •§ 4.4. Синтез автоматов
- •Задачи для самостоятельного решения
- •§ 4.5. Алгебраический подход к теории автоматов
- •Упражнения для самостоятельного решения
§ 4.2. Отличимость состояний автомата
4.2.1 Продолжение функций и
Пусть
![]() конечный алфавит. Обозначим через
конечный алфавит. Обозначим через
![]() множество всех слов
множество всех слов
![]() Число
Число
![]() называется длиной
слова
называется длиной
слова
![]() и обозначается
и обозначается
![]() Например, если
Например, если
![]() то
то
![]()
![]()
![]() Слово, в котором нет ни одной буквы,
будем называть пустым
словом и
обозначать символом
Слово, в котором нет ни одной буквы,
будем называть пустым
словом и
обозначать символом
![]() Очевидно,
Очевидно,
![]() Пусть
Пусть
![]() множество слов длины
множество слов длины
![]() а
а
![]() множество непустых слов. Тогда
множество непустых слов. Тогда
![]()
![]()
![]()
Произведением
слов
![]() называется слово, полученное приписыванием
к слову
справа слова
называется слово, полученное приписыванием
к слову
справа слова
![]() Таким образом, если
Таким образом, если
![]()
![]() то
то
![]() Нетрудно проверить, что произведение
слов ассоциативно, т.е.
Нетрудно проверить, что произведение
слов ассоциативно, т.е.
![]() для любых
для любых
![]() Вообще, произведение слов
Вообще, произведение слов
![]() не зависит от расстановки скобок (но
зависит от порядка сомножителей). В
частности,
не зависит от расстановки скобок (но
зависит от порядка сомножителей). В
частности,
![]()
Произведение
слов некоммутативно,
так как в общем случае
![]()
Множество,
на котором задана ассоциативная операция,
называется полугруппой.
Полугруппа
![]() в которой есть единица,
т.е. такой элемент е,
что
в которой есть единица,
т.е. такой элемент е,
что
![]() для всех
для всех
![]() называется моноидом.
Множества
и
называется моноидом.
Множества
и
![]() являются полугруппами. Кроме того,
являются полугруппами. Кроме того,
![]() – моноид (так как
– моноид (так как
![]() для всех
для всех
![]() то пустое слово
то пустое слово
![]() является единицей). Полугруппа
моноидом не является; это можно доказать
так: ввиду того, что
является единицей). Полугруппа
моноидом не является; это можно доказать
так: ввиду того, что
![]() для любых
для любых
![]() то равенство
то равенство
![]() в
невозможно.
в
невозможно.
Функции
![]() и
и
![]() можно продолжить до функций
можно продолжить до функций
![]() и
и
![]() следующим образом. Положим
следующим образом. Положим
![]() при
при
![]() при
при
![]()
![]() при
при
![]() при
при
![]()
![]()
Функция
![]() несёт информацию о том, в какое состояние
перейдёт автомат, если на его вход будут
поступать последовательно несколько
букв из алфавита
несёт информацию о том, в какое состояние
перейдёт автомат, если на его вход будут
поступать последовательно несколько
букв из алфавита
![]() Действительно, если в какой-либо момент
автомат находится в состоянии
Действительно, если в какой-либо момент
автомат находится в состоянии
![]() а на его вход поступают буквы
а на его вход поступают буквы
![]() то будут осуществляться следующие
переходы в другие состояния:
то будут осуществляться следующие
переходы в другие состояния:
![]()
т.е.
в конце концов автомат окажется в
состоянии
![]() Аналогичным образом интерпретируется
функция
Аналогичным образом интерпретируется
функция
![]() А именно,
А именно,
![]() где
где
![]() буква, которая будет выдана автоматом
на
-м
шаге.
буква, которая будет выдана автоматом
на
-м
шаге.
Упражнение 5. Автомат задан таблицей
|
a |
b |
c |
|
0 |
|
1 |
|
0 |
1 |
1 |
Определить:
![]()
![]()
![]()
![]()
![]()
Решение.
![]()
![]()
![]() поэтому
поэтому
![]()
![]()
![]() поэтому
поэтому
![]()
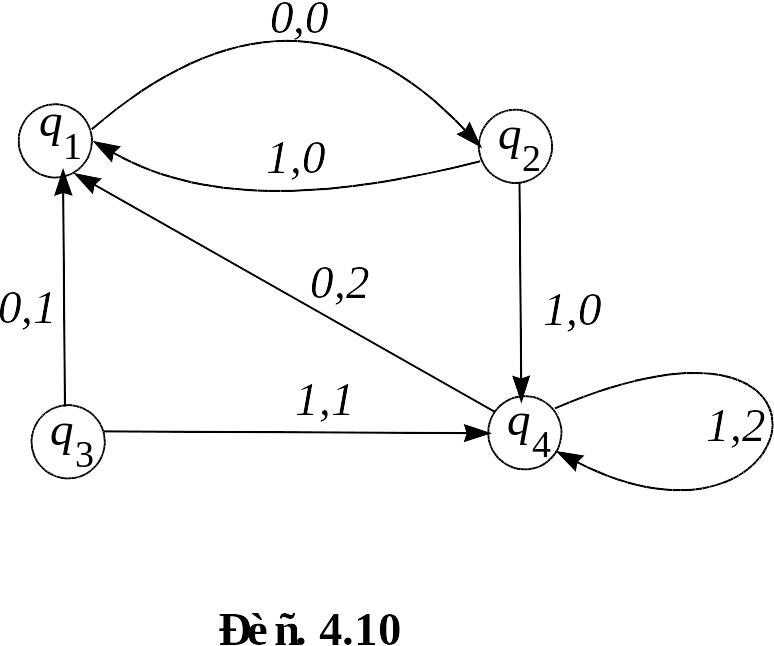
Упражнение
6. Автомат
задан диаграммой Мура, изображённой на
рисунке 4.10. Найти:
![]()
![]()
Решение.
Имеем:
![]() поэтому
поэтому
![]()
![]()
![]()
4.2.2. Приведённый автомат
Назовём
состояния
![]() и
и
![]() автомата
автомата
![]() неотличимыми,
если
неотличимыми,
если
![]() для всех
для всех
![]() Состояния
и
отличимы,
если
Состояния
и
отличимы,
если
![]() при некотором
Положим
при некотором
Положим
![]() если
и
неотличичимы. Нетрудно видеть, что
отношение неотличимости ~ на множестве
если
и
неотличичимы. Нетрудно видеть, что
отношение неотличимости ~ на множестве
![]() состояний автомата
состояний автомата
![]() является отношением эквивалентности.
Это отношение вызывает разбиение
множества
на непересекающиеся классы эквивалентности:
является отношением эквивалентности.
Это отношение вызывает разбиение
множества
на непересекающиеся классы эквивалентности:
![]() При этом любые два состояния
При этом любые два состояния
![]() лежащие в одном классе, неотличимы, а
любые два состояния из разных классов
отличимы.
лежащие в одном классе, неотличимы, а
любые два состояния из разных классов
отличимы.
Множество
классов отношения ~ (фактор-множество
![]() обозначим через
обозначим через
![]() Построим новый автомат
Построим новый автомат
![]() В качестве входного и выходного алфавитов
автомата
В качестве входного и выходного алфавитов
автомата
![]() возьмём те же множества
возьмём те же множества
![]() и
и
![]() которые были у автомата
которые были у автомата
![]() а в качестве множества состояний возьмём
множество
Надо определить теперь функции
а в качестве множества состояний возьмём
множество
Надо определить теперь функции
![]() и
и
![]()
Пусть
![]()
![]() Наиболее естественным является следующее
определение значения
Наиболее естественным является следующее
определение значения
![]() взять какой-нибудь элемент
принадлежащий классу
взять какой-нибудь элемент
принадлежащий классу
![]() найти
найти
![]() а затем класс, в котором лежит элемент
объявить значением
а затем класс, в котором лежит элемент
объявить значением
![]() То есть считать, что
То есть считать, что
![]() (1)
(1)
Можно
доказать корректность
этого определения, т.е. независимость
от выбора представителя в классе
эквивалентности. Другими словами, если
![]() то
то
![]()
Функцию
![]() определим на
определим на
![]() по формуле
по формуле
![]() (2)
(2)
По
определению неотличимости состояний
мы имеем
![]() поэтому определение (2), как и (1), корректно.
поэтому определение (2), как и (1), корректно.
Автомат
![]() называется приведённым
автоматом,
соответствующим автомату
называется приведённым
автоматом,
соответствующим автомату
![]()
У приведённого автомата любые два различных состояния отличимы друг от друга.
Автомат
и приведённый автомат
работают одинаково: для любой входной
последовательности
![]() последовательность
последовательность
![]() на выходе автомата
и автомата
одна и та же:
на выходе автомата
и автомата
одна и та же:
![]()
![]() и т.д. (здесь
и т.д. (здесь
![]() – начальное состояние).
– начальное состояние).
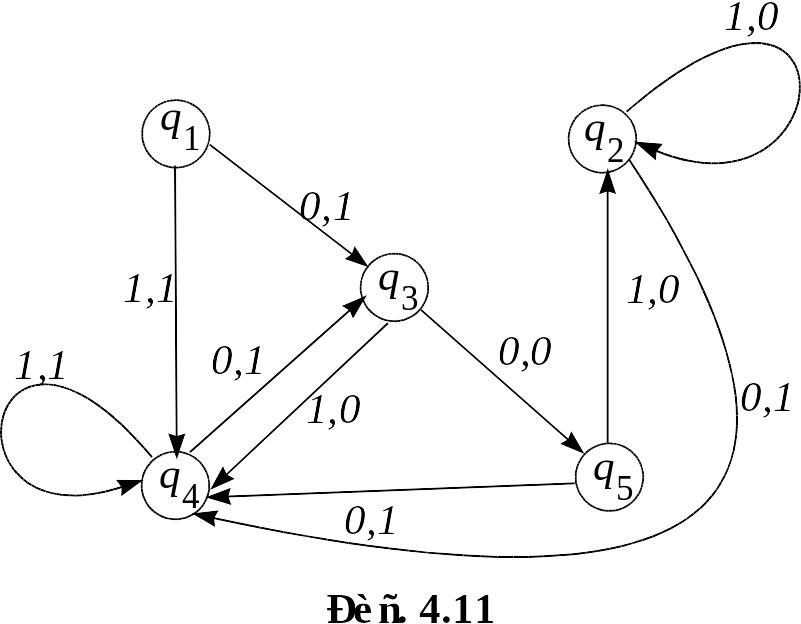
Упражнение 7. Построить приведённый автомат для автомата, заданного диаграммой Мура, изображённой на рисунке 4.11.
Решение.
Вычислим:
![]()
![]()
![]()
![]()
![]() Следовательно, состояние
отличимо от всех остальных. Мы получаем
(пока) следующее разбиение множества
Следовательно, состояние
отличимо от всех остальных. Мы получаем
(пока) следующее разбиение множества
![]() на классы, т.е. непересекающиеся
подмножества:
на классы, т.е. непересекающиеся
подмножества:
![]() (далее это разбиение будет измельчаться).
(далее это разбиение будет измельчаться).
Далее
вычисляем:
![]()
![]()
![]()
![]() Отсюда следует, что
не может лежать в одном классе с
Отсюда следует, что
не может лежать в одном классе с
![]() или
или
![]() с
или
с
или
![]() и т.д. Разбиение, полученное ранее,
измельчается до следующего:
и т.д. Разбиение, полученное ранее,
измельчается до следующего:
![]() Положим
Положим
![]()
![]()
![]() Покажем, что это окончательное разбиение.
Имеем:
Покажем, что это окончательное разбиение.
Имеем:
![]()
![]() поэтому
поэтому
![]() Аналогично получаем
Аналогично получаем
![]() и т.д., т.е. функция
и т.д., т.е. функция
![]() “не разбивает” классы. Следовательно,
классы
“не разбивает” классы. Следовательно,
классы
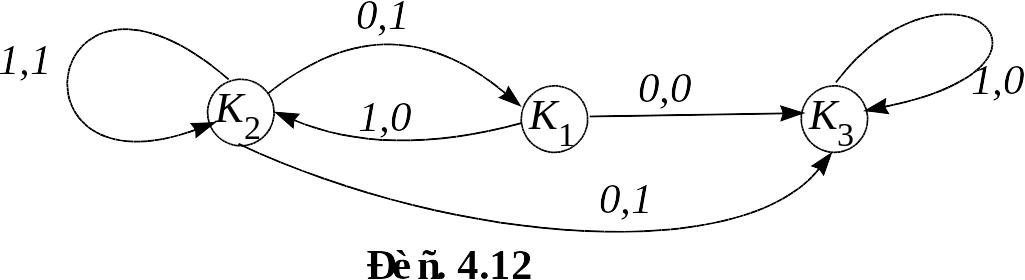
![]() можно считать состояниями нового
автомата. Это и есть приведённый автомат,
его диаграмма Мура изображена на рисунке
4.12.
можно считать состояниями нового
автомата. Это и есть приведённый автомат,
его диаграмма Мура изображена на рисунке
4.12.
Упражнение 8. Построить приведённый автомат для автомата , заданного следующей таблицей:
|
|
|
|
|
|
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
|
0 |
Решение.
Верхняя строка таблицы 11011 определяет
разбиение
![]() нижняя строка
разбиение
нижняя строка
разбиение
![]() Их пересечение
Их пересечение
![]() это разбиение
это разбиение
![]() Докажем, что состояния
Докажем, что состояния
![]() неотличимы друг от друга. В столбцах
таблицы, соответствующих этим состояниям,
мы имеем:
неотличимы друг от друга. В столбцах
таблицы, соответствующих этим состояниям,
мы имеем:
![]() значит, функция
значит, функция
![]() на состояниях
принимает одинаковые значения. Кроме
того, другая часть столбцов:
на состояниях
принимает одинаковые значения. Кроме
того, другая часть столбцов:
![]() такова, что
такова, что
![]() лежат в одном классе разбиения. Это
доказывает, что
неотличимы. Из таблицы автомата
теперь нетрудно получить таблицу
приведённого автомата
– для этого достаточно взять по одному
представителю в каждом классе разбиения
лежат в одном классе разбиения. Это
доказывает, что
неотличимы. Из таблицы автомата
теперь нетрудно получить таблицу
приведённого автомата
– для этого достаточно взять по одному
представителю в каждом классе разбиения
![]() Таким образом, мы получаем:
Таким образом, мы получаем:
|
|
|
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
