- •Упражнение 3.1
- •Упражнение 3.2
- •Упражнение 3.3
- •Упражнение 3.4
- •Упражнение 3.5
- •Упражнение 3.6
- •Упражнение 3.7
- •Упражнение 3.8.
- •Упражнение 3.9.
- •Упражнение 3.10.
- •Упражнение 3.14.
- •Упражнение 3.15.
- •Упражнение 3.16.
- •Упражнение 3.17.
- •Упражнение 3.18.
- •Упражнение 3.19.
- •Упражнение 3.20.
- •Управление 3.21.
- •Упражнение 3.22.
- •Упражнение 3.23.
- •Задание на 10 баллов.
Упражнение 3.1
Введите массив а в командной строке, используя квадратные скобки и разделяя элементы вектора точкой с запятой:
1)>> a = [1.3; 5.4; 6.9]
a =
1.3000
5.4000
6.9000
Введите теперь второй вектор, подавив вывод на экран:
2)>> b = [7.1; 3.5; 8.2];
3) >> s1 = [3 4 9 2]
s1 =
3 4 9 2
>> s2 = [5 3 3 2]
s2 =
5 3 3 2
Упражнение 3.2
>> v1 = [1; 2];
>> v2 = [3; 4; 5];
>> v = [v1; v2]
v =
1
2
3
4
5
Упражнение 3.3
1)>> a=[1,2;3,4]
a =
1 2
3 4
>> b=[9,8;7,6]
b =
9 8
7 6
>> c=a+b
c =
10 10
10 10
2)>> ndims(a)
ans =
2
>> size(a)
ans =
2 2
>> ndims(b)
ans =
2
>> size(b)
ans =
2 2
>> ndims(c),size(c)
ans =
2
ans =
2 2
3.1)>> s1=[1,2],s2=[3,5],s3=s1+s2
s1 =
1 2
s2 =
3 5
s3 =
4 7
3.2)>> s4=s1-s2
s4 =
-2 -3
Упражнение 3.4
1)>> v1 = [2 -3 4 1];
>> v2 = [7 5 -6 9];
>> u = v1.*v2
u =
14 -15 -24 9
2)>> p = v1.^2
p =
4 9 16 1
Упражнение 3.5
1)>> v = [4 6 8 10];
>> p = v*2
p =
8 12 16 20
>> pi = 2*v
pi =
8 12 16 20
2) >> p = v/2
p =
2 3 4 5
>> p = 2/v
??? Error using ==> mldivide
Matrix dimensions must agree.
Упражнение 3.6
1) >> v = [1.3 3.6 7.4 8.2 0.9];
>> v(4)
ans =
8.2000
2) >> v(2) = 555
v =
1.3000 555.0000 7.4000 8.2000 0.9000
3) >> u = [v(3); v(2); v(1)]
u =
7.4000
555.0000
1.3000
4) >> ind = [4 2 5];
>> w = v(ind)
w =
8.2000 555.0000 0.9000
5) >> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8];
>>w(2:6) = 0;
>> w
w =
0.1000 0 0 0 0 0 9.8000
6) >>w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8]; >> wl = w(3:5)
wl = 3.3000 5.1000 2.6000
7) >> w2 = [w(l:3) w(5:7)]
w2 = 0.1000 2.9000 3.3000 2.6000 7.1000 9.8000
8) >> gm = (u(l)*u(2)*u(3))^(l/3) gm =
17.4779
Упражнение 3.7
Создать с помощью
специальных символов вектор-строку
 и вектор-столбец
и вектор-столбец
 .
Изменить значение координаты
.
Изменить значение координаты
 на -5,значение координаты
на -5,значение координаты
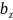 на сумму первой и второй координаты
вектора
на сумму первой и второй координаты
вектора
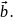 >> a=[2 4 6], b=[1;8;-2]
>> a=[2 4 6], b=[1;8;-2]
a = 2 4 6
b =
1
8
-2
>> a(2)=-5
a =
2 -5 6
>> b(3)=b(1)+b(2)
b =
1
8
9
Упражнение 3.8.
Изобразить правило треугольника.
Даны три точки с координатами A(-2 0), B(1 2), C(1 -1).
Убедиться (в тетради), что АВ+ВС=AC, здесь AB, BC и AC –векторы.
Изобразить векторы АВ и ВС синим и АС красным.
>> line([-2 1],[0 2],'Color','b')
>> line([1 1],[2 -1],'Color','b')
>> line([1 -2],[-1 0],'Color','red')
>> hold on
>> plot(1,-1,'vb','lineWidth',4)
>> plot(1,2,'>b','lineWidth',4)
>> plot(1,-1,'>r','lineWidth',4)
>> axis equal
>> grid on
>> text(-2.1,0.1,'A')
>> text(1.1,2.1,'B')
>> text(1.1,-1.1,'C')
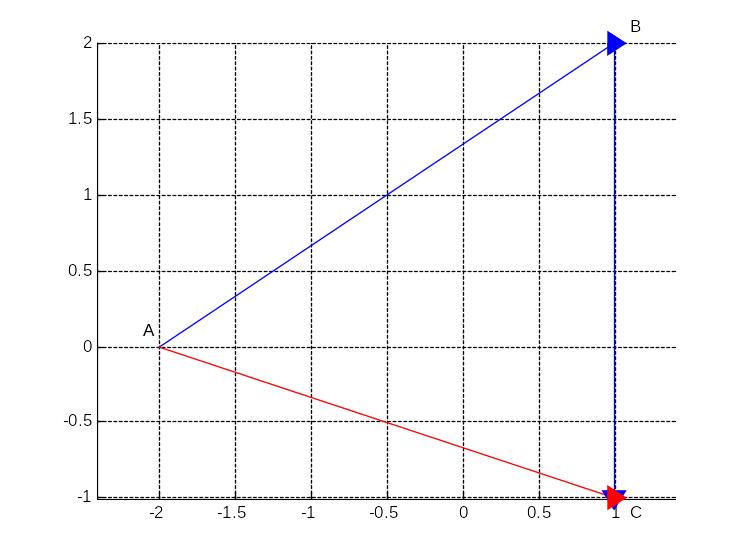
Упражнение 3.9.
Изобразить правило параллелограмма.
Дан параллелограмм ABCD, известны координаты трех его точек
A(-2 0), B(1 2), C(1 -1).
Найти координаты четвертой вершины D параллелограмма.
Показать на рисунке, что AB+ AD =AC, здесь AB, AD и AC – векторы.
Изобразить векторы АВ и AD синим и АС красным,
остальные стороны параллелограмма ВС и CD -черным.
>> line([-2 1],[0 2],'Color','b')
>> line([1 -2],[-1 0],'Color','red')
>> hold on
>> plot(1,2,'>b','lineWidth',4)
>> plot(1,-1,'>r','lineWidth',4)
>> text(-2.1,0.1,'A')
>> text(1.1,2.1,'B')
>> text(1.1,-1.1,'C')
>> a=[3,2];
>> b=[3,-1];
>> c=a+b;
>> line([-2 -2+c(1)],[0 0+c(2)],'Color','b')
>> text(4.1,1.1,'D')
>> grid on
>> line([1 1+a(1)],[-1 -1+a(2)],'Color','black')
>> line([1 1+b(1)],[2 2+b(2)],'Color','black')
>> plot(-2+c(1),0+c(2),'>b','lineWidth',4)