
- •Типовые динамические звенья
- •Математические модели типовых динамических звеньев
- •Математические модели позиционных звеньев
- •Математические модели интегрирующих звеньев
- •Математические модели дифференцирующих звеньев
- •Временные характеристики типовых динамических звеньев
- •Частотные характеристики типовых динамических звеньев
- •Интегро - дифференцирующие звенья
- •Неминимально - фазовые звенья.
- •Звено чистого запаздывания
Интегро - дифференцирующие звенья
Интегро - дифференцирующие звенья – это типовые динамические звенья, имеющие передаточные функции вида:
![]() ,
(44)
,
(44)
где
![]() - нормированные полиномы от р
первого или второго порядков. В зависимости
от вида эти полиномов и значений их
коэффициентов интегро - дифференцирующие
звенья в одних диапазонах частот имеют
интегрирующие, а в других дифференцирующие
свойства. Такие звенья широко используются
в качестве корректирующих устройств.
- нормированные полиномы от р
первого или второго порядков. В зависимости
от вида эти полиномов и значений их
коэффициентов интегро - дифференцирующие
звенья в одних диапазонах частот имеют
интегрирующие, а в других дифференцирующие
свойства. Такие звенья широко используются
в качестве корректирующих устройств.
Неминимально - фазовые звенья.
Звено называется минимально - фазовым, если все нули и полюсы его передаточной функции имеют отрицательные или равные нулю вещественные части. Звено называется неминимально - фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть. Все рассмотренные выше типовые динамические звенья являются минимально-фазовыми.
Для неминимально - фазового звена характерно, что у него сдвиг фазы по модулю больше чем у минимально-фазового звена, имеющего подобную амплитудную частотную характеристику.
К неминимально - фазовым звеньям относятся:
1. Неустойчивые звенья, передаточные функции которых имеют хоть бы один положительный полюс:
- неустойчивое апериодическое звено первого прядка с передаточной функцией
![]() ;
(45)
;
(45)
- неустойчивое апериодическое звено второго порядка с передаточной функцией
![]() ;
(46)
;
(46)
- неустойчивые колебательные звенья с передаточными функциями
![]() ;
(47)
;
(47)
![]() .
(78)
.
(78)
2. Неустойчивые звенья, у которых передаточные функции имеют положительные нули:
![]() ;
(49)
;
(49)
![]() ;
(50)
;
(50)
![]() .
(51)
.
(51)
Часть интегро - дифференцирующих звеньев, имеющих либо положительные полюсы, либо положительные нули.
4. Особые звенья, имеющие бесконечно большое число левых полюсов. К особым звеньям (неминимально - фазовым звеньям) относится звено чистого запаздывания.
Звено чистого запаздывания
Звено чистого запаздывания, как и усилительное звено, передает сигнал с входа на выход без искажения его формы. Однако все мгновенные значения входного сигнала выходная переменная принимает с некоторым отставанием (запаздыванием). Способностью задерживать сигнал во времени, не изменяя его формы, обладают многие элементы промышленных систем автоматизации. К ним относятся, в первую очередь, транспортные средства (конвейеры, транспортеры, трубопроводы), а так же некоторые технологические агрегаты.
Уравнение звена чистого запаздывания имеет вид:
![]() ,
(52)
,
(52)
где
![]() - величина чистого запаздывания
(длительность запаздывания). Уравнение
(52) не является дифференциальным
уравнением, а относится к классу особых
уравнений со смещенным (запаздывающим)
аргументом. Оно показывает, что выходной
сигнал y(t)
повторяет все изменения входного
сигнала x(t),
но с отставанием на время
.
- величина чистого запаздывания
(длительность запаздывания). Уравнение
(52) не является дифференциальным
уравнением, а относится к классу особых
уравнений со смещенным (запаздывающим)
аргументом. Оно показывает, что выходной
сигнал y(t)
повторяет все изменения входного
сигнала x(t),
но с отставанием на время
.
Передаточная функция звена чистого запаздывания в соответствии с теоремой запаздывания преобразования Лапласа имеет вид:
![]() .
(53)
.
(53)
Переходная и весовая функции звена чистого запаздывания определяются соотношениями:
![]() ;
(54)
;
(54)
![]() .
(55)
.
(55)
Переходная и весовая характеристики звена чистого запаздывания приведены на рис. 13.
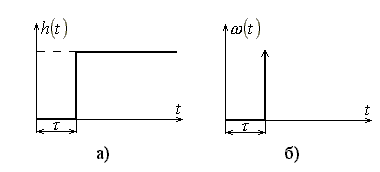
Рис. 13. Переходная и весовая характеристики звена чистого запаздывания.
Частотная передаточная функция звена чистого запаздывания, получается на основе передаточной функции (82) и имеет вид:
![]() .
(56)
.
(56)
Амплитудно-фазовая частотная характеристика звена чистого запаздывания представлена на рис. 14 и является окружностью единичного радиуса с центром в начале координат.
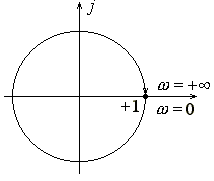
Рис. 14. Амплитудно-фазовая частотная характеристика звена чистого запаздывания.
Частотные характеристики звена чистого запаздывания, полученные на основе частотной передаточной функции (85) имеют вид:
![]() (57)
(57)
![]() .
(58)
.
(58)
Амплитудная и фазовая частотные характеристики звена чистого запаздывания приведены на рис. 15;
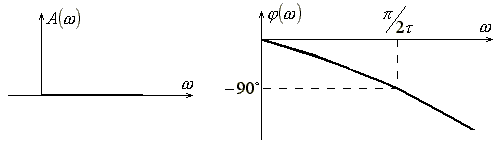
Рис. 15 Амплитудная и фазовая частотные характеристики звена чистого запаздывания
ЛАЧХ и ЛФЧХ звена чистого запаздывания приведены на рис. 16,
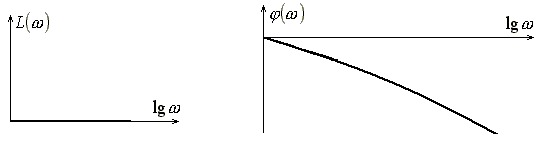
Рис. 16. ЛАЧХ и ЛФЧХ звена чистого запаздывания
где
![]() Звено
чистого запаздывания в большинстве
случаев ухудшает устойчивость САУ и
делает их трудно управляемыми.
Звено
чистого запаздывания в большинстве
случаев ухудшает устойчивость САУ и
делает их трудно управляемыми.
