Математические модели интегрирующих звеньев

1. Идеальное интегрирующее звено описывается дифференциальным уравнением

(14)

и передаточной функцией

, (15)

которое характеризуется только одним параметром k.

Все интегрирующие звенья являются астатическими в отличие от позиционных, являющихся статическими. Идеальное интегрирующее звено – элементарное звено, входящее в состав всех остальных интегрирующих звеньев.

2. Реальное интегрирующее звено описывается дифференциальным уравнением

(16)

и передаточной функцией

. (17)

Реальное интегрирующее звено – составное звено, представляющее собой последовательное соединение идеального интегрирующего звена и апериодического звена первого порядка (рис. 2), так как

 

Рис. 2. Структурная схема реального интегрирующего звена

, (18)

где k=k₁k₂. Реальное интегрирующее звено характеризуется двумя параметрами: k и T.

3. Изодромное звено первого порядка описывается дифференциальным уравнением

(19)

и передаточной функцией

. (20)

Изодромное звено первого порядка – составное звено, представляющее собой параллельное соединение усилительного звена и идеального интегрирующего звена

(рис. 3),

Рис. 3. Структурная схема изодромного звена первого порядка.

так как

(21)

и характеризуется двумя параметрами k и T.

4. Изодромное звено второго порядка описывается дифференциальным уравнением

, (22)

и передаточной функцией

. (23)

Изодромное звено второго порядка – составное звено, представляющее собой параллельно – последовательное соединение усилительного звена и идеальных интегрирующих звеньев (рис. 4), так как

, (24)

где и характеризуется тремя параметрами .

Рис. 4. Структурная схема изодромного звена второго порядка

Математические модели дифференцирующих звеньев

1. Идеальное дифференцирующее звено описывается дифференциальным уравнением

(25)

и передаточной функцией

. (26)

Идеальное дифференцирующее звено - элементарное звено, входящее в состав всех дифференцирующих звеньев и характеризуется только параметром .

2. Реальное дифференцирующее звено описывается дифференциальным уравнением

(27)

и передаточной функцией

. (28)

Реальное дифференцирующее звено – составное звено, представляющее собой последовательное соединение идеального дифференцирующего звена и апериодического звена первого порядка (рис. 5), так как

, (29)

где и характеризуется двумя параметрами: k и T.

Рис. 5. Структурная схема реального дифференцирующего звена

3. Форсирующее звено первого порядка описывается дифференциальным уравнением

(30)

и передаточной функцией

. (31)

Форсирующее звено первого порядка – составное звено, представляющее собой параллельное соединение усилительного звена и идеального дифференцирующего звена (рис. 6), так как

Рис. 6 Структурная схема форсирующего звена первого порядка

, (32)

где и характеризуется двумя параметрами: k и T.

4. Форсирующее звено второго порядка описывается дифференциальным уравнением

(33)

и передаточной функцией

, (34)

где .

Форсирующее звено второго порядка – составное звено, представляющее собой параллельно - последовательное соединение усилительного звена и идеальных дифференцирующих звеньев (рис. 7) , так как

, (35)

где и характеризуется тремя переменными: .

 

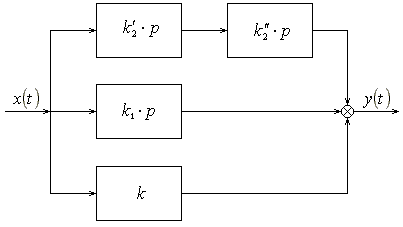
Рис. 7. Структурная схема форсирующего звена второго порядка