Модуль № 1
Опрацювання лекцій № 1, 3, 4, 6, 7, 9, 10 – 12.
Підготовка до самостійної роботи № 1.
Підготовка до самостійної роботи № 2.
Підготовка до заліку за теорією.
Підготовка до обов’язкової контрольної роботи.
Виконання першої частини семестрового завдання.
Опрацювання лекцій № 1, 3, 4, 6, 7, 9, 10 - 12.
При опрацьовуванні лекції необхідно прочитати її, вивчити основні визначення, терміни і формули, відповісти на контрольні питання, які є після кожної лекції. Якщо виникли питання, то більш детально розібрати тему по літературі, яка вказана в даній методиці, або звернутися за консультацією до викладача.
[1]
Підготовка до самостійної роботи № 1.
Для якісної підготовки до самостійної роботи № 1 необхідно розв’язати такі задачі:
1)
Знайти добуток матриць
,
якщо:
.
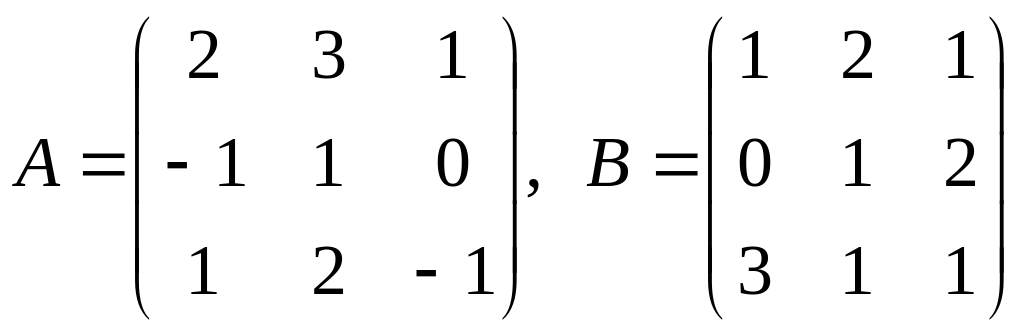2) Знайти визначники другого порядку:
А)
;
Б)
.
3) Обчислити визначник третього порядку двома способами – за правилом трикутника та розкладанням по третьому рядку та другому стовпцю:
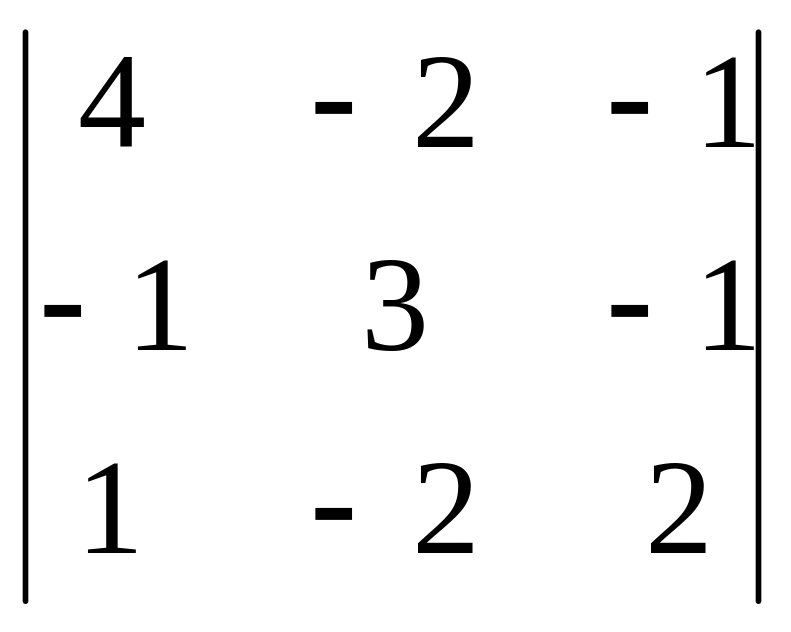
4) Обчислити визначник третього порядку двома способами – за правилом трикутника та розкладанням по другому рядку та першому стовпцю:
Відповіді:
1)
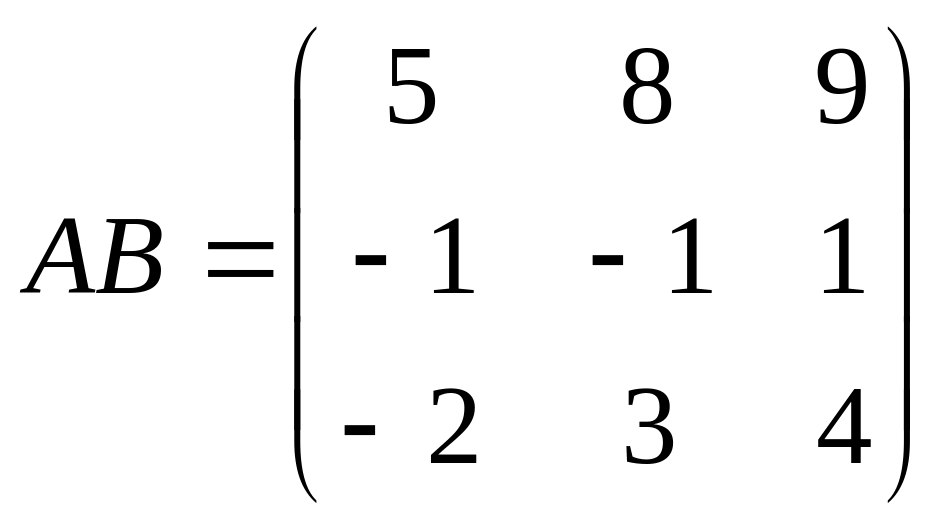2)
А) 18;
Б) -3 3)
15 4)
125.
Підготовка до самостійної роботи № 2.
Для якісної підготовки до самостійної роботи № 1 необхідно розв’язати такі задачі:
1)
Знайти скалярний добуток векторів
і
і кут між ними, якщо
,
,
,
.
2)
Знайти площу трикутника
,
якщо
,
,
.
3) Встановити, чи компланарні вектори:
А)
; Б)
Відповіді:
1)
2)
3) А) компланарні; Б) не компланарні
4. Підготовка до заліку за теорією
Залік за модулем містить чотири теоретичні питання по лекціям даної теми. Для підготовки до заліку за теорією необхідно підготувати наступні питання:
Визначення матриці.
Види матриць: квадратна (порядок, діагоналі), діагональна, одинична, вектори.
Дії над матрицями: додавання, множення на число, транспонування.
Дії над матрицями: добуток двох матриць.
Визначник другого порядку. Обчислення визначника третього порядку за правилом трикутника.
Властивості визначника.
Мінор, алгебраїчне доповнення, теорема про розкладання визначника по рядку (стовпцю).
Системи лінійних рівнянь: розв’язок системи, сумісна, несумісна, визначена, невизначена система, розширена матриця.
Метод Крамера (розглянути випадки, коли визначник системи дорівнює нулю).
Метод Гауса (еквівалентні системи, елементарні перетворення, прямий та зворотній хід).
Вироджена, невироджена матриці, обернена матриця, матрична форма системи лінійних рівнянь, вивід формули матричного методу.
Алгоритм знаходження оберненої матриці.
Алгоритм матричного методу.
Визначення вектору, довжини вектору, нульового вектору, орту, розкладання вектору по одиничним векторам.
Координати вектору, колінеарність векторів, умова колінеарності векторів.
Довжина вектору, координати середини вектору.
Скалярний добуток, кут між векторами.
Скалярний добуток, його властивості.
Визначення векторного добутку та його властивості.
Обчислення векторного добутку та його геометричний зміст.
Визначення і обчислення мішаного добутку трьох векторів.
Компланарність векторів. Геометричний зміст мішаного добутку.
5. Підготовка до обов’язкової контрольної роботи.
Для підготовки до контрольної роботи необхідно розв’язати наступні задачі:
1) Розв’язати систему рівнянь матричним способом, зробити перевірку:
2) Знайти площу
паралелограма, побудованого на векторах
,
.
3) Дано вершини тетраедра А(1, 1, 1), В(3, 7, 2), С(3, -3, -3), D(2, -2, 0). Обчислити об’єм тетраедра та довжину ребра АВ.
Відповіді:
1) (0;
0; -2) 2)
3)
5;
6. Виконання першої частини семестрового завдання.
Правила оформлення семестрового завдання дані у вступі даного методичного посібника. Згідно свого варіанту виконайте завдання першої частини, які вказані на сторінці .