2. Уравнения вида

Это уравнение является частным случаем уравнения (1) при

Процедура, описанная в разд. 5.1, приводит к уравнениям

(5)

Здесь вместо второго уравнения системы (4) использовано исходное уравнение (так можно делать поскольку первое уравнение системы не зависит от у).

Интегрируя первое уравнение (5), получим решение в параметрическом виде

2. Уравнения вида

Это уравнение является частным случаем уравнения (1) при

Процедура, описанная в разд. 5.1, приводит к уравнениям

(6)

Здесь вместо первого уравнения системы (4) использовано исходное уравнение (так можно делать п

оскольку второе уравнение системы не зависит от х).

Интегрируя второе уравнение (6), получим решение в параметрическом виде

2. Уравнение Клеро

Уравнение Клеро является частным случаем уравнения (1) при

и может быть записано в виде

(7)

Заменяя в равенстве величины и их значениями из (7), приходим к уравнению

Которое распадается на два уравнения: dt = 0 и Решение первого очевидно: t = C. Оно дает общее решение уравнения Клеро

(8)

Представляющее собой семейство прямых. Второе уравнение дает решение в параметрической форме

Которое является особым и представляет собой огибающую семейства прямых (8).

5.5 Уравнение Лагранжа

Уравнение Лагранжа является частным случаем уравнения (1) при

. В частном случае оно совпадает с уравнением Клеро (см. разд. 5.4). Процедура, описанная в разд. 5.1, приводит к уравнениям

(9)

Здесь вместо второго уравнения системы (4) использовано исходное уравнение (так можно делать поскольку первое уравнение системы не зависит от у).

Первое уравнение системы (9) является линейным. Его общее решение имеет вид

(функция и определяются по формулам из разд. 2.5). Подставляя это выражение во второе равенство (9), находим общее решение уравнения Лагранжа в параметрической форме

Замечание 3. Данный метод может привести к потере решений вида где t_k – корни уравнения f(t) – t = 0. Эти решения могут быть как частными, так и особыми.

6. Приближенные аналитические методы решения уравнений

6.1 Метод последовательных приближений (метод Пикара)

Метод последовательных приближений состоит из двух этапов. На первом этапе

задача Коши

(уравнение), (1)

(начальное условие) (2)

сводится к эквивалентному интегральному уравнению

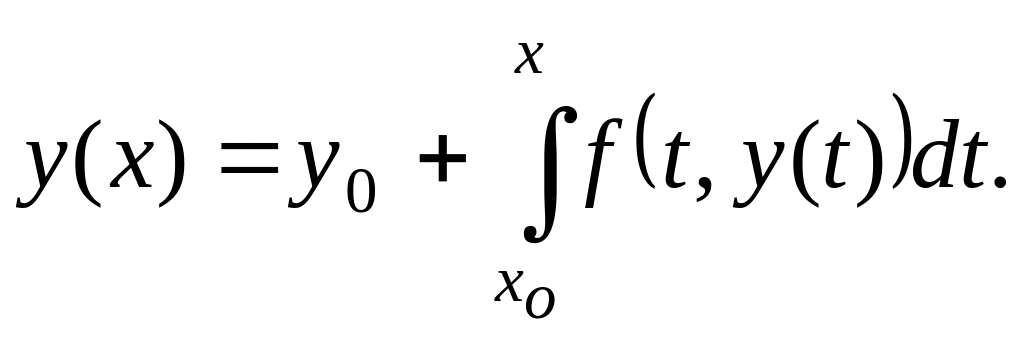(3)

Затем решение уравнения (3) ищется с помощью последовательных приближений по формуле

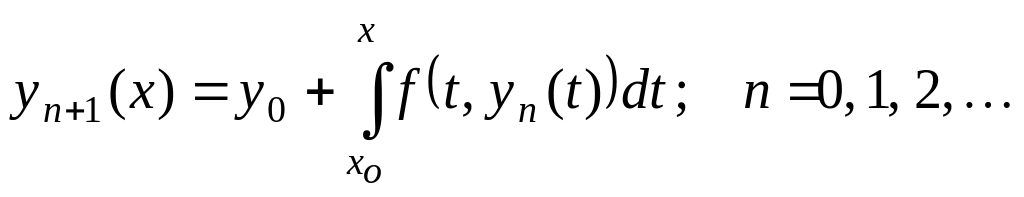
Выбор начального приближения безразличен; проще всего за начальное приближение взять число . Указанный процесс сходится при , если выполнены условия теорем из разд. 1.2.