2. Уравнения, не разрешенные относительно производной.

В общем случае уравнения, не разрешенные относительно производной, имеют вид

(3)

• Теорема существования и единственности. Существует единственное

решение у = у (х) уравнения (3), удовлетворяющее условиям и , где - один из действительных корней уравнения если в некоторой окрестности точки выполнены условия:

1. Функция 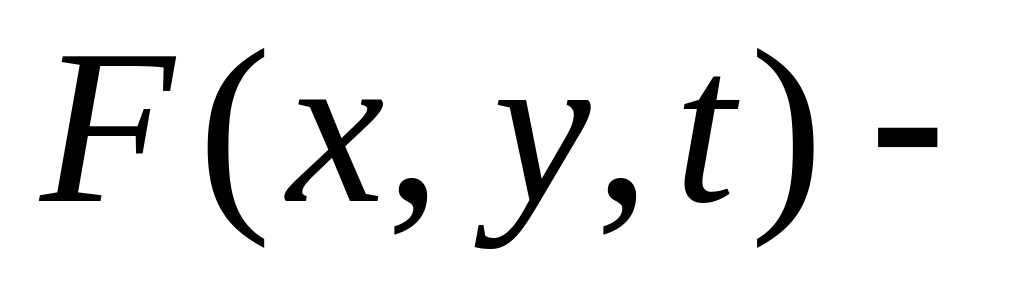непрерывна по всем трем аргументам;

2. Частная производная F_t существует и отлична от нуля;

3. Существует ограниченная по модулю частная производная F_y:

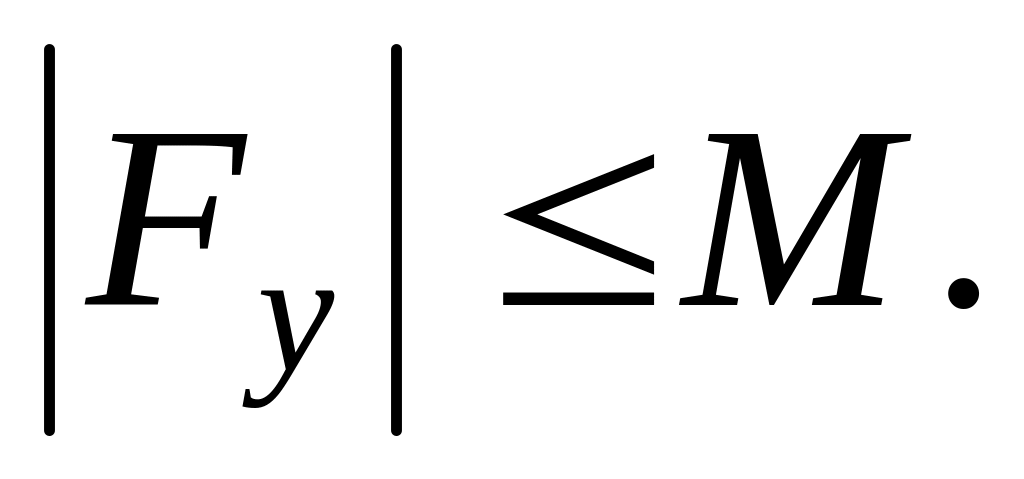
Указанное решение существует при , где > 0 – некоторое (достаточно малое) число.

2. Особые решения

• Точки (х, у), в которых нарушается единственность решений уравнения (3),

называются особыми. Если удовлетворяются условия 1) и 3) теоремы существования и единственности, то в особых точках должны одновременно выполняться равенства

(4)

которые представляют собой параметрическую запись t – дискриминантной кривой. Исключая из (4) параметр t, в ряде случаев можно получить уравнение этой кривой в неявном виде Если какая-нибудь ветвь кривой состоит из особых точек и одновременно является интегральной кривой, то она называется особой интегральной кривой, а функция – особым решением уравнения (3).

• Особые решения можно найти путем определения огибающей семейства

интегральных кривых уравнения (3). Огибающая входит в состав С -дискриминантной кривой, которая задается уравнениями .

Некоторая ветвь С - дискриминантной кривой будет огибающей, если на ней:

1. существуют ограниченные по модулю частные производные:

2. 

2. Уравнения, разрешенные относительно производной. Простейшие методы

интегрирования

2.1 Уравнения с разделенными и разделяющимися переменными

• Уравнения с разделенными переменными имеют вид

Эквивалентная запись уравнения: (правая часть уравнения зависит только от х, а левая – только от у). Общее решение получается почленным интегрированием:

где С – произвольная постоянная.

П р и м е р 1. Решить уравнение .

Записав уравнение в виде и представив это как , интегрируя имеем

или у = С/х. Решением является также у = 0.

• Уравнения с разделяющимися переменными имеют вид

Делим обе части на В результате приходим к уравнению с разделенными переменными. После интегрирования получим

Замечание. При почленном делении уравнения на могут быть потеряны решения, обращающие функцию в нуль, а также решение вида х = а , где .

П р и м е р 2. Проинтегрировать уравнение .

Разделяем переменные Интегрируя находим Откуда

При делении на могли быть потеряны решения