
Преобразования
Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и и продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны). Изогонально сопряжёнными являются многие пары замечательных точек: центр описанной окружности и ортоцентр, центроид и точка Лемуана, точки Брокара. Точки Аполлония изогонально сопряжены точкам Торричелли, а центр вписанной окружности изогонально сопряжён сам себе. Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники — в прямые. Так, изогонально сопряжены гипербола Киперта и ось Брокара, гипербола Енжабека и прямая Эйлера, гипербола Фейербаха и линия центров вписанной о описанной окружностей. Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают. Фокусы вписанных эллипсов изогонально сопряжены.
Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением. Оно также переводит прямые в описанные коники.Изотомически сопряжены точки Жергонна и Нагеля. При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в 00510000510010400010000180118000181%22http://ru.wikipedia.org/w/index.php?title=%D0%91%D0%B5%D1%81%D0%BA%D0%BE%D0%BD%D0%B5%D1%87%D0%BD%D0%BE_%D1%83%D0%B4%D0%B0%D0%BB%D1%91%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BF%D1%80%D1%8F%D0%BC%D0%B0%D1%8F&action=edit&redlink=1"удалённуюпрямую"бесконечно HYPERLINK "%22бесконечно%20HYPERLINK%20%22http://ru.wikipedia.org/w/index.php?title=%D0%91%D0%B5%D1%81%D0%BA%D0%BE%D0%BD%D0%B5%D1%87%D0%BD%D0%BE_%D1%83%D0%B4%D0%B0%D0%BB%D1%91%D0%BD%D0%BD%D0%B0%D1%8F_%D0%BF%D1%80%D1%8F%D0%BC%D0%B0%D1%8F&action=edit&redlink=1"удалённуюпрямую"удалённуюпрямуюперейдёт описанный эллипс Штейнера.
Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием. Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция — 09100501080200050105001100070020000805проективное преобразование, которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.
Если
продолжить стороны чевианного треугольника
некоторой точки и взять их точки
пересечения с соответствующими сторонами,
то полученные точки пересечения будут
лежать на одной прямой, называемой трилинейной
полярой исходной
точки. Ортоцентрическая ось —
трилинейная поляра ортоцентра; трилинейной
полярой центра вписанной окружности
служит ось внешних биссектрис. Трилинейные
поляры точек, лежищих на описанной
конике, пересекаются в одной точке (для
описанной окружности это точка Лемуана,
для описанного эллипса Штейнера —
центроид). Композиция изогонального
(или изотомического) сопряжения и
трилинейной поляры является преобразованием
двойственности (если точка, изогонально
(изотомически) сопряжённая точке  ,
лежит на трилинейной поляре точки
,
лежит на трилинейной поляре точки  ,
то трилинейная поляра точки, изогонально
(изотомически) сопряжённой точке
лежит
на трилинейной поляре точки
).
,
то трилинейная поляра точки, изогонально
(изотомически) сопряжённой точке
лежит
на трилинейной поляре точки
).
Кубики
Кубика —
это кривая третьего порядка (задающаяся
уравнением третьей степени). Многие
замечательные кубики, связанные с
треугольником, строятся следующим
образом: фиксируется точка в плоскости
(возможно бесконечно удалённая). Тогда
множество таких точек
,
что прямая  проходит
через эту точку, является описанной
около треугольника кубикой (здесь
проходит
через эту точку, является описанной
около треугольника кубикой (здесь 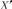 —
точка, изогонально сопряжённая
).
Такие кубики проходят также через центры
вписанной и вневписанных окружностей,
а также через саму фиксированную точку
и изогонально сопряжённую
ей.0210510300180080%5B10%5D"[HYPERLINK
"%BA%22%5B10%5D"10HYPERLINK
"%BA%22%5B10%5D"]
—
точка, изогонально сопряжённая
).
Такие кубики проходят также через центры
вписанной и вневписанных окружностей,
а также через саму фиксированную точку
и изогонально сопряжённую
ей.0210510300180080%5B10%5D"[HYPERLINK
"%BA%22%5B10%5D"10HYPERLINK
"%BA%22%5B10%5D"]
Кубика Дарбу получается, если зафиксировать точку, симметричную ортоцентру относительно центра описанной окружности. Она проходит через ортоцентр и центр описанной окружности.
Кубика Томсона получается, если в качестве фиксированной точки выбрать центроид. Кубика Томсона проходит через центроид, точку Лемуана, ортоцентр, центр описанной окружности, середины сторон и середины высот.
Кубика Мак-Кэя получится, если в качестве фиксированной точки взять центр описанной окружности. Она также проходит через ортоцентр и центр описанной окружности.
Кубика Нейберга — множество таких точек , что
 —
прямой Эйлера (зафиксирована её
бесконечно удалённая точка). На этой
кубике лежит более 15 замечательных
точек, в частности, точки Торричелли,
Аполлония, ортоцентр, центр описанной
окружности, вершины правильных
треугольников, построенных на сторонах
(внешним или внутренним образом), точки,
симметричные вершинам относительно
сторон, а также лежащие на всех кубиках
центры вписанной и вневписанных
окружностей.
—
прямой Эйлера (зафиксирована её
бесконечно удалённая точка). На этой
кубике лежит более 15 замечательных
точек, в частности, точки Торричелли,
Аполлония, ортоцентр, центр описанной
окружности, вершины правильных
треугольников, построенных на сторонах
(внешним или внутренним образом), точки,
симметричные вершинам относительно
сторон, а также лежащие на всех кубиках
центры вписанной и вневписанных
окружностей.
Соотношения в треугольнике
Примечание: в
данном разделе  ,
,  ,
,  —
это длины трёх сторон треугольника,
и
—
это длины трёх сторон треугольника,
и  ,
, 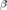 ,
,  —
это углы, лежащие соответственно напротив
этих трёх сторон (противолежащие углы).
—
это углы, лежащие соответственно напротив
этих трёх сторон (противолежащие углы).
Неравенство треугольника
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:
 ;
;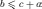 ;
; .
.
Неравенство треугольника является одной из аксиом 09051108000метрики.
Теорема о сумме углов треугольника

Теорема синусов
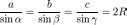 ,
,
где R — радиус окружности, описанной вокруг треугольника. Из теоремы следует, что если a < b < c, то α < β < γ.
Теорема косинусов

Является обобщением 020501050000908100030100теоремы Пифагора.
[0210510300180080%22править"править]020501050001000030501002Теорема тангенсов
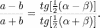
Другое название: формула Региомонтана.
Прочие соотношения
Метрические
соотношения в треугольнике приведены
для  :
:


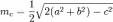

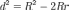 — 04010100000900510004018110510300180080001формула
Эйлера
— 04010100000900510004018110510300180080001формула
Эйлера
Где:
 —
отрезки,
на которые 008110501108100биссектриса
—
отрезки,
на которые 008110501108100биссектриса  делит
сторону
,
делит
сторону
, — 090504080000011051030018008000медианы,
проведённые соответственно к
сторонам
,
и
,
— 090504080000011051030018008000медианы,
проведённые соответственно к
сторонам
,
и
, — 0181010011051030018008000высоты,
опущенные соответственно на
стороны
,
и
,
— 0181010011051030018008000высоты,
опущенные соответственно на
стороны
,
и
, — 0000040811%22радиус"радиус 0008100000018001106001118вписанной
окружности,
— 0000040811%22радиус"радиус 0008100000018001106001118вписанной
окружности, — 0000040811%22радиус"радиус 09008100000018001106001118описанной
окружности,
— 0000040811%22радиус"радиус 09008100000018001106001118описанной
окружности, —
полупериметр,
—
полупериметр, — 0900100041803050005110818площадь,
— 0900100041803050005110818площадь, —
расстояние
между центрами вписанной и описанной
окружностей.
—
расстояние
между центрами вписанной и описанной
окружностей.
Решение треугольников
Основная статья: 000510500805110510300180080002Решение треугольников
Вычисление неизвестных сторон и углов треугольника, исходя из известных, исторически получило название 000510500805110510300180080002«решения треугольников». При этом используются приведенные выше общие тригонометрические теоремы.
Площадь треугольника
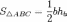 ,
так как
,
так как 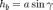 ,
то:
,
то:
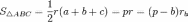
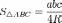
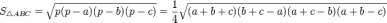 — 04010100000510000формула
Герона
— 04010100000510000формула
Герона
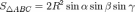
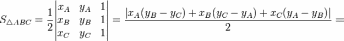

 —
для 0911800103001801809110510300180080прямоугольного
треугольника
—
для 0911800103001801809110510300180080прямоугольного
треугольника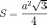 —
для 0000020011010000809110510300180080равностороннего
треугольника
—
для 0000020011010000809110510300180080равностороннего
треугольника —
если
треугольник задан по стороне и двум
прилежащим к ней углам
—
если
треугольник задан по стороне и двум
прилежащим к ней углам —
если
треугольник задан по стороне и двум
прилежащим к ней углам (аналогично
формуле 6!)
—
если
треугольник задан по стороне и двум
прилежащим к ней углам (аналогично
формуле 6!) —
ориентированная
площадь треугольника на комплексной
плоскости с вершинами в a, b, c.
—
ориентированная
площадь треугольника на комплексной
плоскости с вершинами в a, b, c.
Где:
 —
высота,
проведённая на сторону
,
—
высота,
проведённая на сторону
,— полупериметр,
— радиус 0008100000018001106001118вписанной окружности,
 —
радиус 000502008100000018001106001118вневписанной
окружности,
касающейся стороны
,
—
радиус 000502008100000018001106001118вневписанной
окружности,
касающейся стороны
,— радиус 09008100000018001106001118описанной окружности,
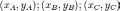 —
координаты
вершин треугольника.
—
координаты
вершин треугольника.
Для площади справедливы неравенства:
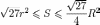 ,
причём оба равенства достигаются.
,
причём оба равенства достигаются.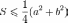 ,
где равенство достигается для
равнобедренного прямоугольного
треугольника.
,
где равенство достигается для
равнобедренного прямоугольного
треугольника.
Вычисление площади треугольника в пространстве с помощью векторов
Пусть
вершины треугольника находятся в
точках 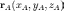 ,
,  ,
,  .
.
Введём
вектор площади 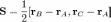 .
Длина этого вектора равна площади
треугольника, а направлен он по нормали
к плоскости треугольника:
.
Длина этого вектора равна площади
треугольника, а направлен он по нормали
к плоскости треугольника:

Положим 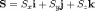 ,
где
,
где 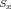 ,
, 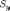 ,
,  —
проекции треугольника на координатные
плоскости. При этом
—
проекции треугольника на координатные
плоскости. При этом
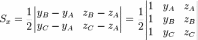
и аналогично
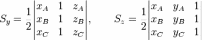
Площадь
треугольника равна  .
.
Альтернативой служит вычисление длин сторон (по 020501050000908100030100теореме Пифагора) и далее по 04010100000510000формуле Герона.
Теоремы о треугольниках
Теорема HYPERLINK "http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%94%D0%B5%D0%B7%D0%B0%D1%80%D0%B3%D0%B0"Дезарга: если два треугольника перспективны (прямые, проходящие через соответственные вершины треугольников, пересекаются в одной точке), то их соответственные стороны пересекаются на одной прямой.
Теорема HYPERLINK "http://ru.wikipedia.org/w/index.php?title=%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A1%D0%BE%D0%BD%D0%B4%D0%B0&action=edit&redlink=1"Сонда́: если два треугольника перспективны и ортологичны (перпендикуляры, опущенные из вершин одного треугольника на стороны, противоположные соответственным вершинам треугольника, и наоборот), то оба центра ортологии (точки пересечения этих перпендикуляров) и центр перспективы лежат на одной прямой, перпендикулярной оси перспективы (прямой из теоремы Дезарга).
История изучения
Свойства треугольника, изучающиеся в школе, за редким исключением, известны с античности.
Теорема HYPERLINK "http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A7%D0%B5%D0%B2%D1%8B"Чевы была доказана в 02050XI веке арабским учёным 011100018091100000008010051041%22http://ru.wikipedia.org/w/index.php?title=%D0%AE%D1%81%D1%83%D1%84_%D0%B0%D0%BB%D1%8C-%D0%9C%D1%83%D1%82%D0%B0%D0%BC%D0%B0%D0%BD_%D0%B8%D0%B1%D0%BD_%D0%A5%D1%83%D0%B4&action=edit&redlink=1"аль-МутаманомHYPERLINK "http://ru.wikipedia.org/w/index.php?title=%D0%AE%D1%81%D1%83%D1%84_%D0%B0%D0%BB%D1%8C-%D0%9C%D1%83%D1%82%D0%B0%D0%BC%D0%B0%D0%BD_%D0%B8%D0%B1%D0%BD_%D0%A5%D1%83%D0%B4&action=edit&redlink=1" ибнХудом"Юсуфом HYPERLINK "%22Юсуфом%20HYPERLINK%20%22http://ru.wikipedia.org/w/index.php?title=%D0%AE%D1%81%D1%83%D1%84_%D0%B0%D0%BB%D1%8C-%D0%9C%D1%83%D1%82%D0%B0%D0%BC%D0%B0%D0%BD_%D0%B8%D0%B1%D0%BD_%D0%A5%D1%83%D0%B4&action=edit&redlink=1"аль-МутаманомHYPERLINK "http://ru.wikipedia.org/w/index.php?title=%D0%AE%D1%81%D1%83%D1%84_%D0%B0%D0%BB%D1%8C-%D0%9C%D1%83%D1%82%D0%B0%D0%BC%D0%B0%D0%BD_%D0%B8%D0%B1%D0%BD_%D0%A5%D1%83%D0%B4&action=edit&redlink=1" ибнХудом"аль-МутаманомHYPERLINK "%22Юсуфом%20HYPERLINK%20%22http://ru.wikipedia.org/w/index.php?title=%D0%AE%D1%81%D1%83%D1%84_%D0%B0%D0%BB%D1%8C-%D0%9C%D1%83%D1%82%D0%B0%D0%BC%D0%B0%D0%BD_%D0%B8%D0%B1%D0%BD_%D0%A5%D1%83%D0%B4&action=edit&redlink=1"аль-МутаманомHYPERLINK "http://ru.wikipedia.org/w/index.php?title=%D0%AE%D1%81%D1%83%D1%84_%D0%B0%D0%BB%D1%8C-%D0%9C%D1%83%D1%82%D0%B0%D0%BC%D0%B0%D0%BD_%D0%B8%D0%B1%D0%BD_%D0%A5%D1%83%D0%B4&action=edit&redlink=1" ибнХудом" ибн Худом, однако его доказательство было забыто. Она была доказана вновь итальянским математиком 07050200006002000008%22http://ru.wikipedia.org/wiki/%D0%A7%D0%B5%D0%B2%D0%B0,_%D0%94%D0%B6%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%B8%22Чевой"Джованни HYPERLINK "%22Джованни%20HYPERLINK%20%22http://ru.wikipedia.org/wiki/%D0%A7%D0%B5%D0%B2%D0%B0,_%D0%94%D0%B6%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%B8%22Чевой"Чевой в 03004%20году"1678 HYPERLINK "%221678%20году"году.
Дальнейшее изучение треугольника началось в 02050XVII веке: была доказана 02050105000005070010300%22http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%94%D0%B5%D0%B7%D0%B0%D1%80%D0%B3%D0%B0%22Дезарга"теорема HYPERLINK "%22теорема%20HYPERLINK%20%22http://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%94%D0%B5%D0%B7%D0%B0%D1%80%D0%B3%D0%B0%22Дезарга"Дезарга (1636), открыты некоторые свойства точки Торричелли (1659). В 02050XVIII веке была обнаружена 0911800018009005100прямая Эйлера и 090110600111804050218108101050окружность шести точек (1765). В 03004%20году"1828 HYPERLINK "%221828%20году"году была доказана 020501050000405090510100100теорема Фейербаха. В начале 02050XIX века была открыта 020100000510300000точка Жергонна.
Многие факты, связанные с треугольником, были открыты в конце 02050XIX века. К этому времени относится творчество 09050100000080181%22http://ru.wikipedia.org/w/index.php?title=%D0%9B%D0%B5%D0%BC%D1%83%D0%B0%D0%BD,_%D0%AD%D0%BC%D0%B8%D0%BB%D1%8C&action=edit&redlink=1"Лемуана"Эмиля HYPERLINK "%22Эмиля%20HYPERLINK%20%22http://ru.wikipedia.org/w/index.php?title=%D0%9B%D0%B5%D0%BC%D1%83%D0%B0%D0%BD,_%D0%AD%D0%BC%D0%B8%D0%BB%D1%8C&action=edit&redlink=1"Лемуана"Лемуана, 0100001001081%22http://ru.wikipedia.org/w/index.php?title=%D0%91%D1%80%D0%BE%D0%BA%D0%B0%D1%80,_%D0%90%D0%BD%D1%80%D0%B8&action=edit&redlink=1"Брокара"Анри HYPERLINK "%22Анри%20HYPERLINK%20%22http://ru.wikipedia.org/w/index.php?title=%D0%91%D1%80%D0%BE%D0%BA%D0%B0%D1%80,_%D0%90%D0%BD%D1%80%D0%B8&action=edit&redlink=1"Брокара"Брокара, Жозефа Нейберга, 0100040009180511Пьера HYPERLINK "%22Пьера%20Сонда́"Сонда́.
Мистика связанная с треугольником:
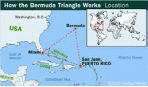
Бермудский треугольник — район в Атлантическом океане, в котором якобы происходят таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы.
Выдвигаются различные гипотезы для объяснения этих исчезновений, от необычных погодных явлений до похищений инопланетянами.
Исчезновение пяти самолетов-торпедоносцев "Эвенджер" (Мститель) 5 декабря 1945 года до сих пор остается едва ли не самой громкой катастрофой, случившейся в этом районе Атлантического океана. Именно после этого события истории о "треугольнике смерти" начали проникать в печать.
