
Эллипсы, параболы и гиперболы

Вписанная коника (эллипс) и её перспектор
В треугольник можно вписать бесконечно много коник (0000801%22эллипсов"эллипсов, 0900100010000парабол или 0080051010000000105000108000гипербол). Если в треугольник вписать произвольную конику и соединить точки касания с противоположными вершинами, то получившиеся прямые пересекутся в одной точке, называемой перспектором коники. Для любой точки плоскости, не лежащей на стороне или на её продолжении существует вписанная коника с перспектором в этой точке.0210510300180080%5B1%5D"[HYPERLINK "%BA%22%5B1%5D"1HYPERLINK "%BA%22%5B1%5D"]

Описанный эллипс Штейнера и чевианы, проходящие через его фокусы
В треугольник можно вписать эллипс, который касается сторон в серединах. Такой эллипс называется вписанным эллипсом Штейнера (его перспектором будет центроид треугольника).0210510300180080%5B2%5D"[HYPERLINK "%BA%22%5B2%5D"2HYPERLINK "%BA%22%5B2%5D"] Описанный эллипс, который касается прямых, проходящих через вершины параллельно сторонам, называется описанным эллипсом Штейнера. Если 01108000050105001100070020000805аффинным преобразованием («перекосом») перевести треугольник в правильный, то его вписанный и описанный эллипс Штейнера перейдут во вписанную и описанную окружности. Чевианы, проведённые через фокусы описанного эллипса Штейнера (точки Скутина), равны (теорема Скутина). Изо всех описанных эллипсов описанный эллипс Штейнера имеет наименьшую площадь, а изо всех вписанных наибольшую площадь имеет вписанный эллипс Штейнера.0210510300180080%5B3%5D"[HYPERLINK "%BA%22%5B3%5D"3HYPERLINK "%BA%22%5B3%5D"]

Эллипс Брокара и его перспектор — точка Лемуана
Эллипс с фокусами в точках Брокара называется эллипсом Брокара. Его перспектором служит точка Лемуана.

Свойства вписанной параболы

Парабола Киперта
Перспекторы вписанных парабол лежат на описанном эллипсе Штейнера. Фокус вписанной параболы лежит на описанной окружности, а директриса проходит через ортоцентр. Парабола, вписанная в треугольник, имеющая директрисой прямую Эйлера, называется параболой Киперта. Её перспектор — четвёртая точка пересечения описанной окружности и описанного эллипса Штейнера, называемая точкой Штейнера.
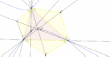
Гипербола Киперта
Если описанная гипербола проходит через точку пересечения высот, то она равносторонняя (то есть её асимптоты перпендикулярны). Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек.
Гипербола Киперта — описанная гипербола, проходящая через центроид и ортоцентр. Если на сторонах треугольника построить подобные равнобедренные треугольники (наружу или внутрь), а затем соединить их вершины с противоположными вершинами исходного треугольника, то три таких прямые пересекутся в одной точке, лежащих на гиперболе Киперта. В частности, на этой гиперболе лежат точки Торричелли и точки Наполеона (точки пересечения чевиан, соединяющие вершины с центрами построенных на противоположных сторонах правильных треугольников).
Гипербола Енжабека — описанная гипербола, проходящая через ортоцентр и точку Лемуана. На ней лежит центр описанной окружности.
Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности. Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха. В частности, через точку Фейербаха проходит окружность, проведённая через основания биссектрис.
