3.5 Проверка статической прочности вала

Проверка статической прочности осуществляется по значениям

максимальных напряжений σ'_max и τ'_max с учетом возможных перегрузок по формуле эквивалентных напряжений s_экв:

s_экв = , (3.18)

где σ'_max = σ_a ·α_П и τ'_max = τ_max· α_П, причем

- коэффициент перегрузки передачи (здесь Р_дв.н. и Р_дв.р. - соответственно номинальная и расчетная мощности приводного двигателя передачи, Т_max и Т_ном -максимальный и номинальный вращающие моменты на валу двигателя);

[_s] – допускаемое напряжение,

(здесь s_Т - предел текучести материала вала, [_S]_T – требуемый коэффициент запаса по пределу текучести, [_S]_T =1,5÷2).

3.6 Расчет валов на жесткость

Как правило, расчету на жесткость подвергаются валы с отношением опорной длины l_on к среднему диаметру d_cp между опорами более 8. Это валы коробок скоростей, несущих блоки шестерен и большое число колес. Обязательно проверяются расчетом на жесткость валы-червяки. Вопросы расчета подробно освещены в пособии [9].

Для валов-червяков ориентировочное значение прогиба f определяется по формуле:

(3.19)

где F_t1 и F_r1 – окружная и радиальная силы на червяке, Н;

Е – модуль упругости, Е=2,1510⁵ МПа для стали;

- приведенный момент инерции поперечного сечения червяка, мм⁴ (здесь и - диаметры впадин и вершин витков червяка, мм);

l – расстояние между опорами вала-червяка, мм;

[f] = (0,005…0,01)·m – допускаемое значение прогиба, мм (здесь m – модуль зацепления, мм).

При расчете каждого вала есть свои особенности, которые уточняются с руководителем проекта. Ниже приведена примерная последовательность расчета вала червячного редуктора с шестерней открытой зубчатой передачи на выходном конце.

4 Пример расчета.

4.1 Вычерчивание исходной схемы.

Используются условные изображения элементов передач, валов и опор на кинематических схемах. Под исходной схемой помещается расчетная схема, в которой все силы и моменты приводятся к точкам на оси вала, а действие опор заменяется опорными реакциями в системе координатных осей X, Y, и Z . Особое внимание следует обращать на направление внешних сил и моментов. Направление опорных реакций при составлении расчетной схемы неизвестно, в связи с чем их рекомендуется вычерчивать штриховыми линиями. Под расчетной схемой помещаются эпюры M_ux,y и M_z Эпюры рекомендуется строить в масштабе с целью получения большей наглядности при оценке сечения вала.

4.2 Исходные данные для расчета.

Принимаются по данным кинематического расчета, расчета передач и эскизного прочерчивания передачи (компоновки).

Диаметры участков вала из расчета на кручение по компоновке:	Силы и диаметры элементов передач:	Длины участков валов (по компоновке):
мм;	Н;	а = 140 мм;
мм;	1275 Н;	в = 140 мм;
мм;	1300 Н;	с = 100 мм.
мм;	475 Н;
	200 Н;
	мм;
	мм;

4.3 Выбор материала вала.

Учитывая повышенные требования к жесткости (наличие червячной передачи) и отсутствие требований к габаритам вала, назначаем относительно дешевую, хорошо обрабатываемую сталь Ст5 (таблица 1.1).

σ_в =500…600 МПа;

σ_T =270 МПа;

σ_-1 =250 МПа;

τ_-1=150 МПа.

Допускаемое напряжение изгиба определяется с учетом цикла нагружения вала по изгибу:

МПа.

4.3 Значение моментов на схеме

,Н·мм

, Н·мм

4.4 Определение значения опорных реакций

(используют уравнения статического равновесия вала).

В качестве примера приведена последовательность определения опорных реакций в плоскости Y0Z (вертикальная плоскость).

4.4.1. Действующие силовые факторы и определяемые реакции:

4.4.2. Нахождение F_RCy:

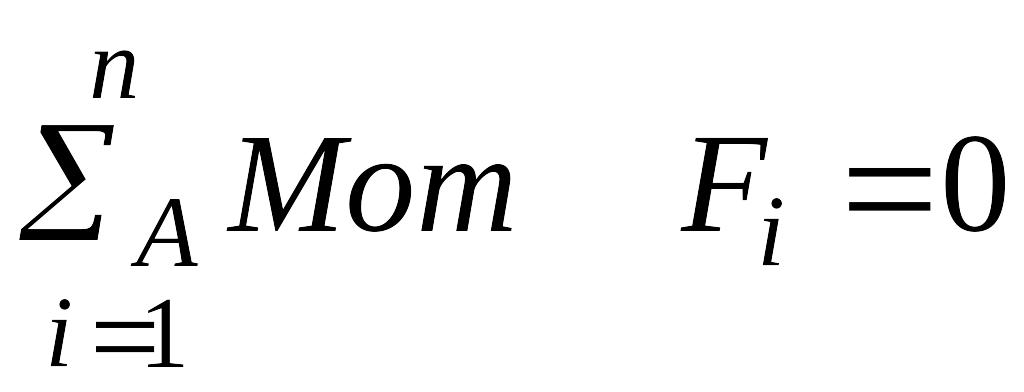(в уравнении моментов задаются положительным направлением против часовой стрелки)

= 1825 Н.

4.4.3. Нахождение F_RAy:

Знак (-) означает, что ранее принятое направление опорной реакции неверно, следует сплошной линией показать истинное направление реакции.

4.4.4. Проверка правильности определения значений реакций F_RAy и F_RCy (через сумму проекций всех сил вертикальной плоскости на ось Y с учетом истинного направления):

Реакции найдены верно.

4.4.5. Значения опорных реакций

По аналогам с п.п. (4.4.1…4.4.5.) находим:

F_Rax = 1900 H

F_Raz = 200 H

F_RCx =4100 H

Истинное направление реакций показано сплошными линиями.

4.4.6. Суммарные опорные реакции

(необходимы для выбора подшипников)

4.5 Определение значений внутренних силовых факторов.

На этом этапе следует вспомнить, что эпюра моментов:

- строится на сжатых волокнах (правило «зонтика»);

- имеет «скачки» в месте приложения сосредоточенных моментов, как

изгибающих, так и крутящих;

- изменяется на участках в зависимости от сил (наклонные прямые для

сосредоточенных сил, криволинейные очертания для распределенной

нагрузки).

Определение значений моментов производим для характерных точек вала А, В, С и Д.

Рекомендуется делать это при подходе к точке «слева» и «справа».

4.5.1. Моменты изгибающие M_ux и M_uy, Н·мм.

Точка	Mux		Muy
	слева	справа	слева	справа
А	0	0	0	0
В	-10500	-50500	266000	266000
С	-127500	-127500	350000	350000
Д	0	0	0	0

Например, для точки “B” «слева» :

M_{ux слева} = – F_Ray·a = – 75·140 = – 10500 Н·мм

Для точки “B” «справа»:

4.5.2. Суммарные изгибающие моменты M_uε

Точка	Момент Н·мм
	слева	справа
А	0	0
В	266207	270751
С	372500	372500
Д	0	0

4.5.3. Крутящий момент M_z на валу.

Точка	Mz, Н·мм
А	0
В	262500
С	262500
Д	262500

M_z= -Т =262500 Н·мм.

4.5.4. Эквивалентный момент М_экв.

Точка	Мэкв, Н·мм
А	0
В	377110
С	455700
Д	262500

4.6 Уточнение значений диаметров di по эквивалентному моменту Мэкв и допускаемому напряжению [σ -1]u

Точка	Расчетное значение диаметра di, мм	Принято ранее из компоновки
А	0	55
В	39,76	55
С	42,35	55
Д	35,24	45

Как видно, отличие диаметров достигает 28% в точке “B”. Точку “A” не следует принимать во внимание, так как здесь диаметр определяется чисто из конструктивных соображений.

Желательно уточнить значение диаметров, после рекомендуемое отличие от расчетных не должны превышать 10…15%.

Окончательно принимаем значения, учитывая, что в точке “A” используется такой же подшипник, как в точке “C”.

Точка	Значение диаметра di, мм
А	45
В	50 (с учетом ослабления вала шпоночным пазом под червячное колесо
С	45
Д	38 (с учетом ослабления вала шпоночным пазом под шестерню открытой передачи)

4.7 Назначение опасного сечения.

Этим сечением является то, для которого коэффициент запаса прочности принимает наименьшее значение по сравнению с остальными значениями.

Предварительно для оценки «опасности» сечения можно использовать отношение с учетом наличия концентратора напяжений (шпоночные пазы в точках “B” и “Д “, натяг в точках “B” и “C” от посадки соответственно червячного колеса и подшипника, галтель от перехода участка ВС на участок СД).

Точка	Отношение , Н
А	0
В	7542
С	10127
Д	6908

Как видно, наиболее опасным можно считать сечение под подшипником в точке “C”. Дальнейшие расчеты ведем для данного сечения.

4.8 Анализ расчетного сечения.

Необходимо вычертить эскиз вала в расчетном сечении с прилегающими участками.

Вал шлифуется (R_a=032 мкм), подвергается улучшению.

Подшипник устанавливается на вал с натягом по посадке L0/к6, которая вызывает концентрацию напряжений, равно как галтель радиуса

r = 1 (принимается по фаске f в отверстии насаживаемой детали,

r =(0,7…0,8)f ). Более точно галтели задаются в справочной литературе.

4.9 Определение коэффициентов в формуле запаса прочности

(использованы рекомендации [8, c.146…147] и таблицы 3.3…3.8)

Коэффициент	Концентратор
	Натяг	Галтель
Kσ	1,91*	1087
Kτ	1,28*	1,57
K d σ	0,83	0,83
K d τ	0,72	0,72
KF	1,0	1,0
(ψσ)	0,1	0,1
(ψτ)	0,05	0,05
KV	1,0	1,0

* Получены интерполяцией табличных данных

4.10 Оценка «опасности» концентратора.

Отношение	Натяг	Галтель
Kσ / K d σ	2,3	2,25
Kτ / K d τ	1,78	2,18

Натяг является более опасным для изгиба, а галтель – для кручения.

4.11. Определение геометрических характеристик опасного сечения (круглое, d = 38 мм).

4.11.1. Момент сопротивления изгибу W_{u нетто} (нет ослабления)

W_{u нетто} = W_u= 0,1d³= 0,1· 38³ = 5487,2 мм³

4.11.2. Момент сопротивления кручению W_{к нетто} (нет ослабления)

W_{к нетто} = W_к= 0,2d³= 0,2· 38³ = 10974,4 мм³

4.12 Напряжения в сечении.

4.12.1. Напряжения изгиба σ_a и σ_m.

МПа;

σ_m=0.

4.12.2. Напряжение кручения τ_a и τ_m.

МПа.

4.13. Коэффициент запаса прочности по изгибным напряжениям

(концентратор - натяг).

где МПа

(здесь )

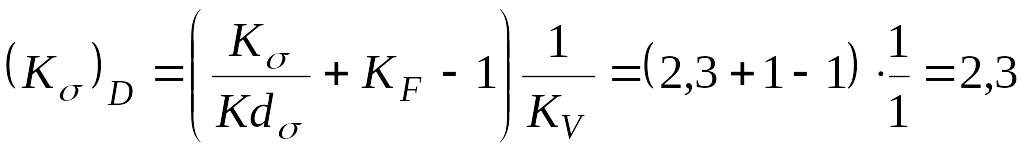4.14. Коэффициент запаса прочности по касательным

напряжениям (концентратор – галтель)

где МПа

(здесь )

4.15. Общий коэффициент запаса прочности S

Полученное значение S =2,03 обеспечивает условие прочности условию сопротивления усталости.

4.16. Оценка статической прочности вала.

Для нашего случая задаемся значением коэффициента перегрузки _П=2,2. В конкретных случаях необходимо производить расчет по формуле 3.21.

σ'_max = σ_a ·α_П = 49,34 ·2,2 = 108,55 МПа;

σ'_max = τ_max ·α_П =2·τ_a ·α_П = 2·11,96 ·2,2 = 52,62 МПа;

МПа

(здесь [S]_T = 1,5 принято)

МПа

σ_экв = 120,63<[σ]=180 МПа

Условие прочности выполнено.

Расчет на жесткость не выполняется в связи с достаточно большим запасом прочности S=2,03 > [S]_T = 1,5.