3 Расчет валов

При расчете валов учитывают изгибающие и крутящие моменты и расчет ведут в два этапа:

- проектировочный расчет и конструирование вала, при котором устанавливают диаметры характерных сечений вала из расчета на прочность и конструируют вал с учетом возможности свободного продвижения деталей вдоль вала до места их посадки и осевой фиксации этих деталей на валу;

- уточненный (проверочный) расчет - служит для определения коэффициента запаса прочности для предположительно опасных сечений вала. Проводится после выполнения сборочного чертежа редуктора.

3.1 Общие рекомендации

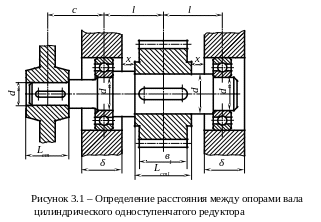
Для определения реакций опор вала и построения в дальнейшем эпюр изгибающих и крутящих моментов необходимо знать расстояние между опорами, а также расстояния между находящимися на валу деталями (зубчатыми колесами, шкивами, звездочками, муфтами и т.д.) и опорами. Для уменьшения прогибов валов рекомендуется располагать насаживаемые детали ближе к опорам. Расстояние между опорами вала зависит от конструкции редуктора и определяется по компоновочному чертежу.

На рисунках 3.1...3.5 показано, какие размеры из компоновочного чертежа редуктора должны быть отражены в расчетной схеме вала.

3.2 Силы, действующие на вал

Основными нагрузками, вызывающими деформацию изгиба валов, являются силы в зубчатых и червячных зацеплениях, натяжения ветвей ремня или цепи соответствующих передач. Силу в зацеплении зубчатых колес или червячной пары раскладывают на три взаимно перпендикулярные составляющие. Окружная сила F_t направлена по касательной к начальным окружностям зубчатых колес; радиальная сила F_r - по радиусу к центру колеса и осевая сила F_a - параллельно оси вала. Потерями на трение пренебрегают и считают, что сила от зуба шестерни на зуб колеса равна и противоположно направлена соответствующей силе от зуба колеса на зуб шестерни (рисунок 3.6). Силы, действующие в зацеплении, определяют по формулам в таблице 3.2.

Таблица 3.2 – Силы, действующие в зацеплении

Вид передачи и силы в зацеплении	Шестерня	Колесо
1. Цилиндрические зубчатые передачи
Окружные
Радиальные
Осевые	Fa1 =Ft1 ·tgβ
2. Конические зубчатые* передачи
Окружные
Радиальные		Fr2 = Fa1
Осевые		Fa2 = Fr1
3. Червячные передачи
Окружные
Радиальные	Fr1 = Fr2 ≈ Ft2 ·tgα
Осевые	Fa1 = Ft2	Fa2 = Ft1

* Направление винтовой линии зубьев совпадает с направлением вращения колеса, причем β_m – угол наклона зуба в среднем сечении (обычно β_m=35^о).

Здесь: Т₁ и Т ₂ – вращающие моменты на ведущем и ведомом валах (во второй ступени передачи индексы 1 и 2 заменяются соответствующими индексами 3 и 4).

Значения моментов принимаются из кинематического расчета либо определяются по формуле:

Т=Р/ω, Н·м, (3.1)

где Р – мощность на валу, Вт;

ω – угловая скорость, рад/с;

d₁ и d₂ – делительные диаметры шестерни и колеса или червяка и червячного колеса, мм (в передачах без смещения делительные и начальные диаметры равны; для конических колес используются значения диаметров колес d₁ и d₂ в средних сечениях колес);

α=20^о – угол зацепления в нормальном сечении зуба или профильный угол в осевом сечении червяка червячной передачи;

β – угол наклона зубьев, град.;

δ₁ и δ₂ – половины углов при вершинах делительных конусов шестерни и колеса конической передачи, связанные с передаточным числом u зависимостью:

u=tgδ₂=ctgδ₁ (3.2)

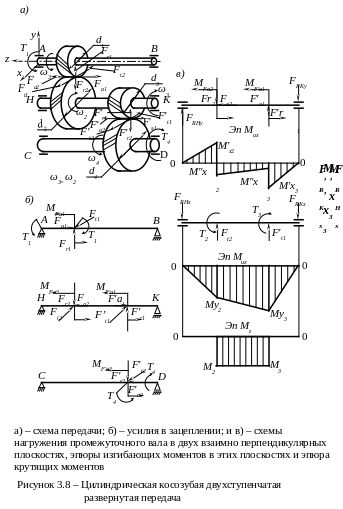
На рисунках 3.6…3.14 приведены исходные схемы и возможные эпюры изгибающих и крутящих моментов для валов различных передач. Особо отметим, что характер эпюры определяется конкретным отношением значений сил, положением элементов передач на валу и опор вала. Следует помнить, что осевые силы передач создают сосредоточенные изгибающие моменты и определяют «скачки» на эпюрах. Общие правила построения эпюр рассматриваются в курсе сопротивления материалов. При этом эпюры строятся на сжатых волокнах сечения вала.

Для уменьшения результирующей осевой силы на промежуточных валах цилиндрических передач с косозубыми колесами следует выбирать направление зубьев колеса первой ступени и шестерни второй ступени одинаковым, при этом осевые силы на промежуточном валу F_a2 и F^'_a1 направлены в разные стороны (рисунок 3.7 и 3.8).

В конической прямозубой передаче радиальная сила на шестерне равна осевой силе на колесе F_r1 =F_a2 , а осевая сила на шестерне равна радиальной силе на колесе F_a1=F_r2, причем осевые силы всегда направлены от вершин к основаниям конусов. На рисунках 3.9 и 3.10 плоскость X-Z является горизонтальной плоскостью для шестерни и для колеса, плоскость Y-Z - вертикальной плоскостью для шестерни и плоскость X-Y - вертикальной плоскостью для колеса, F_к - внешняя сила.

В червячной передаче потерями на трение из-за их значительной величины пренебрегать нельзя. Поэтому Т₂ = T₁·u·h, где h ≈ 0,7¸0,85 – КПД передачи (уточняется в расчете).

На рисунках 3.11…3.14 плоскость X-Z является горизонтальной плоскостью для червяка и для колеса, плоскость Y-Z - вертикальной плоскостью для червяка и плоскость X-Y - вертикальная плоскость для колеса. На рисунке 3.13 показан промежуточный вал и нагрузка, действующая на него: эпюра изгибающих моментов в вертикальной плоскости построена по правилам ортогонального проектирования, а эпюра изгибающих моментов в горизонтальной плоскости - с использованием аксонометрии. Для разгрузки промежуточного вала двухступенчатой червячной передачи от осевых воздействий направление нарезки червяка второй ступени и направление зубьев колеса первой ступени должны совпадать (рисунок 3.14).

Если на входе или на выходе редуктора имеется открытая зубчатая или червячная, цепная или ременная передача, то на соответствующий вал редуктора действуют на консоли изгибающие силы F_к от этих передач (рисунок 3.9 и 3.10).

При наличии открытой зубчатой или конической передачи нагрузки на вал определяются аналогично нагрузкам от сил, действующих соответственно в закрытой зубчатой или конической передаче.

Нагрузка на вал от натяжения цепной передачи несколько больше окружной силы F_t, из-за дополнительного натяжения цепи её собственным весом.

F_a = K_в ·F_t , (3.3)

где К_в – коэффициент, учитывающий влияние провисания ветви цепи.

Для горизонтальной передачи и при угле наклона передачи менее 40^о коэффициент К_в=1,15, при угле наклона передачи более 40^о и для вертикальной передачи К_в=1,05. Приближенно можно считать, что сила F_a направлена по линии центров звездочек.

Давление на валы в ременных передачах определяют исходя из следующего: сумма натяжений обеих ветвей ремня в ненагруженной и работающей передаче не изменяется 2F₀ = F₁ + F₂, провисание ремня существенно не нагружает валы, натяжения от центробежных сил взаимно уравновешиваются в ремне и даже способствуют нагрузке валов. Поэтому давление на валы:

F_a = 2F₀ ·Z·sin , (3.4)

где F_о – предварительное натяжение каждой ветви ремня, Н;

Z – число ремней;

d – угол обхвата малого шкива.

Для плоскоременных передач:

F_a = К_мн·2F₀ ·sin , (3.5)

где К_мн=1,5 – коэффициент, учитывающий максимальное начальное натяжение ремня с учетом последующего ослабления.

При выполнении курсовых проектов можно считать, что сила F_a в ременных передачах направлена по линии центров шкивов. При наличии соединительной муфты на вал действует неуравновешенная сила, определяемая конструкцией муфты (8, с.274…306). В общем случае консольная сила F_к от муфты прикладывается по середине ступицы полумуфты, причем ее значение можно найти по формуле (3.6):

, (3.6)

где К – коэффициент, значение которого определяется типом муфты, (обычно К=0,15...0,4)

Т – момент на валу, Н ∙ мм;

D_сэ – диаметр расположения силовых элементов, мм (расположение пальцев в муфтах типа МУВП, делительный диаметр звездочек в цепных муфтах, делительный диаметр зубчатой полумуфты и т.д.).