
Корреляция и регрессия
Между двумя случайными величинами может существовать статистическая связь, состоящая в том, что значение, принятое одной величиной – Х, сказывается на значении другой величины – Y.
Например, существует статистическая зависимость между ростом человека Н и его весом Р.
Количественно величину статистической связи между случайными величинами выражают с помощью коэффициента корреляции (r), который определяется следующей формулой:
![]() ,
,
где X и Y – среднеквадратические отклонения; М – знак математического ожидания.
Свойства коэффициента корреляции:
1. Величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин Х и У.
2. Величина коэффициента корреляции заключена в пределах –1 r 1.
3. Если r 0, то с увеличением Х соответствующие им значения Y в среднем уменьшаются, т.е. существует обратная связь.
4. Если r 0, то с увеличением Х соответствующие им значения Y в среднем растут, т.е. существует прямая связь.
5. Если r = 0, то между параметрами нет линейной корреляционной связи, (но может существовать нелинейная корреляционная зависимость).
6. Значение r = 1 появляется обычно тогда, когда между величинами X и Y существует линейная функциональная связь (крайне редкая в медико-биологических исследованиях).
Выборочный коэффициент корреляции
При обработке результатов выборочного обследования находят выборочный коэффициент корреляции по формуле:
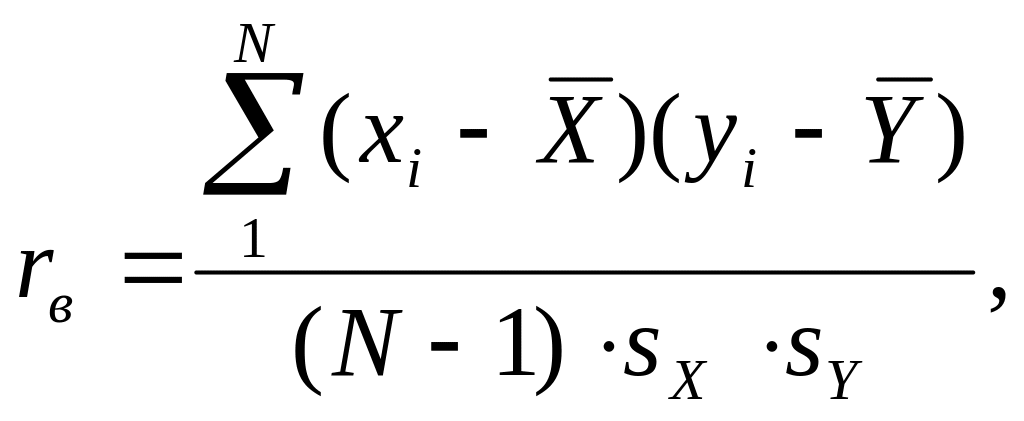
где
![]() – выборочные средние; sX
и sY
– выборочные СКО.
– выборочные средние; sX
и sY
– выборочные СКО.
Если N , то выборочный коэффициент стремится к истинному значению коэффициента корреляции.
Выборочный коэффициент корреляции используют для аналитической записи статистической связи между случайными величинами с помощью уравнения регрессии:
![]() .
.
После раскрытия скобок уравнение записывается в стандартном виде y = kx + g.
![]()
Это уравнение позволяет находить наиболее вероятное значение случайной величины Y в соответствии со значением, принятым случайной величиной Х.
Рассмотрим следующий пример.
Два способа оценки митральной регургитации
Используя данные, представленные в таблице, вычислим коэффициент корреляции между значениями фракции регургитации, полученными двумя этими методами, и найдем коэффициенты линейной регрессии k и g .
|
N = 21 |
|
|
|
Доплер - x |
Катетеризация - y |
|
|
0,49 |
0,62 |
0,00 |
|
0,83 |
0,72 |
0,08 |
|
0,71 |
0,63 |
0,03 |
|
0,38 |
0,61 |
-0,01 |
|
0,57 |
0,49 |
0,00 |
|
0,68 |
0,79 |
0,06 |
|
0,69 |
0,72 |
0,05 |
|
0,07 |
0,11 |
0,16 |
|
0,75 |
0,66 |
0,04 |
|
0,52 |
0,74 |
0,01 |
|
0,78 |
0,83 |
0,10 |
|
0,71 |
0,66 |
0,04 |
|
0,16 |
0,34 |
0,05 |
|
0,33 |
0,50 |
0,00 |
|
0,57 |
0,62 |
0,01 |
|
0,11 |
0,00 |
0,18 |
|
0,43 |
0,45 |
0,00 |
|
0,11 |
0,06 |
0,16 |
|
0,31 |
0,46 |
0,01 |
|
0,20 |
0,03 |
0,13 |
|
0,47 |
0,50 |
0,00 |
|
|
|
|
|
0,47 |
0,50 |
r |
|
0,243 |
0,255 |
0,888 |
|
|
|
|
|
|
|
Коэффициенты |
|
|
|
|
Построение линии регрессии: y = kx + g |
|
k |
g |
|
|
|
|||||
|
|
|
|
|
|
|
0,934 |
0,063 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Расчет регрессии - предсказание результатов катетеризации по результатам доплер-исследования
Таблица упорядочена по величине доплеровских значений фракции регургитации. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
N = 21 |
Результат регрессии |
|
|||||||||||||
Доплер - x |
Катетеризация - y |
|
|||||||||||||
0,07 |
0,11 |
0,13 |
|
||||||||||||
0,11 |
0,00 |
0,17 |
|
||||||||||||
0,11 |
0,06 |
0,17 |
|
||||||||||||
0,16 |
0,34 |
0,21 |
|
||||||||||||
0,20 |
0,03 |
0,25 |
|
||||||||||||
0,31 |
0,46 |
0,35 |
|
||||||||||||
0,33 |
0,50 |
0,37 |
|
||||||||||||
0,38 |
0,61 |
0,42 |
|
||||||||||||
0,43 |
0,45 |
0,46 |
|
||||||||||||
0,47 |
0,50 |
0,50 |
|
||||||||||||
0,49 |
0,62 |
0,52 |
|
||||||||||||
0,52 |
0,74 |
0,55 |
|
||||||||||||
0,57 |
0,49 |
0,60 |
|
||||||||||||
0,57 |
0,62 |
0,60 |
|
||||||||||||
0,68 |
0,79 |
0,70 |
|
||||||||||||
0,69 |
0,72 |
0,71 |
|
||||||||||||
0,71 |
0,63 |
0,73 |
|
||||||||||||
0,71 |
0,66 |
0,73 |
|
||||||||||||
0,75 |
0,66 |
0,76 |
|
||||||||||||
0,78 |
0,83 |
0,79 |
|
||||||||||||
0,83 |
0,72 |
0,84 |
|
||||||||||||

