Приложение 2 формулы расчета mx измерительных каналов иис

1. Расчет ƒ_н(x).

Исходные данные из п. 3.1 подставляем в следующие формулы:

 при i =1,2,...., N-1;

A^N= 1;

.

Затем вычисляем

ƒ_н(x)=A^°x + a.

2. Расчет М[Δ_с(х)], σ[Δ_с(х)].

На основании исходных данных из п. 3.1.2 вычисляем вспомогательные величины:

Вⁱ= (В_к+А_к) при i=0,1,...,N-1;

Q = [(В_к+А_к)²+G при i=0,1,...,N-1;

B^N=A^N= =1;

Aⁱ= А_к при i=0,1,...,N-1;

b= - ;

B=B˚- A˚.

Подставляем их в следующие формулы:

М[Δ_с(х)]=Bx+b

σ[Δ_с(х)]=<x²[Q -(B˚)²]+ >^1/2.

3. Расчет Δ_с.д.

Используем исходные данные п. 3.1.3 для вычисления вспомогательных величин; обозначим λ_i = Δ_с.дi, q₁ = q, тогда:

q_i = q_i-1A_i-1 при i=2,3,...,N;

B^N=1; B^i-1=Bⁱ(A_i+2λ_i/q_i) при i=2,3,...,N-1.

Затем вычисляем

.

4. Для вычисления М(Δ_сi) и σ(Δ_сi) используем исходные данные п. 3.1.4.

Обозначим:

y_oi = x_i - входной сигнал i-го канала компонента.

Вычислим вспомогательные величины:

 при s = 1,2,...,N;

 при s=2,3,...,.N,

где A_iis =A_is; A_кis = 0 при k ≠ i

y_si имеет смысл математического ожидания выходного сигнала i-гo канала s-гo блока.

Дальнейшие вычисления проводят по формулам:

σ(Δ_с.i) = σ_Ni(Δ_с).

5. Расчет σ_д( ).

Для вычисления σ_д( ) ИК используем исходные данные п. 3.1.4.

Обозначим

q₁ = q;

λ_i = Δ_с.дi;

 при i =1,2,…,N.

Вычислим вспомогательные величины:

q_i = q_i-1 A_i-1 при i = 2,3, ...,N;

B^N = S_N = 1;

В^i-1 = Вⁱ(А_i + ) при i= 1 ,2, . .N;

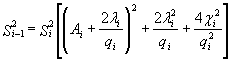 при i= 1 ,2, . .N;

C_i,i+1=1;

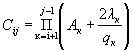 при j > i+1.

Затем вычислим

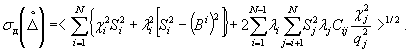
6. Расчет Δ_д.

Для вычисления Δ_д используем исходные данные п. 3.1.6.

Введем обозначения:

_i = α_iδ_i;

 при i= 1 ,2, . .N.

Здесь  - параметр перебора, который при каждом i= 1 ,2, . .N принимает значения 0 или 1.

Вычислим по формулам приложения 3, п. 3 вспомогательные величины Bi, Вi, , С_ij, q_i.

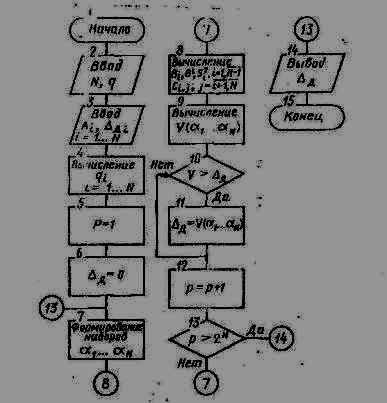
Введем функцию V (α₁, α₂, …, α_N) от величины α_i:

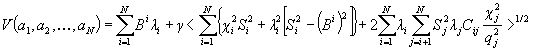
Расчет Δ_д соответствует задаче поиска max V(α₁, …, α_N) при условии, что α_i может принимать одно из двух значений α_i =0 или α_i =1.

Например, при N = 3 необходимо вычислить восемь значений V(0, 0, 0), V (0, 0, 1), V (0, 1, 0), V (1, 0, 0), V (1, 0, 1), V (0, 1, 1), V (1, 1, 0), V (1, 1, 1) и выбрать наибольшее из них.

7. Расчет ψ_M(Δc) (ξ₁, ξ₂, …, ξ_p); ψ_σ(Δc) (ξ₁, ξ₂, …, ξ_p).

Для вычисления функций влияния используем исходные данные п. 3.2.1.

Вычислим вспомогательные величины:

B_iξ=B_i+α_2i(ξ₁, …, ξ_p); b_iξ=b_i+α_1i(ξ₁, …, ξ_p); ; .

Подставив их в формулы приложения 2, п. 2, вычислим  при i = l, 2, .... N.

Эти величины используем для вычисления М[Δ_с(х)] и подставим их в формулы приложения 3, п. 2 вместо R, , b.

Затем по формулам приложения 2, п. 2 вычислим  и .

Затем вычислим искомые функции влияния:

ψ_M(Δc) (ξ₁, ξ₂, …, ξ_p) =  - ;

ψ_σ(Δc) (ξ₁, …, ξ_p) =  - .

8. Расчет ΔΔ_с.д.

Для расчета используют исходные данные п. 3.2.2. Вычислим вспомогательные величины λ_iξ  при i = 1, 2, ..., N:

λ_iξ = (1+K_i) λ_i.

По формулам приложения 2, п. 3 вычислим Δ_с.д. Используя λ_iξ вместо λ_i по формулам приложения 2, п. 3 вычислим Δ_с.д(ξ₁, …, ξ_p). Требуемую характеристику находят по формуле

ΔΔ_с.д(ξ₁, …, ξ_p) = KΔ_с.д,

где K= (Δ_с.д(ξ₁, …, ξ_p))/ Δ_с.д.

9. Расчет Δ_д( )(ξ₁, …, ξ_p).

Для расчета используют исходные данные п. 3.2.3.

Вычислим вспомогательные величины λ_iξ, χ_iξ:

λ_iξ = (1+K_i) λ_i;

χ_iξ = (1+l_i) χ_i.

По формулам п. 3.1.5 вычислим σ_д( ). Используя λ_iξ, χ_iξ вместо λ_i и χ_i, по формулам приложения 3 п.5, вычислим σ_дξ( ).

Искомую характеристику находят по формуле

Δσ_д( )(ξ₁, …, ξ_p)=l σ_д( ),

где l=[ σ_дξ( )-σ_д( )]/σ_д( ).

10. Расчет ΔΔ_д(ξ₁, …, ξ_p).

Для расчета используют исходные данные п. 3.2.4.

Вычислим вспомогательные величины δ_iξ

δ_iξ =(1+r_i) δ_i.

По формулам приложения 2 п. 6 вычислим Δ_д. Используя δ_iξ вместо δ_i, вычислим Δ_дξ по формулам приложения 2 п. 6.

Искомую характеристику находим по формуле

ΔΔ_д = rΔ_д,

где r=(Δ_дξ - Δ_д)/ Δ_д.

11. Расчет MX ИК в стационарном динамическом режиме в нормальных условиях.

Для расчета используют исходные данные п. 4.1. Номинальную АЧХ ИК и наибольшее допустимое отклонение от нее рассчитывают по формулам

Номинальную ФЧХ ИК и наибольшее допустимое отклонение от нее рассчитывают по формулам

;

.

Спектральную плотность случайной составляющей ИК рассчитывают по формуле

.

12. Расчет MX ИК в стационарном динамическом режиме в рабочих условиях эксплуатации.

Для расчета используют исходные данные пп. 4.1 и 4.2.

Рассчитывают вспомогательные величины ΔA_ξ (ω), Δφ_ξ(ω), S :

;

;

.

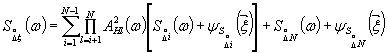Используя данные приложения 2, п. 11, находят функции влияния , , :

=ΔA_ξ(ω) - ΔA(ω);

=Δφ_ξ(ω) - Δφ(ω);

=S (ω) - S (ω).

Примечание к п.7. Для наиболее сложного алгоритма расчета Δ_д приведена блок-схема. Программа составляется в зависимости от типа используемой ЭВМ.