7.Индекс выгодности инвестиций.

(показатель Profitability Index)

Аббревиатура: PI.

PI- это отношение отдачи капитала к вложенному капиталу.

Для реальных инвестиций (инвестиций в материальный (вещественный) капитал ), длящихся несколько лет, показатель PI подсчитывается по формуле :

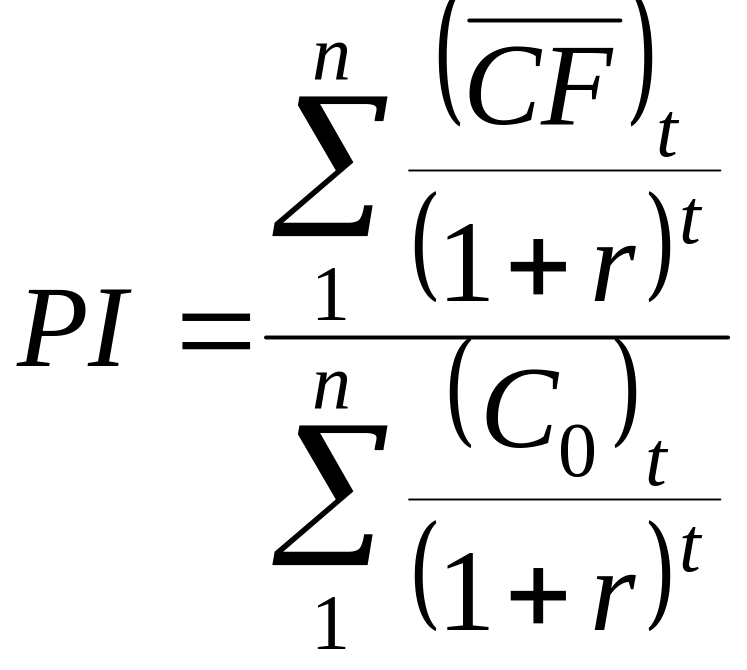, (24)

Где - финансовый итог в году t, подсчитанный без первоначальный инвестиций (если они приходятся на этот год);

-отдача капитала (первоначальных инвестиций) сумма финансовых итогов по годам, считая с даты первых инвестиций;

первоначальные инвестиции (original capital) в году t, считая от даты начала инвестиций;

вложенный капитал (первоначальные инвестиции).

Для финансовых инвестиций формула подсчёта PI имеет более простой вид:

, (25)

где финансовый итог в году t, считая от даты покупки финансовых активов;

- cумма финансовых итогов по годам (отдача на вложенный капитал);

-разовые инвестиции в финансовые активы (вложенный капитал).

Правило PI : принимаются инвестиционные проекты , в которых значение PI превышает единицу.

Иные названия PI:

Индекс прибыльности;

Benefit-cost ratio - соотношение приведённых доходов к приведённым на эту же дату инвестиционным расходам (условно рентабельность).

Термин “Profitability“ может быть переведён на русский язык как прибыльность, доходность, рентабельность, выгодность. Поскольку в расчётных формулах PI не фигурирует ни прибыль , ни доход, наиболее приемлемым названием для PI является индекс выгодности.

Выражение “Benefit-cost ratio” Может быть переведено как отношение суммарной выгоды к расходам (затратам), что по смыслу равноценно отношению отдачи капитала к вложенному капиталу.

8.Период окупаемости инвестиций.

(показатель Payback period)

Payback period - это период, за который отдача на капитал достигает значения суммы первоначальных инвестиций.

Под отдачей на капитал в случае реальных инвестиций (инвестиций в материальные (вещественные) активы ) понимается сумма дисконтированных финансовых итогов по годам, подсчитанных без первоначальных инвестиций:

, (26)

Где – финансовый итог в году t, подсчитанный без первоначальных инвестиций (если они приходятся а этот год) .

В случае финансовых инвестиций отдачу капитала подсчитывают по аналогичному выражению:

, (27)

где - финансовый итог в году t, считая от даты покупки финансовых активов.

К первоначальным реальным инвестициям относят затраты на капитальное строительство и эксплуатационные расходы, финансируемые за счёт уставного фонда и заёмных средств.

К первоначальным финансовым инвестициям относят затраты на покупку акций , векселей облигаций и иных ценных бумаг.

Показатель Payback period наиболее близок по своему содержанию к традиционному показателю “Срок окупаемости” (капитальных вложений). Разница между ними состоит в том , что при подсчёте Payback period учитывают все первоначальные инвестиции (капитальные расходы и эксплуатационные расходы), а при подсчёте “Срока окупаемости” учитывают только первоначальные капиталовложения.

В литературе можно встретить утверждение о том, что Payback period является альтернативным показателем для Net present value.

Однако эти показатели характеризуют инвестиционный проект с разных сторон и измеряются в разных единицах.

Опубликованные переводы термина “Payback period”:

Период окупаемости (капиталовложений);

Период окупаемости;

Период окупаемости инвестиций (20);

Срок окупаемости.

В первом переводе говорится лишь о капиталовложениях, составляющих часть инвестиций. Во втором и четвёртом вовсе не указаны инвестиции. Третий перевод представляется наиболее удачным.

Опубликованные трактовки термина “Payback period”:

Число лет, которое проходит, пока суммарный поток наличности от проекта не сравняется с первоначальной суммой инвестиций;

Отношение первоначального вклада к ежегодным наличным поступлениям (20);

Продолжительность периода , в течени которого сумма чистых доходов дисконтированных на момент завершения инвестиций, равна сумме инвестиций. Теоретически необходимое время для полной компенсации инвестиций дисконтированными доходами.

Вторая трактовка определяет термин “Payback period” в виде безразмерного индекса , что не соответствует названию термина. В третьей трактовке финансовые итоги (Cash flow) необоснованно заменены на доходы.

9.Обоснование эффективности инвестиционных проектов.

При принятии решений в бизнесе о долгосрочных инвестициях возникает потребность прогнозировать эффективность капитальных вложений. Для этого нужен долгосрочный анализ доходов и издержек.

Основными методами оценки программы капитальных вложений является методы окупаемости инвестиций (РР); расчёта отдачи на вложенный капитал (PI); дисконтирования денежных поступлений (IRR); чистой текущей стоимости (NPV).

9.1. Первый метод оценки капитальных вложений заключается в определения срока, необходимого для того, чтобы инвестиции окупали себя.

Пример:

	Машина X	Машина Y
Стоимость, млн. грн.	100	100
Прибыль, млн. грн. 1-й год	50	25
2-й год	50	25
3-й год	10	25
4-й год	5	25
5-й год	5	25
6-й год		25
	120	150

Машины X и Y стоят по 100 млн. грн. каждая. Машина X обеспечивает прибыль 50 млн. грн. в год, а машина Y  25 млн.грн. из этого следует, что машина X окупится за два года , а машина Y за четыре года . исходя из окупаемости , машина X , более выгодна , чем машина Y.

9.2. Несмотря на свою простоту метод окупаемости имеет свои недостатки: он не учитывает сроки службы машины и то, что машина Y обеспечивает значительно большую сумму прибыли за весь период эксплуатации. Следовательно, оценивается эффективность капитальных вложений, надо учитывать не только сроки окупаемости инвестиций, но и доход на вложенный капитал (PI) или доходность (рентабельность) проекта:

Из нашего примера видно, что необходимо приобрести машину Y, так как для машины X PI=120/100100%=120%,а для машины Y PI=150/100100%=150%.

Однако это метод имеет свои недостатки: он не учитывает распределения притока и оттока по годам. В рассматриваемом примере денежные поступления на четвертом году имеют такое же значение, как и на первом. Обычно же руководство предприятия более высоким денежным доходам в первые годы. Поэтому оно может выбрать машину Х, несмотря на ее низкую норму прибыли.

9.3. Более научно обоснованной является оценка эффективности капитальных вложений методом дисконтирования денежных поступлений, который учитывает изменение стоимости денег во времени.

Дисконтирование денежных поступлений представляет собой метод оценки программы капитальных вложений, который базируется на дисконтной арифметике и позволяет определить, будут ли давать эти программы необходимый доход. Чтобы понять данную процедуру, сначала рассмотрим сложные процедуры.

Например, если бы нам нужно было вложить в банк 1000тыс. грн., который выплачивает 20% годовых, то мы рассчитали бы показатели доходности:

За 1-й год: 1000(1+20%)=1200 тыс. грн.;

За 2-й год: 1200(1+20%)=1440 тыс. грн.;

З а 3-й год: 1440(1+20%)=1728 тыс. грн.;

Данный пример показывает методику определения стоимости инвестиций при использовании сложных процентов. Сумма годовых процентов каждый год возрастает, мы имеем доход как с первоначального капитала, так и с процентов, полученных за предыдущие годы.

Для определения стоимости, которую будут иметь инвестиции через несколько лет, при использовании сложных процентов применяют формулу (6).

Дисконтирование  расчет сложных процентов наоборот, который производится по формуле (11).

Для того, чтобы через пять лет стоимость инвестиций составляла 500 млн. грн. при ставке 20%, необходимо вложить следующую сумму:

Например, компания рассматривает вопрос о том, стоит ли вкладывать 150,0 млн. грн. в проект, который через два года принесет доход 200 млн. грн. Принято решение вложить деньги только при условии, что годовой доход от этой инвестиции составит менее 10%, который можно получить, если положить деньги в банк. Чтобы через два года получить 200 млн. грн., компания сейчас должна вложить под 10% годовых 165 млн. грн. (2001/1,1^2). Проект дает доход 200 млн. грн. при меньшей стоимости инвестиции (150 млн. грн.), это значит, что ставка дохода превышает 10%, следовательно, проект является выгодным.

Текущая стоимость будущей прибыли при ставке 10%  165 млн. грн. Стоимость инвестиций  150 млн. грн. Проект даст тот же доход, но расходы на него ниже на 15 млн. грн.

9.4. IRR положено в основу метода чистой текущей стоимости, с помощью которого оценивается эффективность капитальных вложений.

Метод чистой текущей стоимости (NPV) состоит в следующем

1.Определяется текущая стоимость затрат (3), т.е. решатся вопрос, сколько инвестиций нужно зарезервировать для проекта.

2. Рассчитывается текущая стоимость будущих денежных поступлений от проекта, для чего доходы за каждый год приводится к текущей дате. Результаты расчетов показывают, сколько средств нужно было бы вложить сейчас для получения запланированных доходов, если бы ставка доходов была равна ставке процентов в банке или дивидендной отдаче капитала. Подытожив текущую стоимость доходов за все годы, получим общую текущую стоимость дохода от проекта (д).

3. Текущая стоимость затрат (з) сравнивается с текущей стоимостью доходов (д). Разность между ними составляет чистую текущую стоимость доходов (NPV)

NPV = Д  З

Если NPV больше нуля, то это значит, что проект принимает больший доход, чем стоимость капитала. Если NPV меньше нуля, то при ставке дохода, равной банковскому проценту, пришлось бы вложить больше средств, в данный проект, для получения будущих доходов, чем в другие проекты, которые дают такие же доходы. Следовательно, проект имеет доходность более низкую, чем стоимость капитала, и поэтому он невыгодный.

А. Предположим, что фирма рассматривает вопрос о том, стоит ли ей вкладывать 360 млн. грн. в проект, который может дать прибыль в первый год 200 млн. грн., во второй  160 и в третий  120. Проценты на капитал составляют 10%. Стоит ли вкладывать средства в этот проект? Чтобы ответить на поставленный вопрос, рассчитаем NPV с помощью дисконтирования денежных поступлений.

Сначала определим текущую стоимость 1 грн. при r=10%.

Год	1-й	2-й	3-й
	0,909	0,826	0,751

Затем рассчитаем текущую стоимость доходов.

Год	Денежные поступления, млн.грн.	Коэффициент дисконтирования	Текущая стоимость доходов,млн.грн
0	(360)	1,0	(360)
1-й	200	0,909	181,8
2-й	160	0,826	132,16
3-й	120	0,571	90,12
			404,8

NPV = 404,08 – 360 = 44,08 млн. грн.

В нашем примере NPV больше нуля. Следовательно, доходность проекта выше 10%. Для получения запланированной прибыли нужно было бы вложить в банк 404 млн. грн. Поскольку проект обеспечивает такую доходность при затратах 360 млн. грн., то он выгодный, так как позволяет получить доходность большую, чем 10%.

Б. Второй проект предусматривает капитальные вложения в сумме 500 млн.грн. Ожидаемая годовая прибыль  120 млн. грн. на протяжении шести лет. Стоимость капитала равна 15%.Выгоден ли этот проект? Обеспечит ли он необходимую отдачу капиталу?

Текущая стоимость 1 грн. при r = 15%.

Год	1-й	2-й	3-й	4-й	5-й	6-й
Коэффициент дисконтирования	0,870	0,756	0,658	0,572	0,498	0,432

Рассчитаем текущую стоимость всего проекта.

Год	Денежные поступления, млн. грн.	Коэффициент дисконтирования	Текущая стоимость, млн. грн.
0	(500)	1,0	(500)
1-й	120	0,870	104,40
2-й	120	0,756	90,72
3-й	120	0,658	78,96
4-й	120	0,572	68,64
5-й	120	0,498	59,76
6-й	120	0,432	51,84

Чистая текущая стоимость денежных поступлений составляет: 454,2 – 500 = -45,8 млн. грн. Она меньше нуля, поэтому проект невыгодный.

Если доходы от инвестиций поступают равномерно на протяжении всех лет, можно использовать сокращенную методику расчета. Вместо того, чтобы умножать денежные поступления за каждый год на соответствующий ему коэффициент дисконтирования, можно умножить годовой доход на сумму этих коэффициентов. В нашем примере мы могли умножить 120 млн. грн. на сумму коэффициентов (0,870 + 0,658 + 0,572 + 0,498 + 0,432 = 3,785) и получить тот же результат  454,2 млн. грн.

В. Третий проект предусматривает капитальные вложения в сумме 400 млн. грн. Годовая прибыль ожидается 100 млн. грн. Процент на капитал в банке равен 10%. Выгоден ли этот проект, если его продолжительность:

А) 5 лет;

Б) 8 лет.

Текущая стоимость 1 грн. при r =10%.

Год	1-й	2-й	3-й	4-й	5-й	6-й	7-й	8-й
Коэффициент дисконтирования	0,909	0,826	0,751	0,683	0,621	0,565	0,513	0,467
Нарастающая сумма коэффициентов	0,909	1,735	2,486	3,169	3,790	4,355	4.868	5,335

Определим чистую текущую стоимость доходов при разной продолжительности проекта.

Год	Денежные поступления доходов за год, млн. грн.	Коэффициент дисконтирования при z=0,10	Текущая стоимость, млн. грн.	Чистая текущая стоимость, млн. грн.
0	(400)	1,0	(400)	
1-5-й	100	3,790	379,0	-21,0
1-6-й	100	4,355	435,5	+35,5
1-7-й	100	4,868	486,8	+86.8
1-8-й	100	5,335	533,5	+133,5

Результаты расчетов показывают, что проект невыгоден при продолжительности пяти лет. Начиная с шестого года, он обеспечивает более высокий доход, чем капитал, который помещен в банке.

9.5. Важной проблемой при прогнозировании эффективности капитальных вложений является рост цен в связи с инфляцией. Для того, чтобы понять методику учета инфляции, необходимо выяснить разницу между реальной и денежной ставкой дохода.

Предположим, инвестор имеет 1 млн. грн., который он желает вложить так, чтобы ежегодно его состояние увеличивалось на 20%. Иначе говоря, вкладывая 1 млн. грн., он надеется через год получить 1,2 млн. грн., тогда покупательная способность его денег будет на 20% выше, чем сейчас, ибо через год он сможет купить на свои деньги на 20% товара больше чем в данный момент. Допустим, что темп инфляции 50% в год. Если инвестор желает получить реальный доход 20% на свой капитал, то он обязан защитить свои деньги от инфляции. Для этого доход в денежном выражении через год должен быть выше первоначального. Инвестору понадобится дополнительно получить 50% денег от вложенного капитала для защиты реальной стоимости своего первоначального вклада и 50% для защиты реального дохода в сумме 0,2 млн. грн. Фактический доход, который должен получить инвестор через год в денежном измерении, должен составить 1,8 млн. грн. (1,0 млн. грн.1,5 + 0,2 млн. грн.1,5).

Таким образом, денежная ставка дохода, которая нужна инвестору для получения реального дохода в 20% и защиты от инфляции в 50%, составит 800 тыс. грн. на 1 млн. грн. инвестиций, т.е. 80%.

Зависимость между реальной и денежной ставкой дохода можно выразить следующим образом:

(1 + r) (1 + i) = 1 + d, d = (1 + r) (1 + i)  1, где r  необходимая реальная ставка дохода (до поправки на информацию); i  темп инфляции, который обычно измеряется индексом различных цен; d  необходимая денежная ставка дохода.

В нашем примере денежная ставка дохода определяется так:

1 + d = 1,2  1,5 = 1,8; d = 1,8 – 1 = 0,8, или 80%.

Если затраты и цены растут одинаковыми темпами, то в методах дисконтирования денежных поступлений можно не учитывать инфляцию. Ситуация изменяется, если затраты и цены растут разными темпами. Здесь нельзя проводить дисконтирование денежных поступлений, выраженных в постоянных ценах по реальной ставке дохода.

Например, компания решает, следует ли ей вкладывать средства в станок, стоимость которого 3,5 млн. грн. Он позволяет увеличить объем продаж на 6 млн. грн. (в постоянных ценах) на протяжении двух лет. Затраты составят 3 млн. грн. Реальная ставка дохода  10%, индекс инфляции  50% в год. В случае реализации проекта цены на продукцию будут расти всего на 30%, а затраты  на 60% в год.

Определим сначала денежную ставку дохода: (1,10  1,5) – 1 = 0,65,или 65%, а выручку, затраты и доход.

1-й год	Реализация Затраты Доход	6 млн. грн.1,3=7,8 млн. грн. 3 млн. грн.1,6=10,14 млн. грн. 7,8-4,8=3,0 млн. грн.
2-й год	Реализация Затраты Доход	6 млн. грн.1,31,3=10,14 млн. грн. 3 млн. грн.1,61,6=7,68 млн. грн. 10,14-7,68=2,46 млн. грн.

Рассчитаем текущую стоимость доходов.

Год	Денежные поступления доходов, млн. грн.	Коэффициент дисконтирования при z=0,65	Текущая стоимость, млн. грн.
0	(3,5)	1,0	(3,5)
1-й	3,0	0,606	1,82
2-й	2,46	0,367	0,90
			2,72

Чистая текущая стоимость составляет 2,72 – 3,5 = -0,78 млн. грн. Результат отрицательный, следовательно, проект невыгодный для компании.

Если бы мы в этом случае применили реальную ставку дохода 10% к денежным поступлениям в текущих ценах, то допустили бы ошибку.

Год	Денежные поступления доходов, млн. грн.	Коэффициент дисконтирования при z=0,10	Текущая стоимость, млн. грн.
0	(3,5)	1,0	(3,5)
1-й	3,0	0,909	2,7
2-й	3,0	0,826	2,5
			5,2

Чистая текущая стоимость доходов в этом случае будет больше нуля и составит 5,2 – 3,5 = +1,7 млн. грн. Это не правильный результат.

Таким образом, учитывая стоимость капитала и уровень инфляции и используя метод дисконтирования денежных поступлений, можно довольно реально оценить доходность инвестиционных проектов в перспективе.

Приложение