Подання дійсних чисел у двійковому нормалізованому виді

Одержавши двійкове подання, потрібно його нормалізувати, тобто двійкове число повинно завжди починатися з одиниці й мати такий вигляд:

± 1.m₂* 2 ^p

де m₂ — двійкова мантиса числа.

^р — порядок двійкового числа.

^{ПРИКЛАД 3.}

±1.0d → ± 1.0b* 2⁰

Машинні формати дійсних чисел

Як ми вже з'ясували, дійсні базові величини можуть бути типу float (single), double або long double (extended). Всі вони мають для зберігання комірки різної довжини. Звідси й різний діапазон подання для різних типів дійсних чисел, хоча ідея зберігання майже та сама.

Формат float (single)

Ч исло це зберігається в комірці довжиною 32 біта, які розподіляються в такий спосіб:

Рис.4. Формат дійсного 32-бітного числа.

На Характеристику виділяються 8 бітів (розряди 23-30). Максимально можливе шістнадцяткове число, яке можна розмістити в цих бітах, дорівнює FFh, а його половина по визначенню — це Зсув = 7Fh.

ПРИКЛАД 4.

± l.0d → ± 1.0* 2⁰ b

Характеристика = 7F + 0 = 7F.

Розписуємо докладно вміст 32-х бітів, а потім переводимо двійкове подання в шістнадцяткове.

Позитивне число 1.0:

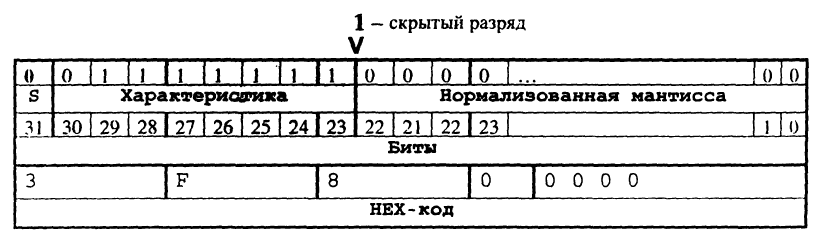
Рис.5. Формат дійсного 32-бітного числа 1.0 в Bin і Нех-Кодах

Негативне число -1.0 буде точно таке ж. тільки в знаковому біті S-1:

Рис. 6, Формат дійсного 32-бітного числа -1.0в Bin і Нех-Кодах.

Формат double

Рис. 7. Формат дійсного 64-бітного числа.

Тут ідея та ж сама, що й у попередньому форматі подання дійсних даних. На все число приділяється комірка довжиною 64 біта. На характеристику витрачаються 11 бітів (розряди 52-62). Максимально можливе число, яке можна розмістити в 11 -ти бітах: 111 1111 1111b. Звідси випливає, що

Зсув = 011 111 1 111 lb → 3FFh.

Мантиса теж має схований розряд. Таке подання дозволяє одержати наступний припустимий діапазон для даних типу double:

5.0 х 10^-324 .. 1.7 х 10^308

Формат long double (extended)

Рис. 8. Формат дійсного 80-бітного числа.

На все число приділяється 80 битов. Цей формат є основним робочим форматом для даних співпроцесора. Тому, щоб НЕ робити додаткових перетворень при обчисленнях, мантиса НЕ має схованого розряду. На характеристику витрачаються 15 бітів (розряди 64-78). Максимально можливе число, яке можна розмістити в 15-ти бітах: 111 1111 1111 111 Ib. Звідси випливає, що

Зсув = 011 1111 1111 1111b → 3FFFh.

Таке представлення дозволяє одержати наступний припустимий діапазон для даних цього типу: 3.6 х 10^-4951 .. 1.1 х 10^4932 і, відповідно, представити 19-20 десяткових цифр.

ПРИКЛАД 5

± 117.25d → ± 1.11010101* 2⁶b

Характеристика = 3FFF + 6 = 4005 (при додаванні ПОВНА аналогія з десятковою системою числення). Розписуємо наше число спочатку у двійковому коді, а потім у шістнадцятковому. В результаті одержуємо:

^{0 100 0000 0000 0101 1110 1010 1000 0000 ... 0000b}

117.25d → 4005ЕА80000000000000h

1 100 0000 0000 0101 1110 1010 1000 0000 ... 0000b

-117.25d →C005EA80000000000000h

4. Завдання для виконання лабораторної роботи.

1. Представити числа -3,56; 178,963; -D67F6,98FA у форматах дійсного 64-бітного та 80- бітного чисел.

5. Виконання лабораторної роботи.

1. Опрацювати теоретичні відомості.

2. Виконати поставлене завдання (п.4), записати результат.

3. Дати відповіді на контрольні питання(п.6).

4. Зробити висновки.

6. Контрольні питання.

1. Як представити дійсні числа в двійковому нормалізованому вигляді?

2. Опишіть структуру формату дійсного 32-бітного числа.

7. Зміст звіту.